🧐 Connected Components
그래프 $G$ 의 Connected Component 인 $G'$ 은 다음과 같이 정의됩니다.
Connected Component $G'$ of $G$ : Maximal connected subgraph of $G$
✔️ Maximum과 Maximal의 차이
Maximum : 최대를 의미합니다.
Maximal : 더이상 추가할 수 없는 상태를 의미합니다.
즉 Connected Component의 정의는 다음과 같이 해석 가능합니다.
$G'$ 에서 추가적으로 $G$ 에 존재하는 아무 정점 하나를 추가하는 순간 disconnected가 되며, $G'$ 은 가능한 모든 간선을 포함하고 있어야 합니다.
즉 induced subgraph를 의미합니다.
이제 Connected Component의 특성을 살펴보도록 하겠습니다.
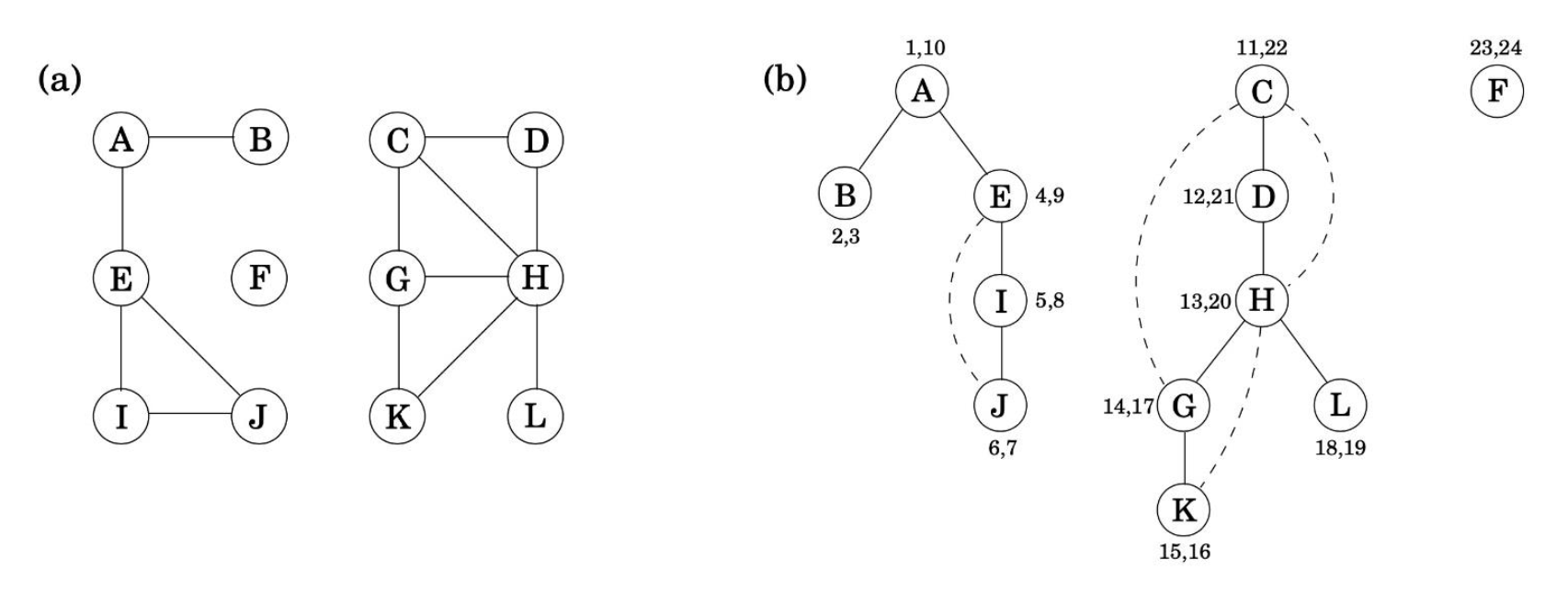
$G$ 의 connected component로 $G$ 의 vertex set(정점들의 집합)을 partitioning 할 수 있습니다.
또한 DFS forest를 이루는 각각의 DFS tree는 graph의 connected component에 대응합니다.
따라서 DFS 알고리즘 중 한번 explore를 호출할 때마다 새로운 connected component에 속한 vertex들을 모두 방문합니다.
이에 대한 증명은 reachablity 증명과 동일하며, 다음과 같습니다.
👉 증명
귀류법을 통해 증명하도록 하겠습니다.
'정점 $v$ 에서 explore를 호출할 때 $v$와 동일한 connected component에 속한 어떠한 vertex $u$ 를 방문하지 않는다'라고 가정하겠습니다.
$v$ 와 $u$ 는 같은 connected component에 속하므로, $v$ 와 $u$ 사이에는 Path가 존재합니다.
그리고 $v$ 와 $u$ 사이의 Path에 존재하는 정점들 중 마지막으로 방문한 정점을 $z$ 라 하겠습니다.
그리고 $z$ 이후에 바로 나오는 정점을 $w$ 라 가정하겠습니다.
explore procedure는 두 점 사이를 잇는 간선이 존재하면 반드시 방문 처리를 합니다.
그러나 $(z, w) \in E$ 임에도 불구하고, 방문하지 않으니 이는 $z$ 와 인접(adjacent)한 모든 정점을 방문한다는 사실에 모순됩니다.
따라서 한번 explore를 호출할 때마다 새로운 connected component에 속한 vertex들을 모두 방문합니다.
🧐 Articulation points (Cut Vertex)
그래프 $G$ 가 connected undirected graph라 하겠습니다.
어떤 $G$ 의 어떤 정점 $v$ 와, $v$ 와 연결된(incident) 모든 간선들을 제거할 경우,
$G$ 가 disconnected 된다면,
정점 $v$ 를 $G$ 의 articulation point ( cut vertex ) 라고 합니다.
예시 그림은 다음과 같습니다.
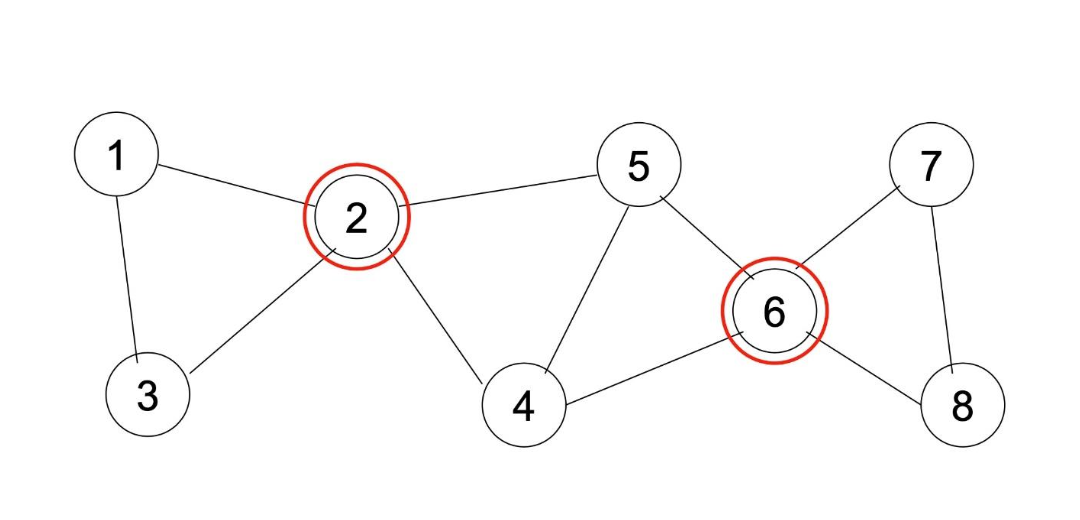
🧐 Articulation points 와 관련된 DFS Tree의 성질
✔️ 정리 1
DFS Tree의 Root Node의 Child Node가 2개 이상이라면,
root node는 articulation point이며, 그 역도 성립합니다.
👉 증명
첫번째 증명은 일반적인 케이스를 통한 증명입니다.
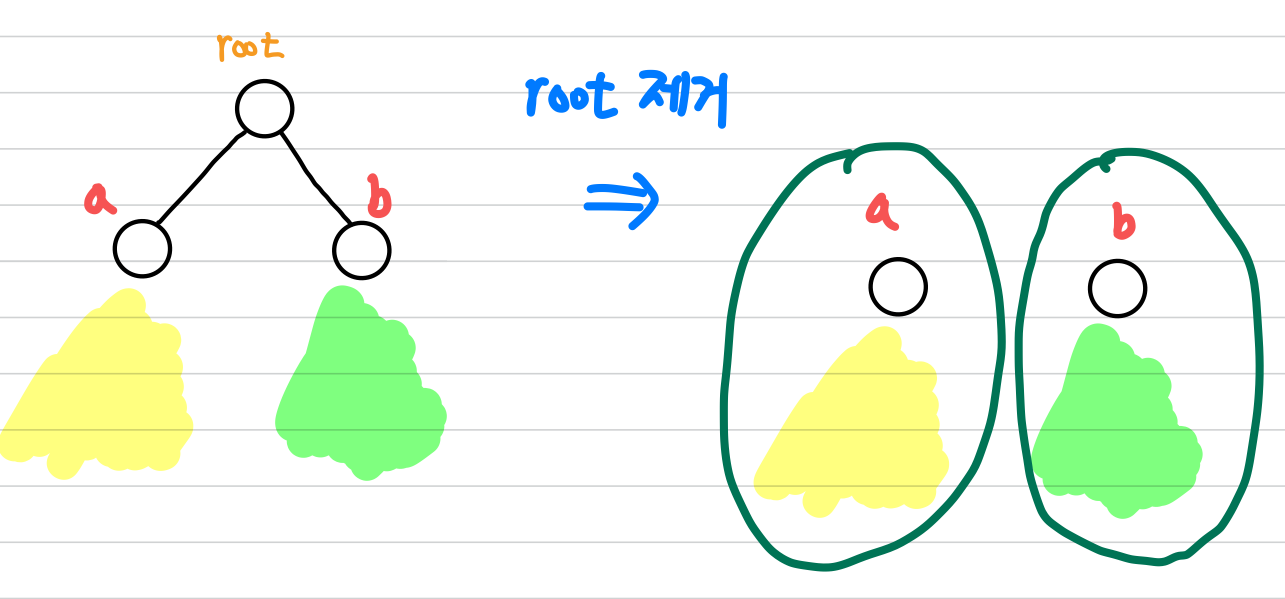
Root node $r$ 이, 두 자식(Children) $a, b$를 가진다고 하겠습니다.
만약 tree edge $(r, a)$ 와 $(r, b)$ 를 포함하는 cycle이 존재한다면, 둘 중 하나는 back edge가 되어야 하므로 모순됩니다.
따라서 root가 제거된다면 노드 $a$와 노드 $b$ 사이에는 path가 없으므로, 그래프 $G$ 는 disconnected가 됩니다.
즉 root node는 articulation point 입니다.
두번째 증명은 다음과 같습니다.
Root Node $r$ 을 Articulation Point라 하겠습니다.
그럼 Articulation Point의 정의에 의하여 DFS tree에서 $r$ 을 제거하면, 적어도 두개의 connected component가 생성되어야 합니다.
따라서 $r$ 의 child node는 두 개 이상이어야 합니다.
✔️ 정리 2
DFS Tree에서
i. $s$ 가 $v$ 의 child node이다.
ii. $s$ 의 descendant($s$를 포함한 자손)와 $v$의 proper ancestor($v$ 를 포함하지 않는 조상)를 연결하는 back edge가 존재하지 않는다.
위 두 조건을 모두 만족하는 두 루트 노드가 아닌 $v, s$ 가 존재할 경우, $v$는 articulation point 입니다.
👉 증명
첫번째 증명은 일반적인 케이스를 통한 증명입니다.
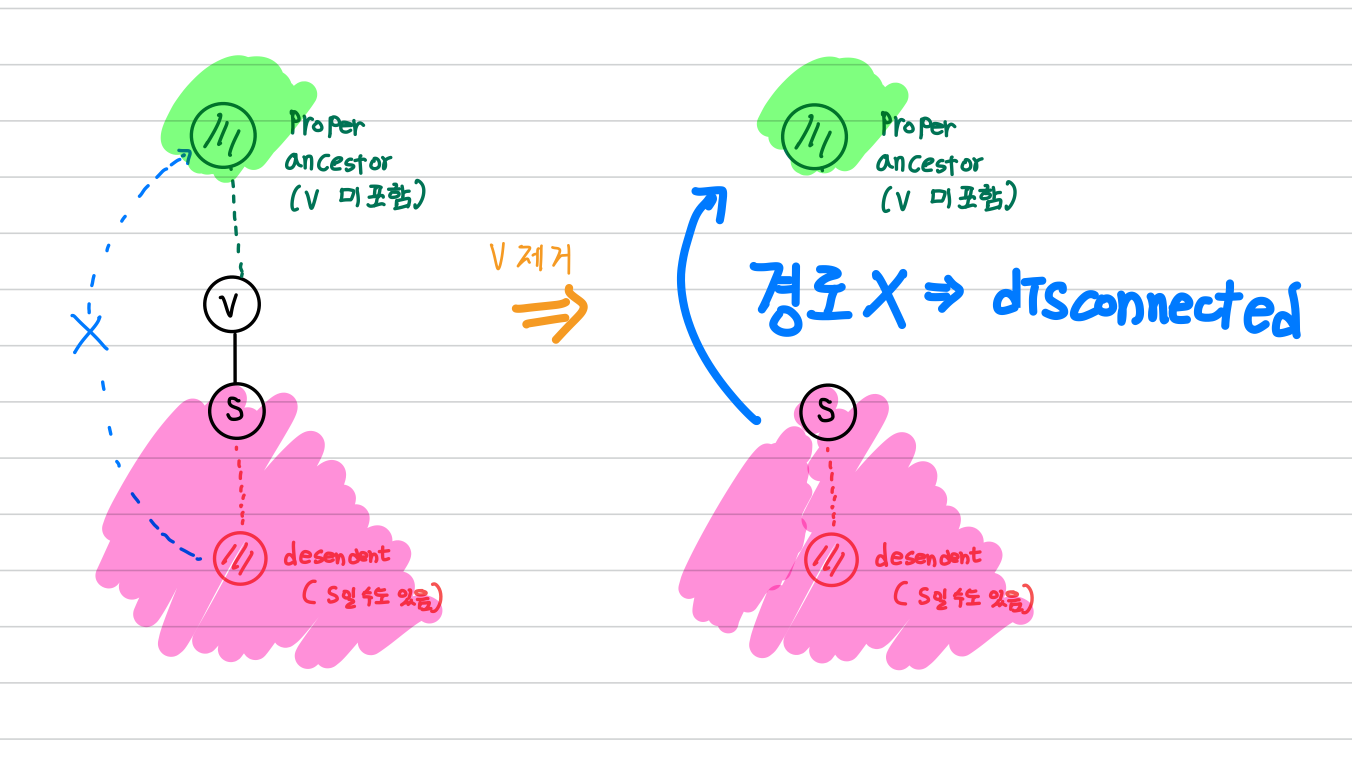
위 조건을 만족하는 node $s$ 가 있다고 하겠습니다.
그러면 $v$ 를 제거하면 $s$ 의 subtree 상의 어떠한 node도 해당 node에서 $v$ 의 proper ancestor로 가는 path가 존재하지 않게 됩니다.
(해당 path가 존재하기 위해서는 back edge가 필요하기 때문입니다.)
따라서 $v$ 는 articulation point 입니다.
두번째 증명은 다음과 같습니다.
위 조건을 만족하는 node $s$ 가 없다고 가정하겠습니다.
이 경우 $v$ 를 제거하더라도 $v$ 의 proper ancestor로 향하는 path가 존재합니다.
(back edge가 존재하므로)
따라서 $v$를 제거하더라도 그래프는 여전히 connected 합니다.
✔️ 정리 3
DFS Tree의 leaf node는 articulation point가 아닙니다.
👉 증명
Leaf node는 child node가 없기 때문에 해당 node를 제거해도 나머지는 여전히 tree 구조이며,
tree의 정의(Cycle이 없으며, Connected)에 의해 해당 그래프는 connected 합니다.
🧐 그래프의 Articulation Point 찾아내기 위한 성질
위에서 살펴본 DFS Tree의 3가지 성질을 이용합니다.
예시
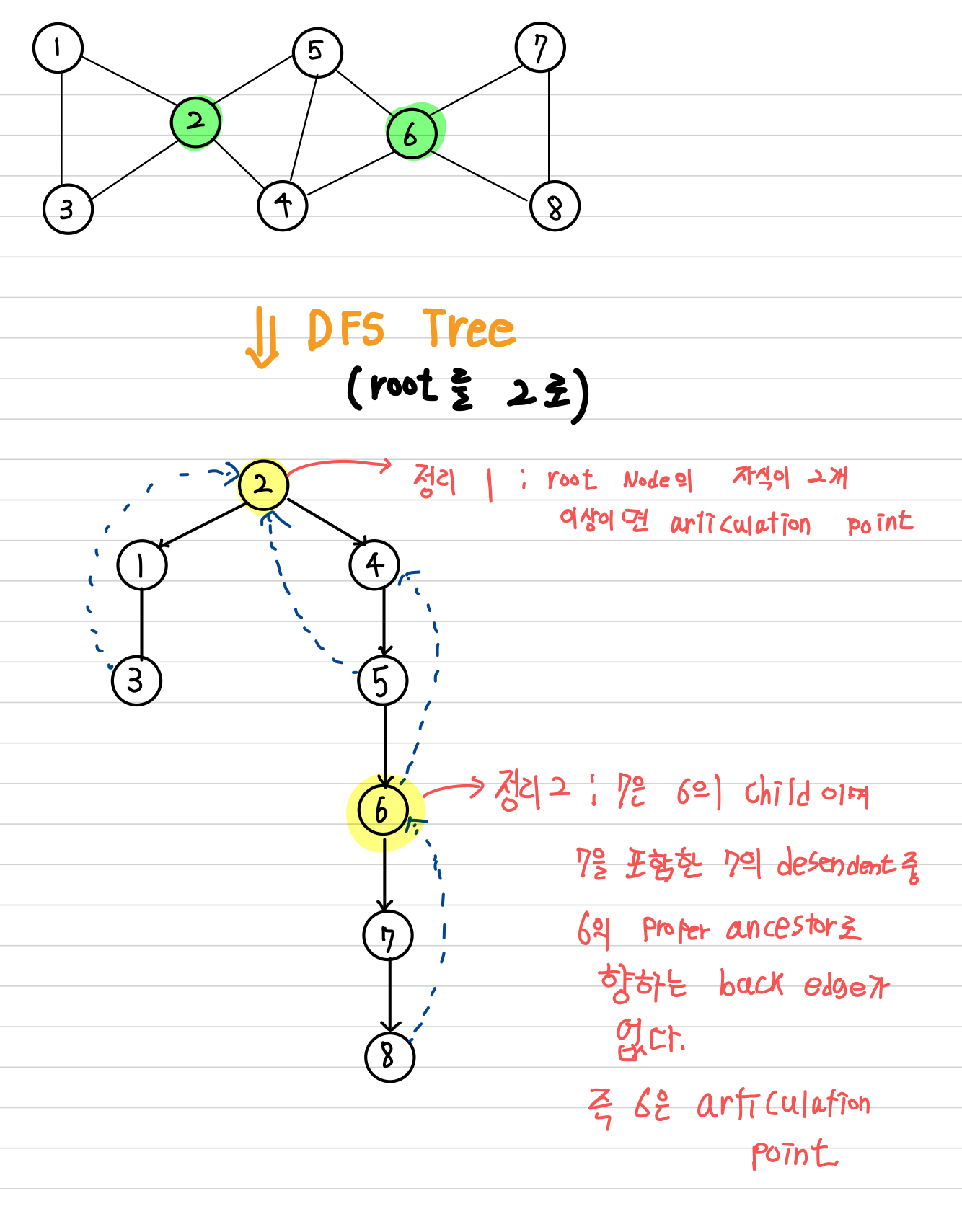
위의 방법을 코드상으로 구현하기 위해, previsit과 postvisit을 사용합니다.
구현에 필요한 성질은 다음과 같습니다.
DFS Tree의 어떠한 노드 $v$ 에 대하여,
$v$ 의 어떤 descendant($v$를 포함하는 자손) $u$ 와,
$u$ 와 incident한 back edge $(u, w)$ 가 있다면,
$low (v) = min(pre(v), pre(w))$ 로 정의하겠습니다.
(즉 $low(v)$ 는 $v$ 에서 도달 가능한 가장 pre가 낮은 노드의 pre값을 의미합니다.)
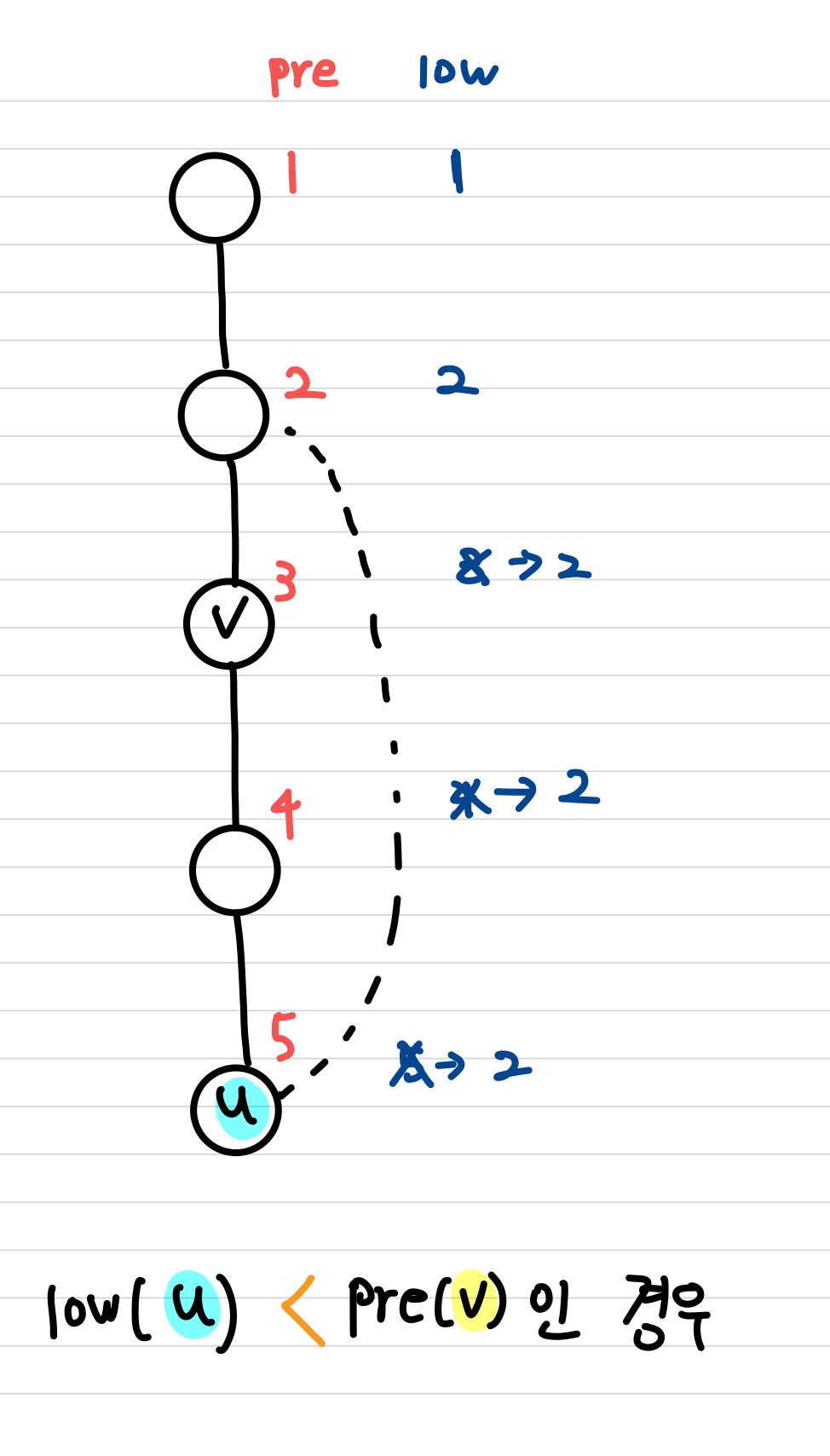
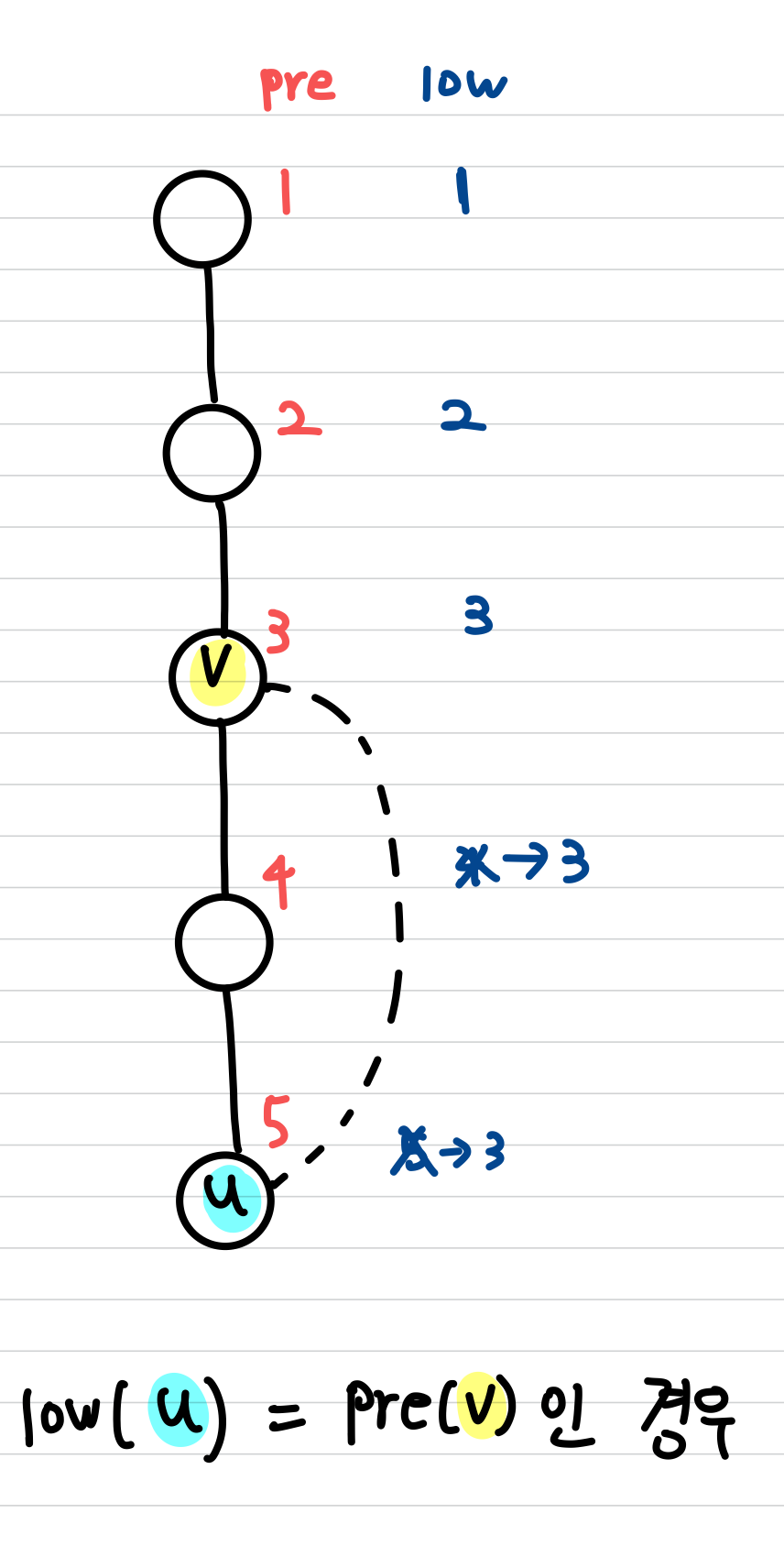
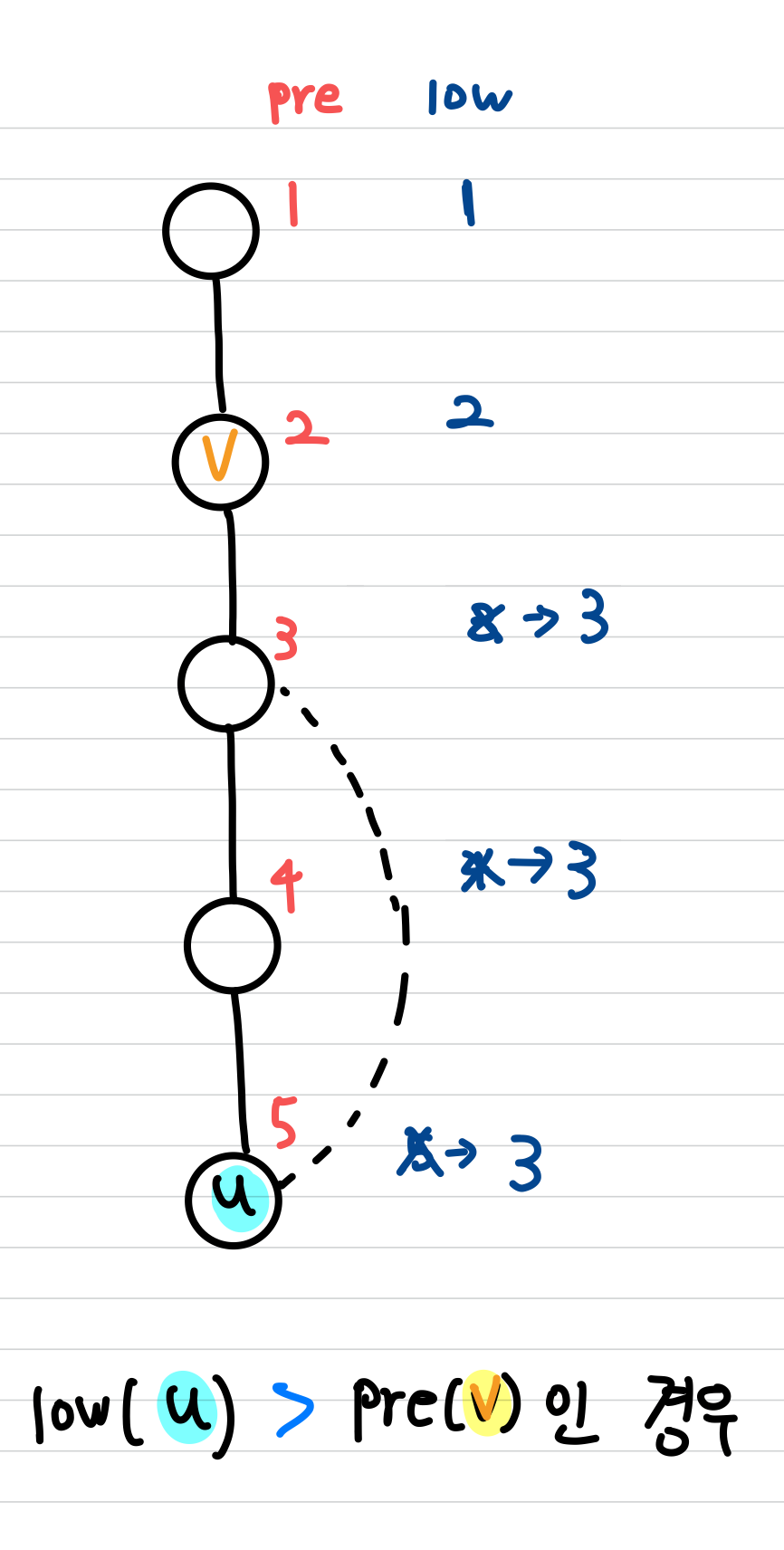
이때 루트 노드가 아닌 $v$ 가 $low(u)$ $\geq$ $pre(v)$ 를 만족하는 자식(child) 노드 $u$ 를 가지고 있다면, $v$ 는 articulation point이며, 역도 성립합니다.
이때 Articulation Point를 판별하기 위해 비교하는 노드는 자손 노드가 아닌 자식 노드만 비교함에 주의해야 합니다.
👉 증명

아래는 귀류법에 의한 증명입니다.
루트 노드가 아닌 $v$ 에 대하여, $low (u) \geq pre(v)$ 를 만족하는 child node $u$ 를 가지고 있을 때 $v$가 Articulation point가 아니라 가정해 보도록 하겠습니다.
$low (u) \geq pre(v)$ 이기 때문에 $u$의 desendent 에서 $v$ 의 proper ancestor로의 back edge가 존재하지 않습니다.
따라서 v를 제거한다면 v의 proper ancestor로의 path가 없어지므로 그래프는 disconnected 됩니다.
따라서 $v$ 는 Articulation point가 아니라는 가정이 모순입니다.
$low(u)$ 는 DFS Tree 상에서 $v$ 와 $v$ 의 Descendant들( $v$ 포함 )와 연결된 요소들 중에서,
간선 하나를 사용하여 도달 가능한 preOrder 값이 가장 작은 정점을 의미합니다.
이제 이를 이용하여 그래프 내의 모든 Articulation Point를 찾는 알고리즘을 살펴보겠습니다.
🧐 그래프 내의 모든 Articulation Point 찾아내는 알고리즘
- 루트 노드의 경우 '정리 1' 을 통해 쉽게 알아낼 수 있습니다. (child node가 2개 이상 있는지만 확인)
- 루트 노드가 아닌 경우
- DFS 를 수행하며 low 값을 계속 업데이트합니다.
- 만약 정점 $v$ 의 자식 노드 $u$ 에 대한 explore 가 끝난 뒤, $pre(v)$ 와 $low(u)$ 를 비교하여, $low(u)$ $\geq$ $pre(v)$ 인 경우, $v$ 는 Articulation Point 입니다.
DFS 도중 $low(v)$ 를 업데이트 하는 방법
초기 $low(v)$ 의 값은 $pre(v)$ 입니다.
이후 DFS를 수행하며, Back edge $(v, u)$ 가 있다면, $low(v)$ $=$ $min(\;$ $low(v)$ $,$ $pre(u)$ $\;)$ 로 업데이트 합니다.
$v$의 자식(child) $u$ 에 대한 explore가 끝나면 $low(v)$ $= min(\;$ $low(v)$ $,$ $low(u)$ $\;)$ 로 업데이트합니다.
수도코드

코드로 구현
다음 그래프에 대해 코드로 구현해 보도록 하겠습니다.
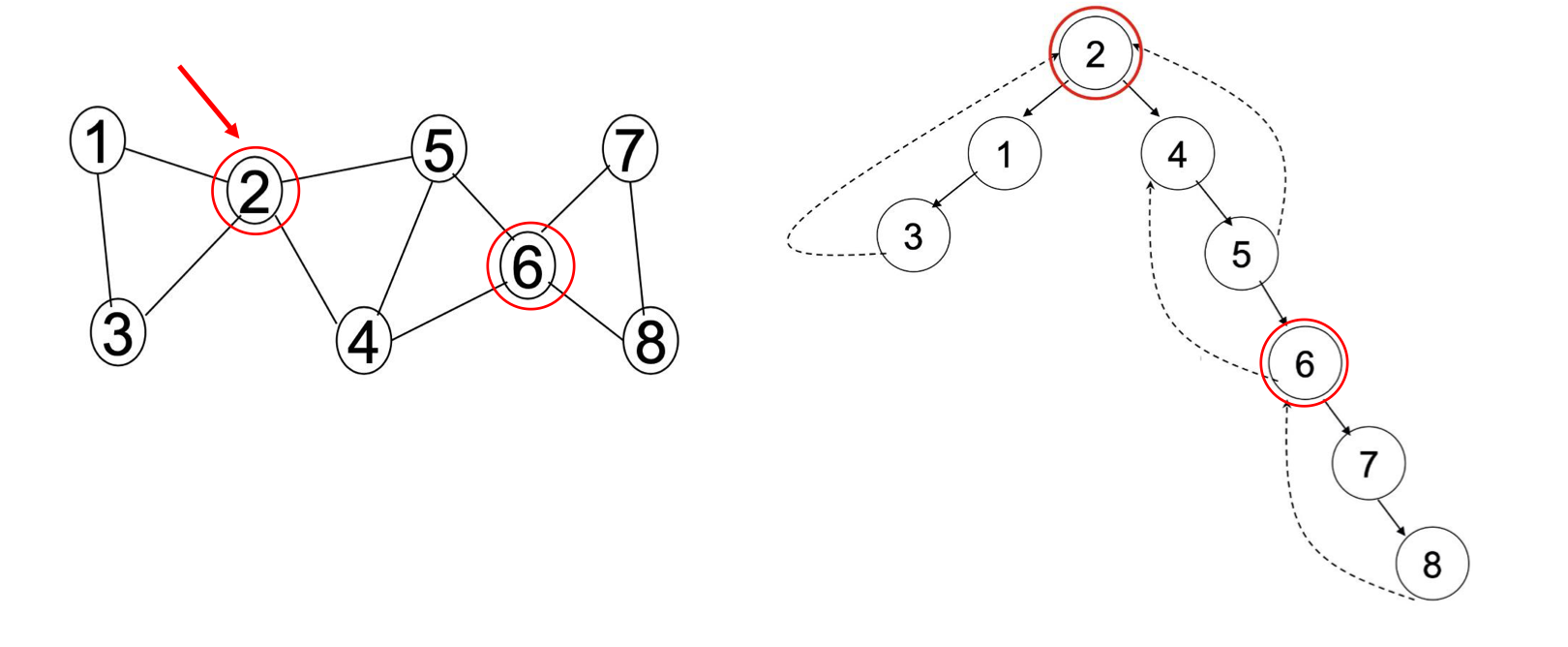
/**
* Created by ShinD on 2022/09/22.
*/
fun main() {
val graph = GraphMaker().make()
GraphExplorer().findCutPoint(
graph = graph,
current = GraphMaker.b,
root = GraphMaker.b
)
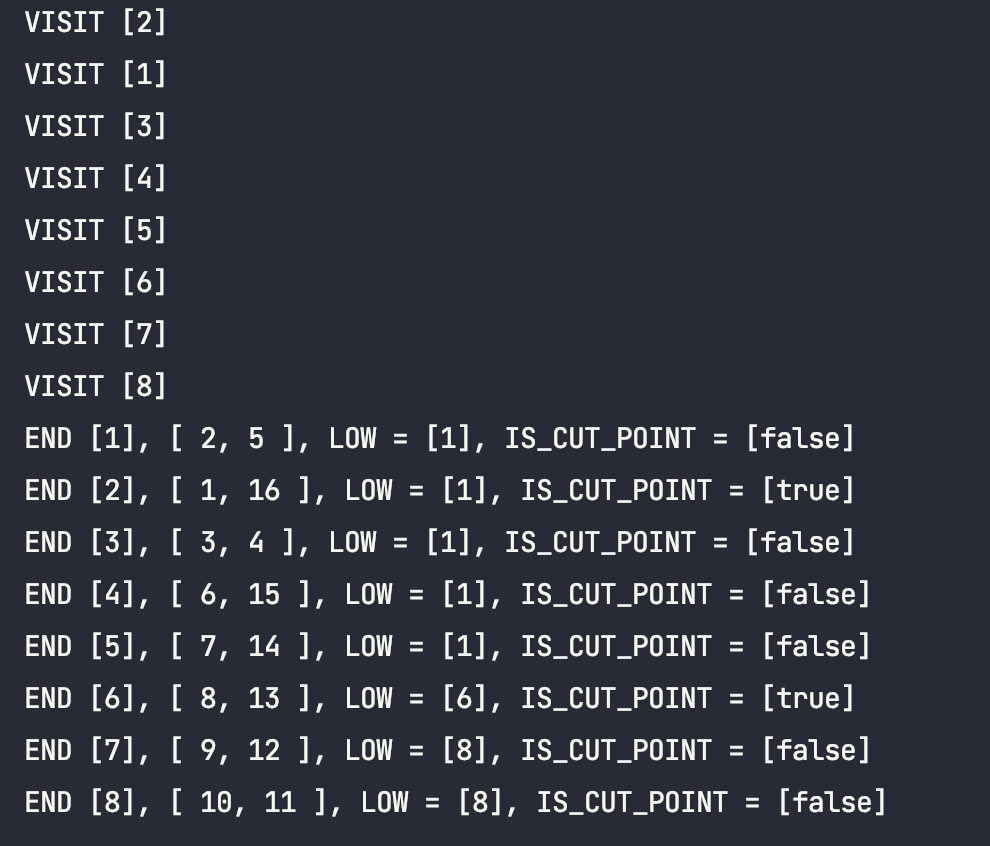
GraphMaker.vertexSet().forEach {
println("END [${it.value}], [ ${it.preOrder}, ${it.postOrder} ], LOW = [${it.low}], IS_CUT_POINT = [${it.isCutPoint}]")
}
}
class Graph(
val vertexSet: Set<Vertex>,
val graph: List<List<Vertex>>,
)
class GraphMaker {
companion object {
val a = Vertex('1')
val b = Vertex('2')
val c = Vertex('3')
val d = Vertex('4')
val e = Vertex('5')
val f = Vertex('6')
val g = Vertex('7')
val h = Vertex('8')
fun vertexSet(): Set<Vertex> {
return setOf(
a, b, c, d, e, f, g, h,// i, j, k, l
)
}
}
fun make(): Graph {
return Graph(
vertexSet = vertexSet(),
graph = listOf(
listOf(b, c), // 1
listOf(a, c, d, e), // 2
listOf(a, b), // 3
listOf(b, e, f), // 4
listOf(b, d, f), // 5
listOf(d, e, g, h), // 6
listOf(f, h), // 7
listOf(f, g), // 8
)
)
}
}
class Vertex(
val value: Char,
var preOrder: Int = 0,
var postOrder: Int = 0,
var low: Int = 0,
var isVisited: Boolean = false,
var isCutPoint: Boolean = false,
)
class GraphExplorer {
// 시작 전 1로 초기화
private var counter = 1
private fun visited(vertex: Vertex) {
vertex.isVisited = true
println("VISIT [${vertex.value}]")
}
private fun preVisit(vertex: Vertex) {
vertex.preOrder = counter
counter++
}
private fun postVisit(vertex: Vertex) {
vertex.postOrder = counter
counter++
}
fun findCutPoint(
graph: Graph, // Connected Graph
current: Vertex, // DFS 진행할 Vertex
root: Vertex, // DFS 를 처음 진행한 Root Vertex
parent: Vertex? = null,
) {
val idx = current.value - '1'
// 방문 처리
visited(current)
// preVisit
preVisit(current)
// PreOrder 값으로 low 설정
current.low = current.preOrder
var children = 0
// 루트 vertex와 adjacent 한 모든 vertex 탐색
graph.graph[idx].forEach { vertex ->
// Back Edge인 경우
if (vertex.isVisited && vertex != parent) {
current.low = Math.min(current.low, vertex.preOrder)
}
// 아직 방문하지 않았다면 explore
if (!vertex.isVisited) {
findCutPoint(graph, vertex, root, current)
current.low = Math.min(current.low, vertex.low)
if (
current != root // 이때 current는 root가 아니어야 함
&& vertex.low >= current.preOrder // 자식 노드(vertex) 에서 현재 노드(current)의 proper ancestor로 향하는 Back Edge가 없는 경우
) {
current.isCutPoint = true; // current는 Articulation Point(Cut Point)
}
// 자식 수 1 증가
children++
}
}
// 만약 루트노드이며, 자식 수가 2개 이상인 경우
if ((current.value == root.value) && children > 1) {
current.isCutPoint = true
}
postVisit(current)
}
}
백준 문제
아래 문제는 단절점(Articulation Point)을 찾아내는 알고리즘을 이해하셨다면, 풀어낼 수 있는 문제입니다.
https://www.acmicpc.net/problem/11266
11266번: 단절점
첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B
www.acmicpc.net
아래와 같은 방법도 있습니다.
바로 Articulation Point의 정의를 통한 방법으로, 다음과 같은 과정을 통해서 찾아냅니다.
그래프에서 정점들을 하나씩 제거해가며 앞에서 살펴본 DFS를 사용하여 연결성(Connectivity)을 체크합니다.
해당 과정에서, 어떠한 정점 $v$ 가 제거된 후 그래프 $G$ 가 disconnected 상태가 된다면, $v$ 는 Articulation Point가 되는 것입니다.
그러나 해당 알고리즘은 앞서 살펴본 알고리즘에 비해 시간 복잡도가 훨씬 높으므로 좋은 알고리즘이 아닙니다.
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 (5) - Directed Graph 에서의 DFS (0) | 2022.09.24 |
|---|---|
| [알고리즘] 그래프 (4) - 이중 연결 요소 (Biconnected Components) (0) | 2022.09.24 |
| [알고리즘] 그래프 (2) - DFS (0) | 2022.09.24 |
| [알고리즘] 그래프 (1) - 그래프의 기본 용어 (0) | 2022.09.24 |
| [알고리즘] Selection 알고리즘 (0) | 2022.09.19 |
