-
🧐 그래프 (Graph)
-
🧐 Simple Graph
-
🧐 Directed Graph와 Undirected Graph
-
🧐 Adjacent
-
🧐 Degree (차수)
-
-
🧐 Subgraph (부분 그래프)
-
🧐 Walk(보행), Trail, Path(경로), Circuit(회로 ), Cycle(순환)
-
✔️ Walk(보행)
-
✔️ Trail
-
✔️ Path(경로)
-
🐛암기 Tip
-
✔️ Circuit(회로)
-
✔️ Cycle(순환)
-
예시
-
🧐 Connected Graph
-
🧐 그래프와 시간복잡도
-
🧐 Reachability (접근 가능성)
-
🧐 Reachability 알고리즘
-
🖥 코드로 구현
-
🧐 previsit, postvisit는 뭐예요??
-
🧐 어따 쓰는데요???
🧐 그래프 (Graph)
그래프는 정점(vertex)들과 간선(edge)들로 이루어진 구조로써, 기호로는 다음과 같이 표현합니다.
$$G = (V(G), E(G))$$
$V$ 는 정점을, $E$ 는 간선을 의미합니다.
🧐 Simple Graph
Self loop 또는 Multiple Edge를 가지지 않는 그래프를 Simple Graph라고 합니다.
그림으로는 아래와 같습니다.
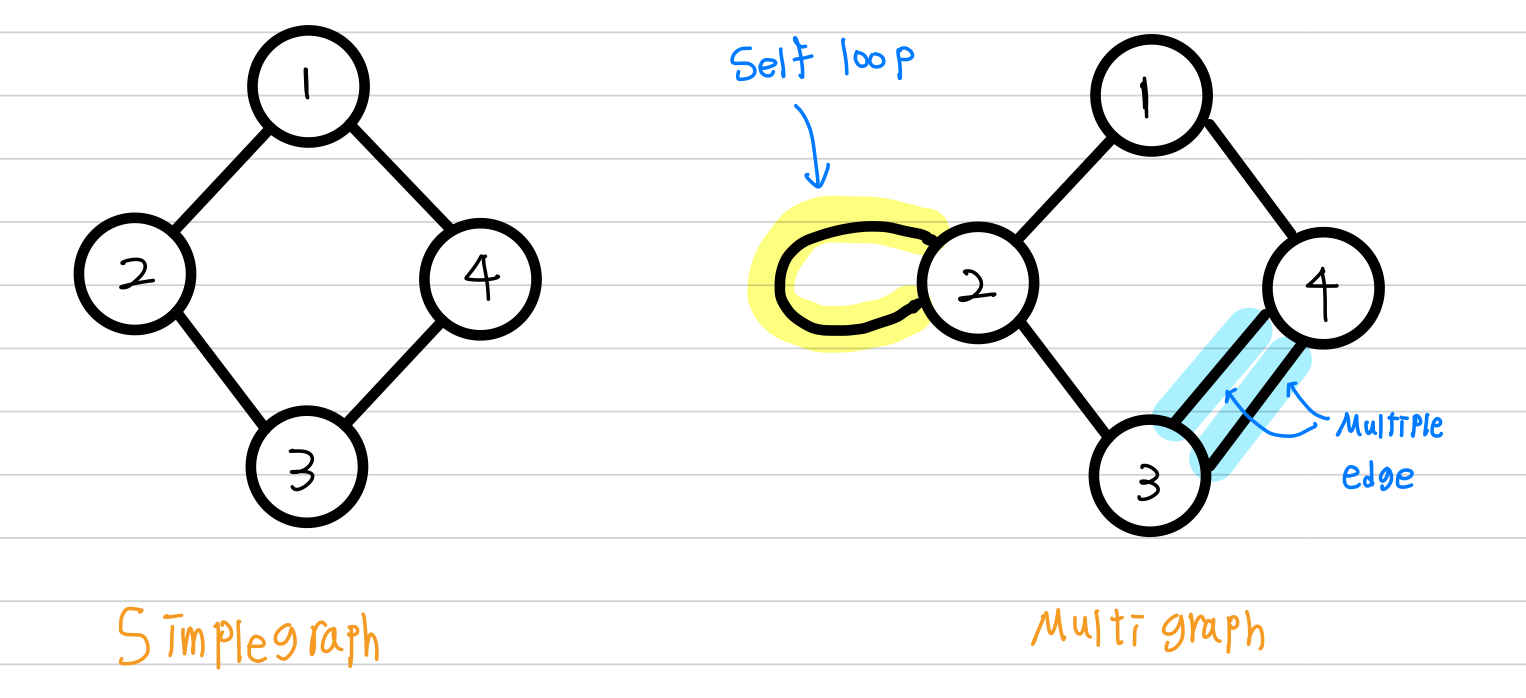
앞으로 등장하는 모든 그래프는, 특별한 설명이 없는 이상 Simple Graph라고 가정하겠습니다.
🧐 Directed Graph와 Undirected Graph
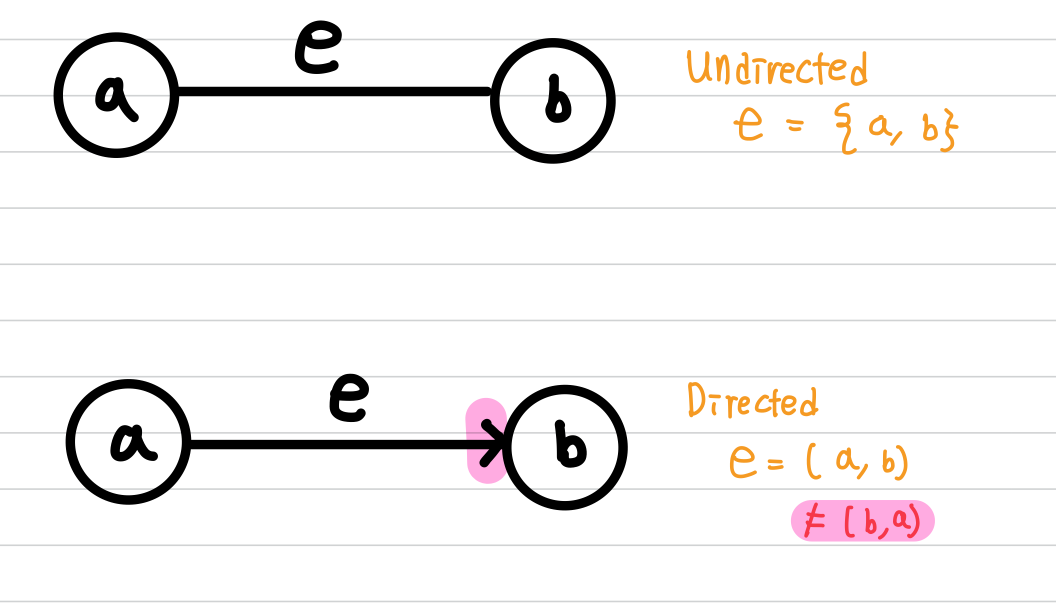
그래프에 속한 $E$ (간선)의 각 원소들이 ordered pair 즉 방향성이 있는 경우, 해당 그래프를 방향 그래프(Directed Graph)라고 합니다.
반대로 $E$ (간선)의 각 원소들이 unordered pair 즉 방향성이 없는 경우, 해당 그래프를 무방향 그래프(Undirected Graph)라고 합니다.
🧐 Adjacent
두 정점 $v,\; u$ 에 대하여 $(v, u)\in E$ 일 때, 즉 두 정점을 잇는 간선이 존재하는 경우,
$v$ 는 $u$ 와 adjacent(인접하다)라고 표현합니다.
Undirected Graph의 경우 $v$ 와 $u$ 가 adjacent 하다면, $v$ 와 $u$ 역시 adjacent 입니다.
🧐 Degree (차수)
어떠한 정점 $v$ 에 대한 차수(degree)는 그래프 $G$ 에서 $v$ 와 adjacent한 정점의 수를 의미합니다.
Directed Graph의 경우 in-degree와 out-degree를 따로 정의하여 사용하지만, 고려하지 않고 넘어가도록 하겠습니다.
🧐 Subgraph (부분 그래프)
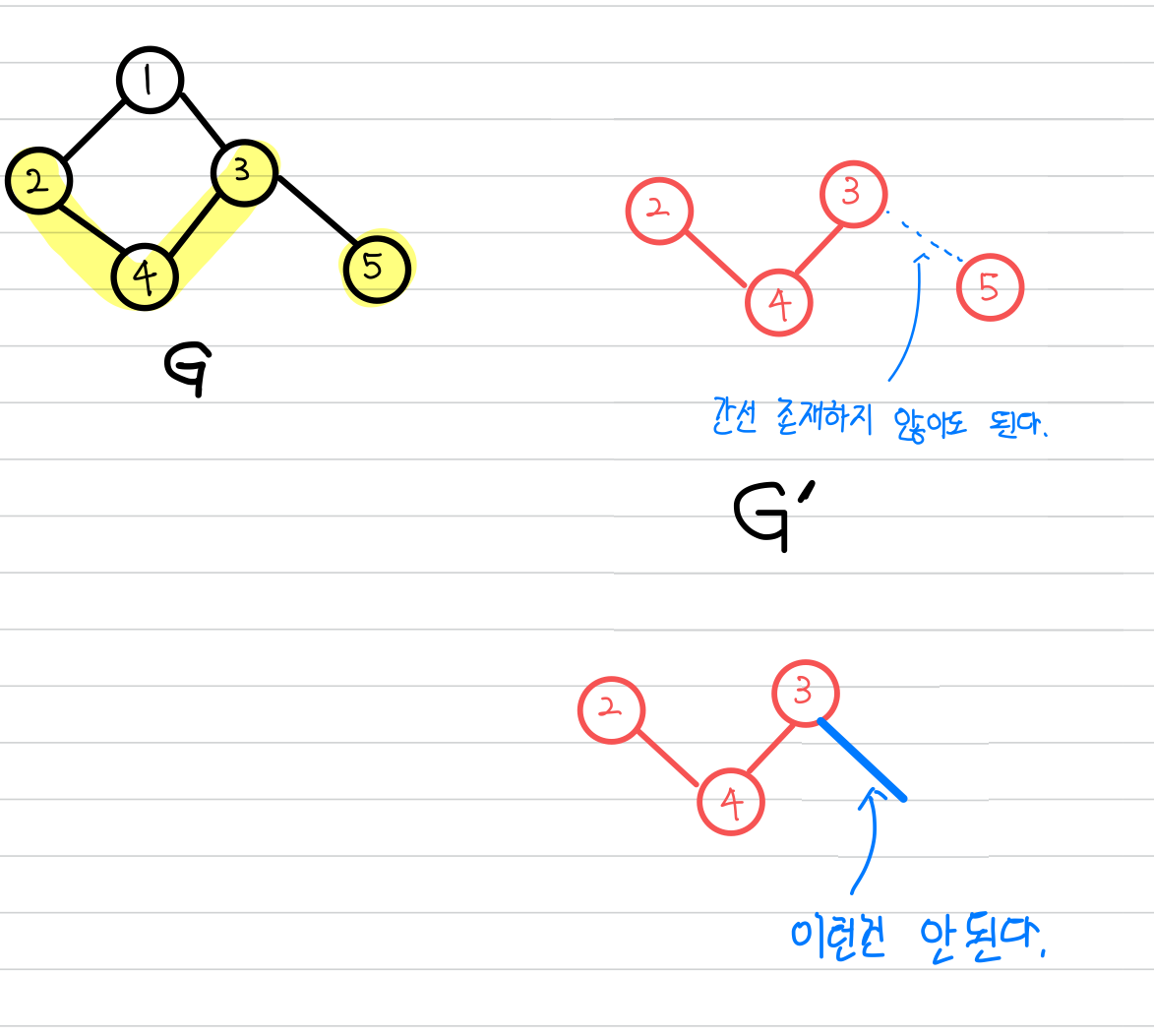
그래프 $G = (V(G), E(G))$ 에서 그래프 $G$ 의 subgraph $G' = (V(G'), E(G'))$ 는 다음과 같은 조건을 만족합니다.
1. $V(G') \subseteq V(G)$ : 서브그래프 $G'$ 에 속하는 정점들의 집합은, 그래프 $G$ 의 정점들의 부분집합이어야 합니다.
2. $E(G') \subseteq E(G) $ : 서브그래프 $G'$ 에 속하는 간선들의 집합은, 그래프 $G$ 의 간선들의 부분집합이어야 합니다.
3. $E(G')$ 에 속하는 모든 간선들은 $V(G')$ 의 정점들만을 사용해야 합니다.
예시는 아래와 같습니다.
🧐 Walk(보행), Trail, Path(경로), Circuit(회로 ), Cycle(순환)
(해당 부분의 정의들은 책마다 다르게 정의될 수 있으며, 저는 제가 참고하는 책을 기준으로 정리한 것입니다.)
✔️ Walk(보행)
그래프에 속한 두 정점을 골랐을 때, 두 정점이 어떻게든 연결되어 있다면 두 정점 사이에 보행이 존재한다고 표현합니다.
정의는 다음과 같습니다.
$v_1$ , $e_1$ , $v_2$ , $e_2$ , ..., $e_k$ , $v_k$ 로 이어지는,
정점 $v_1, \; v_2, \; ...$ 과 간선 $e_1, \; e_2\; ..$ 가 서로 교차되며 나타나는 sequence(혹은 alternating sequence)를 의미합니다.
정점 사이를 이동하기 위해서는 간선이 반드시 필요하므로, 어찌보면 당연한 정의일 수 있습니다.
보행(Walk)은 정점과 간선이 교차되야 한다는 것 외에는 제약조건이 존재하지 않습니다.
앞으로 나오는 개념들은 보행에 추가적인 제약조건이 걸린 개념들입니다.
✔️ Trail
제약조건: 같은 간선(Edge)이 두 번 이상 반복되면 안됩니다.
제약조건을 통한 Trail의 정의는 다음과 같습니다.
같은 간선(Edge)이 두 번 이상 반복되지 않는 Walk(보행)을 의미합니다.
✔️ Path(경로)
제약조건: 같은 정점(Vertex)이 두 번 이상 반복되면 안됩니다.
제약조건을 통한 Path의 정의는 다음과 같습니다.
같은 정점(Vertex)이 두 번 이상 반복되지 않는 Walk(보행)을 의미합니다.
Undirected Graph에서는 Path인 경우 Trail를 만족하지만, 그 역은 성립하지 않습니다.
(8자를 그린다고 생각해보세요)
🐛암기 Tip
트패는 애벌래
- 트(Trail) - 애(Edge)가 반복되지 않음
- 패(Path) - 벌(Vertex)가 반복되지 않음
✔️ Circuit(회로)
제약조건:
같은 간선(Edge)이 두 번 이상 반복되지 않으며,
시작 정점(Vertex)과 마지막 정점이 동일해야 합니다.
제약조건을 통한 Circuit(회로)의 정의는 다음과 같습니다.
같은 간선(Edge)이 두 번 이상 반복되지 않고, 시작 정점(Vertex)과 마지막 정점이 동일한 Walk(보행)를 의미합니다.
이는 다음과도 같습니다.
시작 정점(Vertex)과 마지막 정점이 동일한 Trail을 의미합니다.
✔️ Cycle(순환)
제약조건:
같은 간선(Edge)이 두 번 이상 반복되지 않으며,
시작 정점(Vertex)과 마지막 정점이 동일해야 하고,
이 두 정점을 제외한 나머지 정점들은 두 번 이상 반복되지 않아야 합니다.
제약조건을 통한 Cycle(순환)의 정의는 다음과 같습니다.
같은 간선(Edge)이 두 번 이상 반복되지 않고,
시작 정점(Vertex)과 마지막 정점이 동일하며,
이외 나머지 정점들은 두 번 이상 반복되지 않는 Walk(보행)를 의미합니다.
이는 다음과도 같습니다.
시작 정점(Vertex)과 마지막 정점이 동일하며, 이외 나머지 정점은 반복되지 않는 Trail을 의미합니다.
시작 정점(Vertex)과 마지막 정점을 제외하고 같은 정점이 두 번 이상 반복되지 않는 Circuit(회로)을 의미합니다.
예시
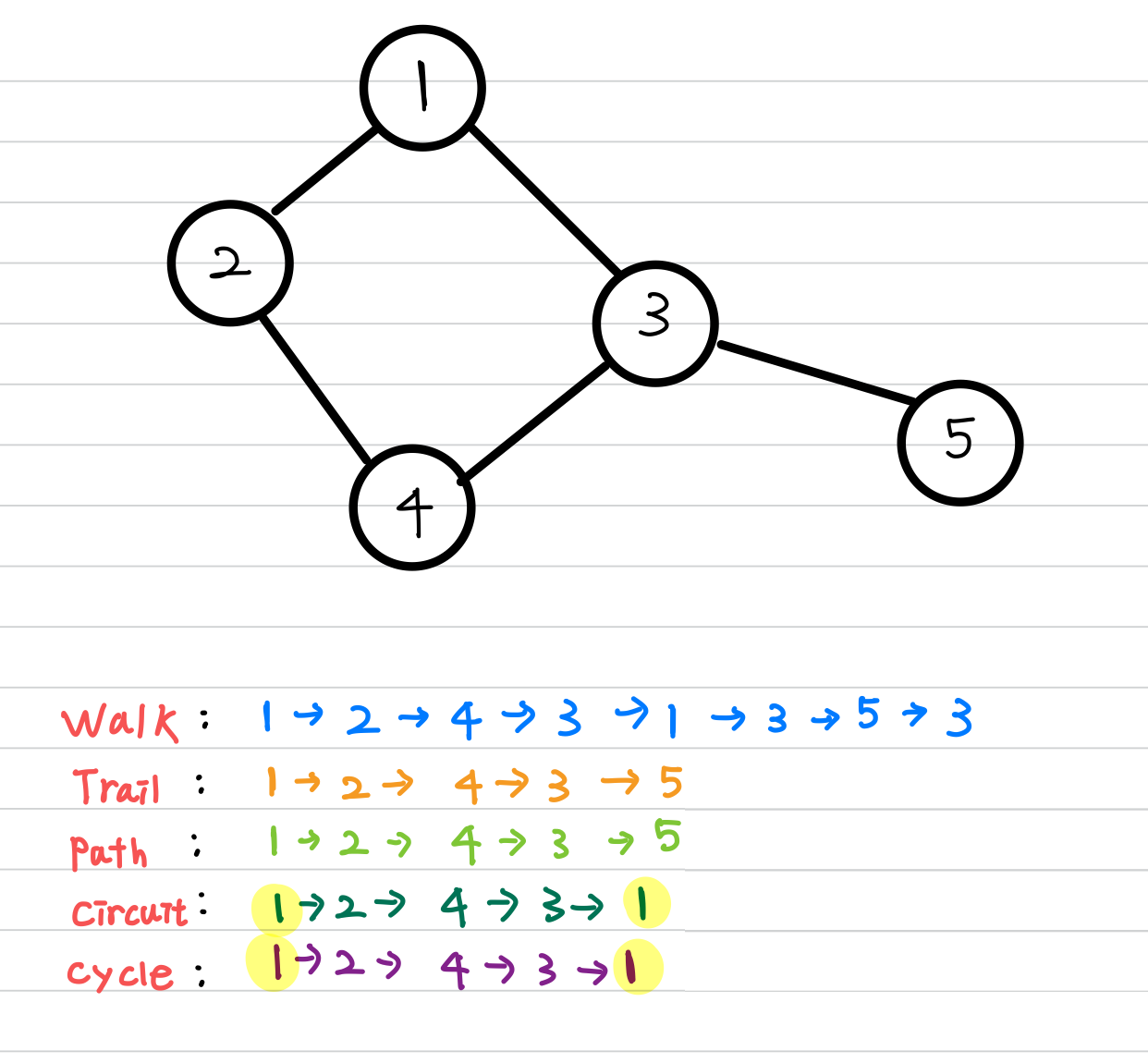
🧐 Connected Graph
(Directed Graph의 경우는 뒤에서 따로 정의하도록 하겠습니다.)
Undirected Graph $G = (V, E)$ 에서 다음 조건을 만족하는 경우 그래프 $G$ 를 Connected Graph라 표현합니다.
임의의 서로 다른 두 정점(vertex) $v, w \in V$ 에 대하여, $v$ 에서 $w$ 로의 path가 존재합니다.
이 경우 G는 Connected 하다고도 표현합니다.
임의의 두 정점을 고르는 것이므로, 그래프에 존재하는 모든 점에 대해서 서로간의 path가 존재해야 하는 것입니다.
Connected 하지 않은 그래프는 disconnected(비연결)라고 합니다.
🧐 그래프와 시간복잡도
그래프를 코드 상으로 표현하는 방법에는 배열을 사용하는 방법과 리스트를 사용하는 방법이 있습니다.
리스트는 조금 헷갈릴 수도 있으므로, 이해를 돕기 위해 사진을 추가하겠습니다.
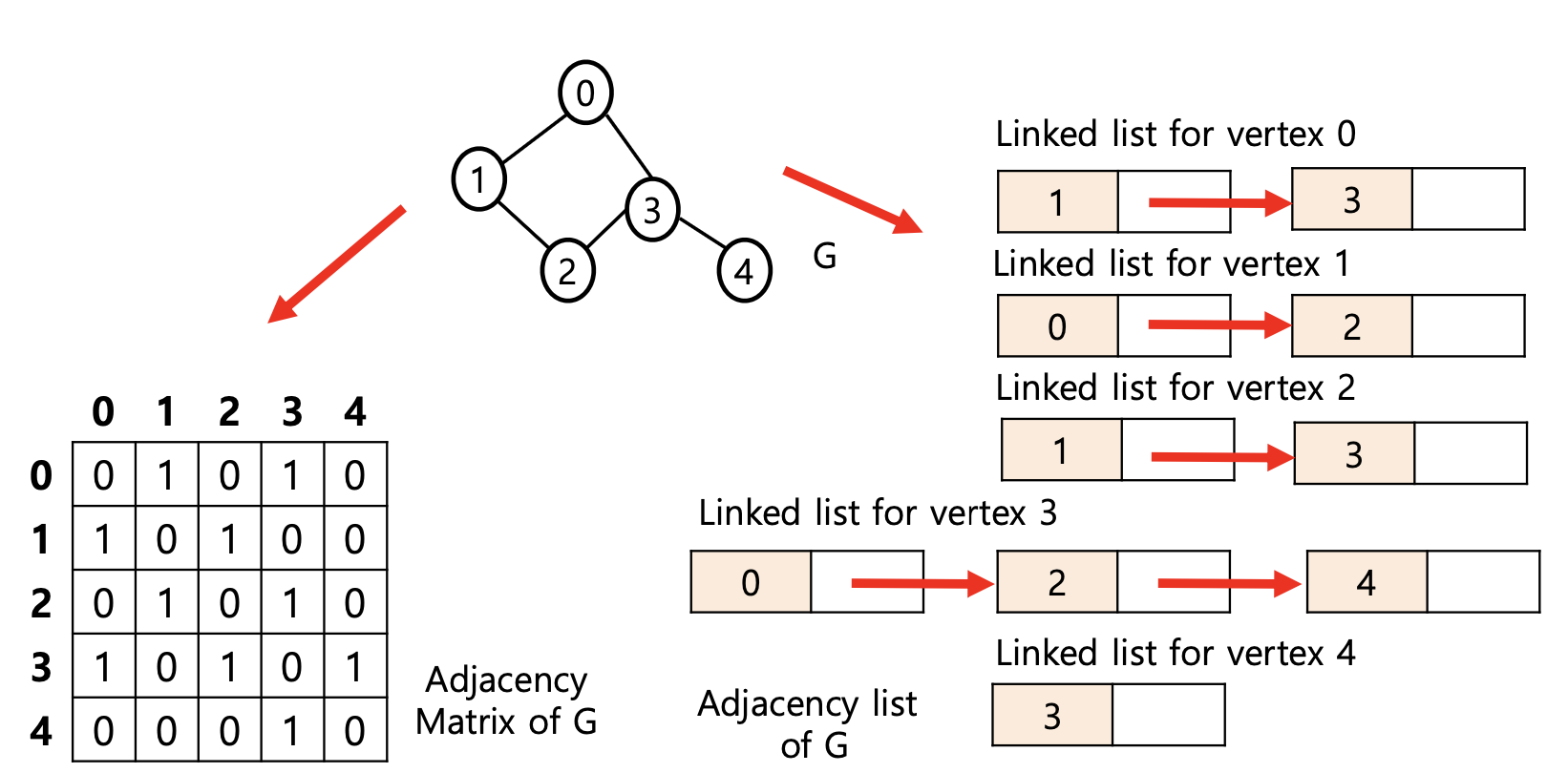
그래프에서 행해질 수 있는 여러 연산들에 대하여, 두 방법간의 시간 복잡도 차이를 알아보도록 하겠습니다.
| 배열에 저장 | 리스트에 저장 | |
| 공간(Space) | $O(n^{2})$ | $O(n + m)$ |
| 정점 $u$ 와 $v$ 가 인접(adjacent)한지 확인 | $O(1)$ | $O(deg(u))$ |
| 정점 $u$ 와 인접(adjacent)한 모든 정점 확인 | $O(n)$ | $O(deg(u))$ |
| 정점 $u$ 의 차수 구하기 | $O(n)$ | $O(deg(u))$ |
이제부터 나오는 알고리즘에 대해서는, 모두 list에 저장되어 있다고 가정하도록 하겠습니다.
🧐 Reachability (접근 가능성)
Undirected graph $G$ 의 두 정점(vertex) $u$, $v$ 에 대하여,
정점 $u$ 에서 $v$ 로의 path가 있으면,
$v$ 는 $u$ 로부터 reachable(접근 가능한)이라고 합니다.
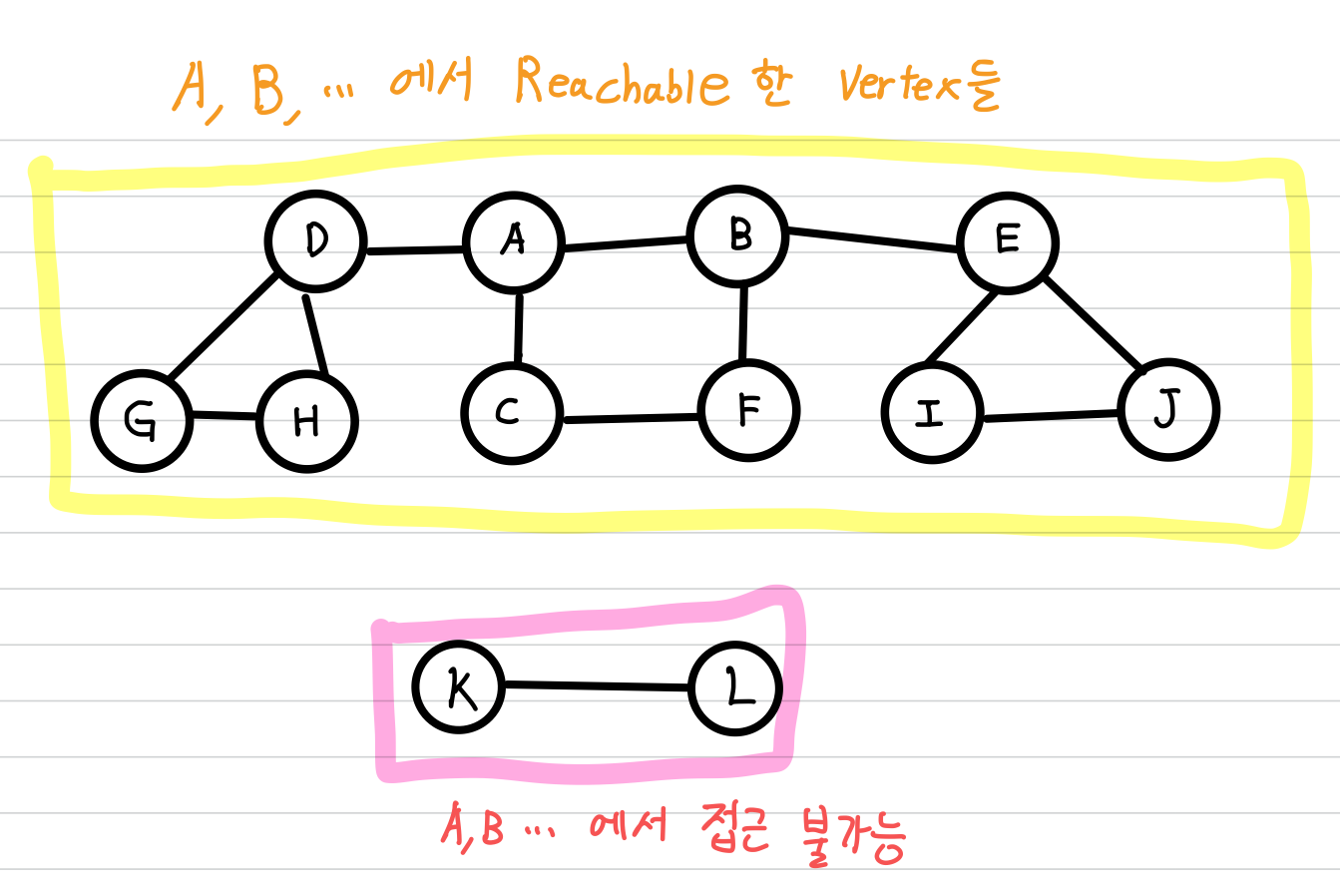
🧐 Reachability 알고리즘
어떠한 정점 $v$ 에서 reachable한 모든 정점들을 찾는 알고리즘은 다음과 같습니다.

해당 알고리즘이 올바르게 동작함은 다음과 같이 증명할 수 있습니다.
👉 증명
증명하고자 하는 정리(Theorem)는 다음과 같습니다.
explore($G, \;v$)는 올바르게 동작한다.
증명은 귀류법(Proof by Contradiction)을 통해 진행됩니다.
'explore($G, \; v$) 가 v에서 reachable한 어떤 정점 $u$ 를 방문하지 않는다'고 가정하겠습니다.
그리고 $v$ 와 $u$ 사이의 Path에 존재하는 정점들 중 마지막으로 방문한 정점을 $z$ 라 하겠습니다.
그리고 $z$ 이후에 바로 나오는 정점을 $w$ 라 가정하겠습니다.
(이해를 돕기 위한 그림으로는 다음과 같습니다.)
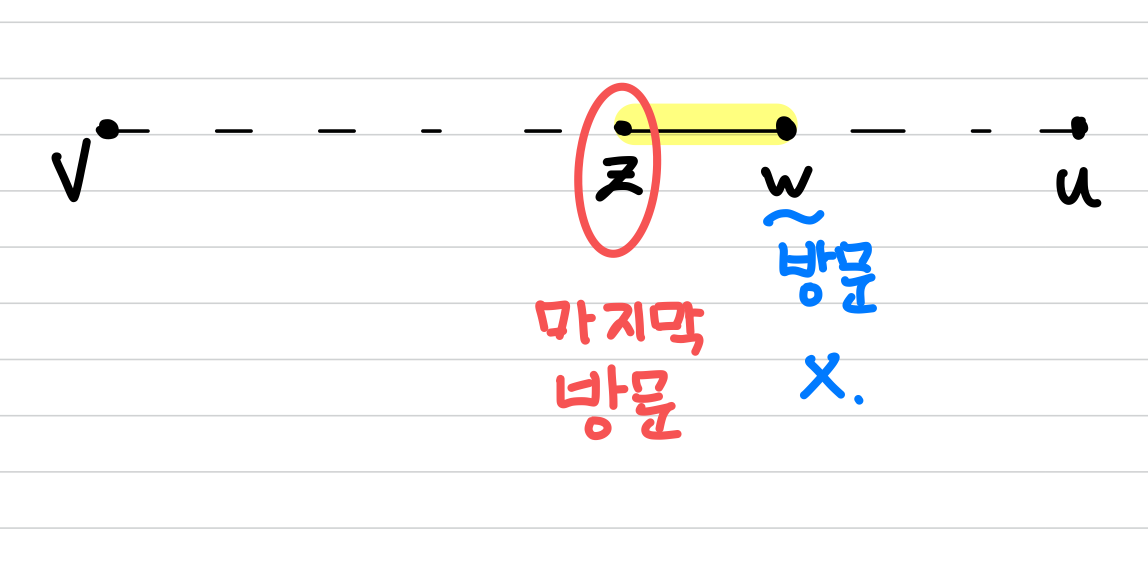
이때 해당 알고리즘을 보면 다음 부분이 있습니다.

즉 두 점 사이를 잇는 간선이 존재하면 반드시 방문 처리를 합니다.(이는 가정이 아닌 '사실'입니다.)
그러나 $(z, w) \in E$ 임에도 불구하고, 방문하지 않으니 이는 $z$ 와 인접(adjacent)한 모든 정점을 방문한다는 사실에 모순됩니다.
따라서 위 알고리즘을 올바르게 동작합니다.
🖥 코드로 구현
다음 그래프를 구현해 보겠습니다.
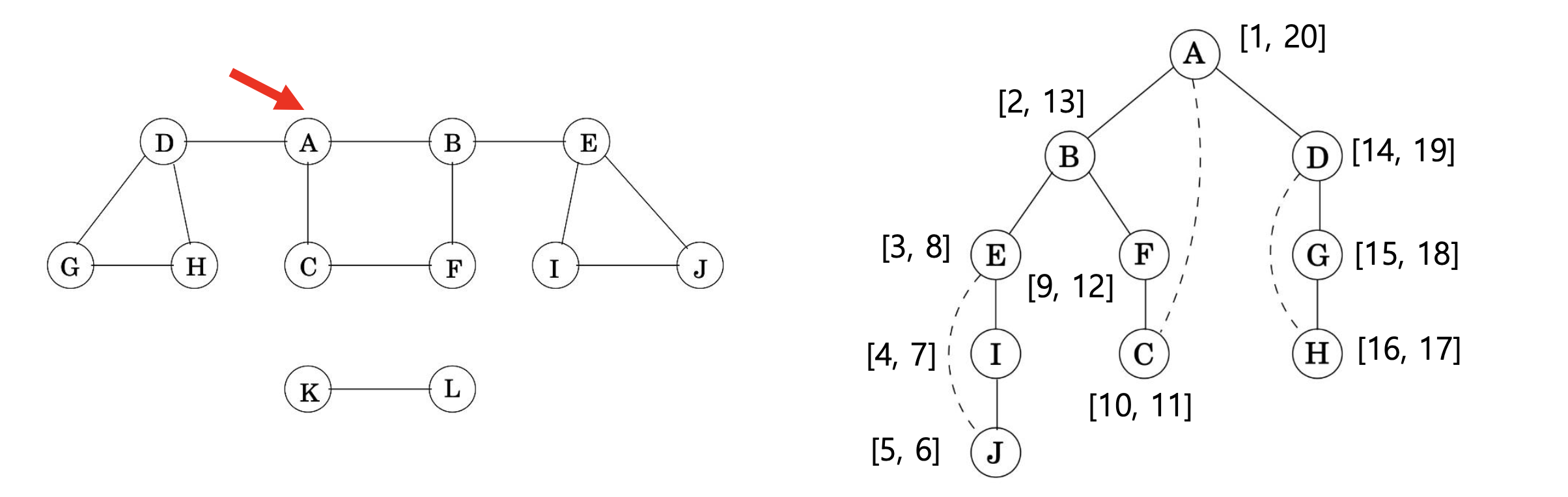
/**
* Created by ShinD on 2022/09/22.
*/
fun main() {
val graph = GraphMaker().make()
GraphExplorer().explore(graph, graph.vertexSet.elementAt(0))
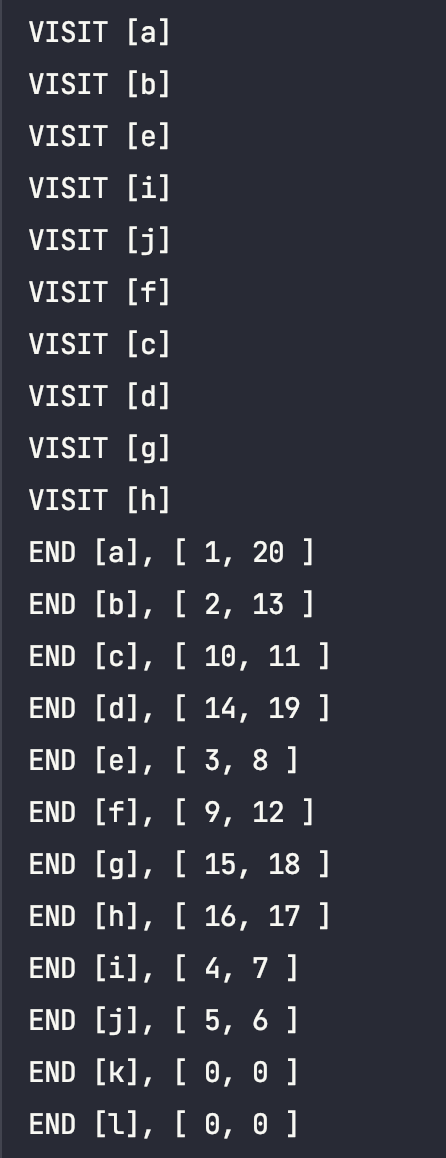
GraphMaker.vertexSet().forEach {
println("END [${it.value}], [ ${it.preOrder}, ${it.postOrder} ]")
}
}
class Graph(
val vertexSet: Set<Vertex>,
val graph: List<List<Vertex>>,
)
class GraphMaker {
companion object {
val a = Vertex('a')
val b = Vertex('b')
val c = Vertex('c')
val d = Vertex('d')
val e = Vertex('e')
val f = Vertex('f')
val g = Vertex('g')
val h = Vertex('h')
val i = Vertex('i')
val j = Vertex('j')
val k = Vertex('k')
val l = Vertex('l')
fun vertexSet(): Set<Vertex> {
return setOf(
a, b, c, d, e, f, g, h, i, j, k, l
)
}
}
fun make(): Graph {
return Graph(
vertexSet = vertexSet(),
graph = listOf(
listOf(b, c, d), // a
listOf(a, e, f), // b
listOf(a, f), // c
listOf(a, g, h), // d
listOf(b, i, j), // e
listOf(b, c), // f
listOf(d, h), // g
listOf(d, g), // h
listOf(e, j), // i
listOf(e, i), // j
listOf(l), // k
listOf(k), // l
)
)
}
}
class Vertex(
val value: Char,
var preOrder: Int = 0,
var postOrder: Int = 0,
var isVisited: Boolean = false,
) {
override fun equals(other: Any?): Boolean {
if (this === other) return true
if (other !is Vertex) return false
if (preOrder != other.preOrder) return false
if (postOrder != other.postOrder) return false
if (value != other.value) return false
return true
}
override fun hashCode(): Int {
var result = preOrder
result = 31 * result + postOrder
result = 31 * result + value.hashCode()
return result
}
}
class GraphExplorer {
// 시작 전 1로 초기화
private var counter = 1
private fun visited(vertex: Vertex) {
vertex.isVisited = true
println("VISIT [${vertex.value}]")
}
private fun preVisit(vertex: Vertex) {
vertex.preOrder = counter
counter++
}
private fun postVisit(vertex: Vertex) {
vertex.postOrder = counter
counter++
}
fun explore(
graph: Graph,
root: Vertex,
) {
val idx = root.value - 'a'
// 방문 처리
visited(root);
// preVisit
preVisit(root);
// 루트 vertex와 adjacent 한 모든 vertex 탐색
graph.graph[idx].forEach { vertex ->
/// 아직 방문하지 않았다면 explore
if (!vertex.isVisited) explore(graph, vertex)
}
// postVisit
postVisit(root);
}
}
🧐 previsit, postvisit는 뭐예요??
수행하는 작업은 매우 간단합니다.
우선 해당 procedure에 등장하는 정점들은 모두 preorder number와 postorder number 값을 가지고 있습니다.
해당 Procedure 시작 전, 어떠한 정수(여기서는 counter)를 1로 초기화 한 후
previsit(v)를 할 때마다 preorder number,
postvisit(v)를 할 때마다 postorder number 의 값을 counter의 값으로 설정한 후, counter를 1 증가시킵니다.
🧐 어따 쓰는데요???
좀 이따 나오니까 그때 알아보고, 지금은 다시 procedure로 돌아가 새로운 개념들을 알아보도록 하겠습니다.
앞선 explore 연산의 수행 과정을 (ordered) tree로 나타낼 수 있으며, 이를 DFS tree라고 부릅니다.
DFS tree의 root node는 처음 explore를 시작하는 정점이 됩니다.
explore ($G,$ $v$) 수행 도중, explore($G,$ $u$)를 재귀호출할 경우, $u$ 의 부모 노드(parent node)는 $v$ 가 됩니다.
그림으로 살펴보겠습니다.
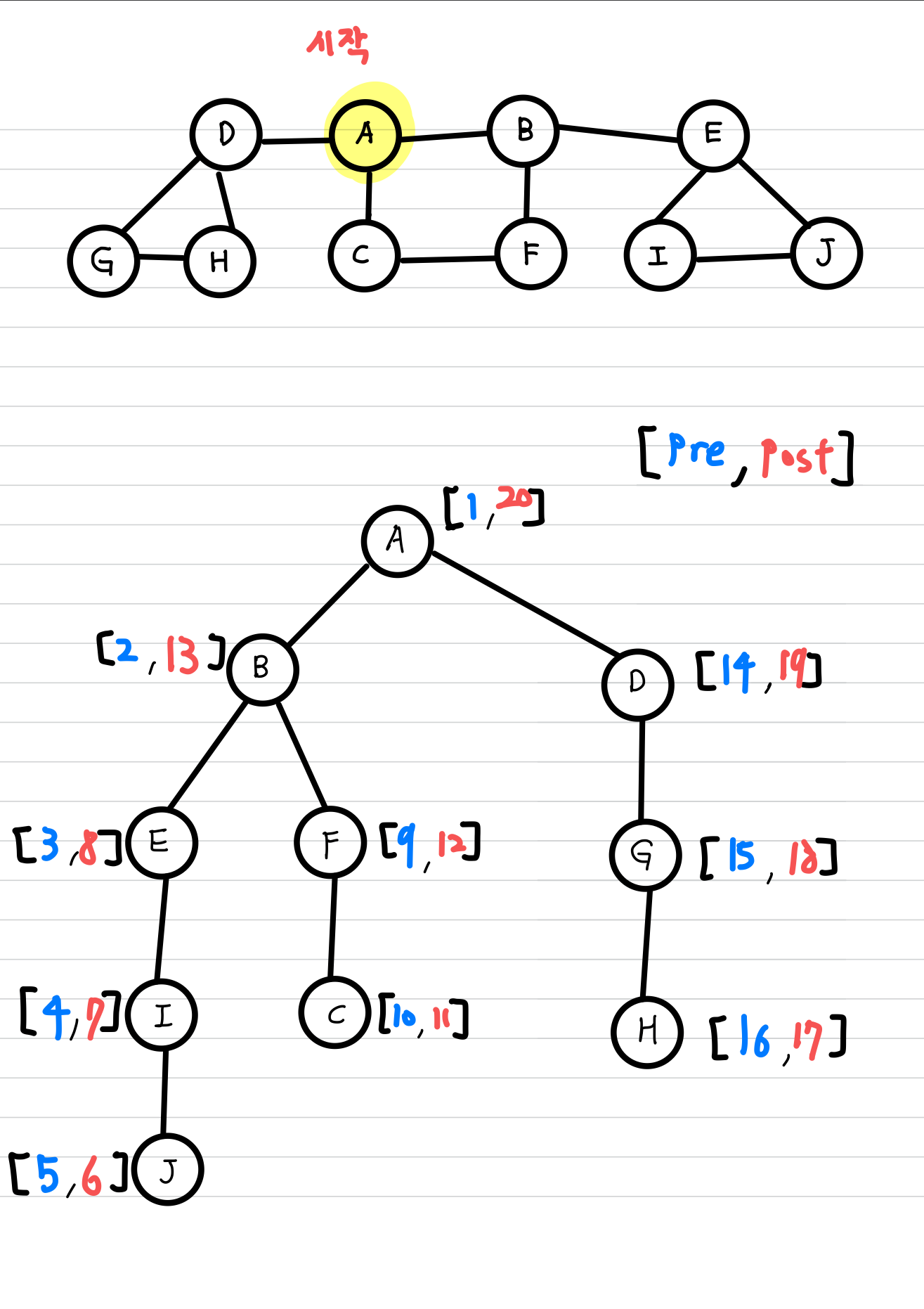
트리를 살펴보면 문제가 없는 것 같지만, 기존 그래프에 포함된 간선들이 포함되지 않은 것을 찾을 수 있습니다.
예를 들면 A와 C를 이어주는 간선처럼 말입니다.
그래프 G의 간선들 중 DFS tree에 있는 간선을 tree edge라 하며,
DFS tree에 없는 간선을 back edge라고 합니다.
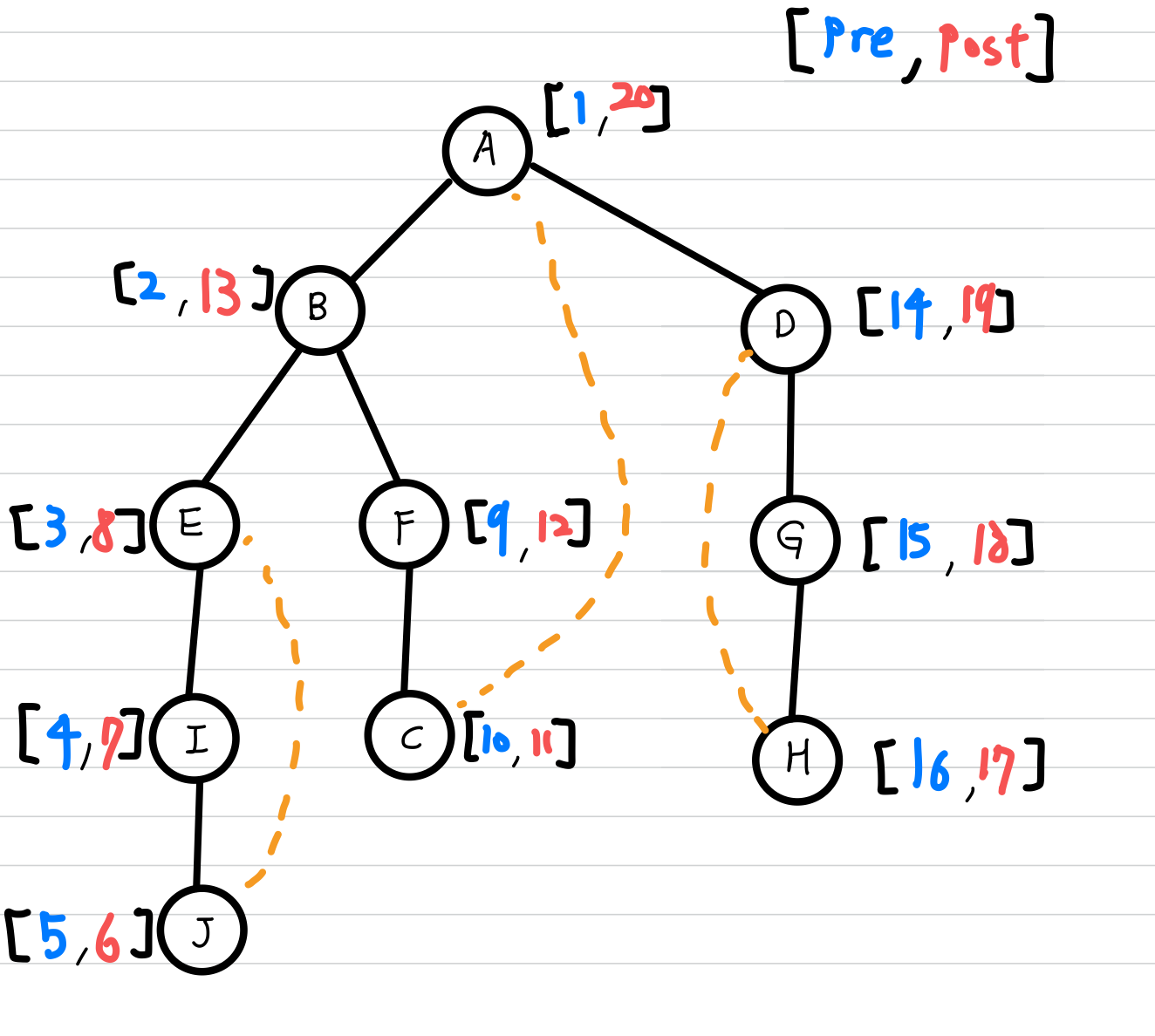
일반적으로 back edge는 점선으로 나타내며, 위의 예시에서는 다음과 같습니다.
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 (3) - 연결 요소(Connected Components)와 단절점(Articulation Point) (0) | 2022.09.24 |
|---|---|
| [알고리즘] 그래프 (2) - DFS (0) | 2022.09.24 |
| [알고리즘] Selection 알고리즘 (0) | 2022.09.19 |
| [알고리즘] 분할 정복(Divide and Conquer)과 Master Theorem (0) | 2022.09.11 |
| [알고리즘] 곱하기(Multiplication) 알고리즘 ($O(n^2)$) (0) | 2022.09.11 |
🧐 그래프 (Graph)
그래프는 정점(vertex)들과 간선(edge)들로 이루어진 구조로써, 기호로는 다음과 같이 표현합니다.
$$G = (V(G), E(G))$$
$V$ 는 정점을, $E$ 는 간선을 의미합니다.
🧐 Simple Graph
Self loop 또는 Multiple Edge를 가지지 않는 그래프를 Simple Graph라고 합니다.
그림으로는 아래와 같습니다.

앞으로 등장하는 모든 그래프는, 특별한 설명이 없는 이상 Simple Graph라고 가정하겠습니다.
🧐 Directed Graph와 Undirected Graph
그래프에 속한 $E$ (간선)의 각 원소들이 ordered pair 즉 방향성이 있는 경우, 해당 그래프를 방향 그래프(Directed Graph)라고 합니다.
반대로 $E$ (간선)의 각 원소들이 unordered pair 즉 방향성이 없는 경우, 해당 그래프를 무방향 그래프(Undirected Graph)라고 합니다.

🧐 Adjacent
두 정점 $v,\; u$ 에 대하여 $(v, u)\in E$ 일 때, 즉 두 정점을 잇는 간선이 존재하는 경우,
$v$ 는 $u$ 와 adjacent(인접하다)라고 표현합니다.
Undirected Graph의 경우 $v$ 와 $u$ 가 adjacent 하다면, $v$ 와 $u$ 역시 adjacent 입니다.
🧐 Degree (차수)
어떠한 정점 $v$ 에 대한 차수(degree)는 그래프 $G$ 에서 $v$ 와 adjacent한 정점의 수를 의미합니다.
Directed Graph의 경우 in-degree와 out-degree를 따로 정의하여 사용하지만, 고려하지 않고 넘어가도록 하겠습니다.
🧐 Subgraph (부분 그래프)
그래프 $G = (V(G), E(G))$ 에서 그래프 $G$ 의 subgraph $G' = (V(G'), E(G'))$ 는 다음과 같은 조건을 만족합니다.
1. $V(G') \subseteq V(G)$ : 서브그래프 $G'$ 에 속하는 정점들의 집합은, 그래프 $G$ 의 정점들의 부분집합이어야 합니다.
2. $E(G') \subseteq E(G) $ : 서브그래프 $G'$ 에 속하는 간선들의 집합은, 그래프 $G$ 의 간선들의 부분집합이어야 합니다.
3. $E(G')$ 에 속하는 모든 간선들은 $V(G')$ 의 정점들만을 사용해야 합니다.
예시는 아래와 같습니다.

🧐 Walk(보행), Trail, Path(경로), Circuit(회로 ), Cycle(순환)
(해당 부분의 정의들은 책마다 다르게 정의될 수 있으며, 저는 제가 참고하는 책을 기준으로 정리한 것입니다.)
✔️ Walk(보행)
그래프에 속한 두 정점을 골랐을 때, 두 정점이 어떻게든 연결되어 있다면 두 정점 사이에 보행이 존재한다고 표현합니다.
정의는 다음과 같습니다.
$v_1$ , $e_1$ , $v_2$ , $e_2$ , ..., $e_k$ , $v_k$ 로 이어지는,
정점 $v_1, \; v_2, \; ...$ 과 간선 $e_1, \; e_2\; ..$ 가 서로 교차되며 나타나는 sequence(혹은 alternating sequence)를 의미합니다.
정점 사이를 이동하기 위해서는 간선이 반드시 필요하므로, 어찌보면 당연한 정의일 수 있습니다.
보행(Walk)은 정점과 간선이 교차되야 한다는 것 외에는 제약조건이 존재하지 않습니다.
앞으로 나오는 개념들은 보행에 추가적인 제약조건이 걸린 개념들입니다.
✔️ Trail
제약조건: 같은 간선(Edge)이 두 번 이상 반복되면 안됩니다.
제약조건을 통한 Trail의 정의는 다음과 같습니다.
같은 간선(Edge)이 두 번 이상 반복되지 않는 Walk(보행)을 의미합니다.
✔️ Path(경로)
제약조건: 같은 정점(Vertex)이 두 번 이상 반복되면 안됩니다.
제약조건을 통한 Path의 정의는 다음과 같습니다.
같은 정점(Vertex)이 두 번 이상 반복되지 않는 Walk(보행)을 의미합니다.
Undirected Graph에서는 Path인 경우 Trail를 만족하지만, 그 역은 성립하지 않습니다.
(8자를 그린다고 생각해보세요)
🐛암기 Tip
트패는 애벌래
- 트(Trail) - 애(Edge)가 반복되지 않음
- 패(Path) - 벌(Vertex)가 반복되지 않음
✔️ Circuit(회로)
제약조건:
같은 간선(Edge)이 두 번 이상 반복되지 않으며,
시작 정점(Vertex)과 마지막 정점이 동일해야 합니다.
제약조건을 통한 Circuit(회로)의 정의는 다음과 같습니다.
같은 간선(Edge)이 두 번 이상 반복되지 않고, 시작 정점(Vertex)과 마지막 정점이 동일한 Walk(보행)를 의미합니다.
이는 다음과도 같습니다.
시작 정점(Vertex)과 마지막 정점이 동일한 Trail을 의미합니다.
✔️ Cycle(순환)
제약조건:
같은 간선(Edge)이 두 번 이상 반복되지 않으며,
시작 정점(Vertex)과 마지막 정점이 동일해야 하고,
이 두 정점을 제외한 나머지 정점들은 두 번 이상 반복되지 않아야 합니다.
제약조건을 통한 Cycle(순환)의 정의는 다음과 같습니다.
같은 간선(Edge)이 두 번 이상 반복되지 않고,
시작 정점(Vertex)과 마지막 정점이 동일하며,
이외 나머지 정점들은 두 번 이상 반복되지 않는 Walk(보행)를 의미합니다.
이는 다음과도 같습니다.
시작 정점(Vertex)과 마지막 정점이 동일하며, 이외 나머지 정점은 반복되지 않는 Trail을 의미합니다.
시작 정점(Vertex)과 마지막 정점을 제외하고 같은 정점이 두 번 이상 반복되지 않는 Circuit(회로)을 의미합니다.
예시

🧐 Connected Graph
(Directed Graph의 경우는 뒤에서 따로 정의하도록 하겠습니다.)
Undirected Graph $G = (V, E)$ 에서 다음 조건을 만족하는 경우 그래프 $G$ 를 Connected Graph라 표현합니다.
임의의 서로 다른 두 정점(vertex) $v, w \in V$ 에 대하여, $v$ 에서 $w$ 로의 path가 존재합니다.
이 경우 G는 Connected 하다고도 표현합니다.
임의의 두 정점을 고르는 것이므로, 그래프에 존재하는 모든 점에 대해서 서로간의 path가 존재해야 하는 것입니다.
Connected 하지 않은 그래프는 disconnected(비연결)라고 합니다.
🧐 그래프와 시간복잡도
그래프를 코드 상으로 표현하는 방법에는 배열을 사용하는 방법과 리스트를 사용하는 방법이 있습니다.
리스트는 조금 헷갈릴 수도 있으므로, 이해를 돕기 위해 사진을 추가하겠습니다.

그래프에서 행해질 수 있는 여러 연산들에 대하여, 두 방법간의 시간 복잡도 차이를 알아보도록 하겠습니다.
| 배열에 저장 | 리스트에 저장 | |
| 공간(Space) | $O(n^{2})$ | $O(n + m)$ |
| 정점 $u$ 와 $v$ 가 인접(adjacent)한지 확인 | $O(1)$ | $O(deg(u))$ |
| 정점 $u$ 와 인접(adjacent)한 모든 정점 확인 | $O(n)$ | $O(deg(u))$ |
| 정점 $u$ 의 차수 구하기 | $O(n)$ | $O(deg(u))$ |
이제부터 나오는 알고리즘에 대해서는, 모두 list에 저장되어 있다고 가정하도록 하겠습니다.
🧐 Reachability (접근 가능성)
Undirected graph $G$ 의 두 정점(vertex) $u$, $v$ 에 대하여,
정점 $u$ 에서 $v$ 로의 path가 있으면,
$v$ 는 $u$ 로부터 reachable(접근 가능한)이라고 합니다.

🧐 Reachability 알고리즘
어떠한 정점 $v$ 에서 reachable한 모든 정점들을 찾는 알고리즘은 다음과 같습니다.

해당 알고리즘이 올바르게 동작함은 다음과 같이 증명할 수 있습니다.
👉 증명
증명하고자 하는 정리(Theorem)는 다음과 같습니다.
explore($G, \;v$)는 올바르게 동작한다.
증명은 귀류법(Proof by Contradiction)을 통해 진행됩니다.
'explore($G, \; v$) 가 v에서 reachable한 어떤 정점 $u$ 를 방문하지 않는다'고 가정하겠습니다.
그리고 $v$ 와 $u$ 사이의 Path에 존재하는 정점들 중 마지막으로 방문한 정점을 $z$ 라 하겠습니다.
그리고 $z$ 이후에 바로 나오는 정점을 $w$ 라 가정하겠습니다.
(이해를 돕기 위한 그림으로는 다음과 같습니다.)

이때 해당 알고리즘을 보면 다음 부분이 있습니다.

즉 두 점 사이를 잇는 간선이 존재하면 반드시 방문 처리를 합니다.(이는 가정이 아닌 '사실'입니다.)
그러나 $(z, w) \in E$ 임에도 불구하고, 방문하지 않으니 이는 $z$ 와 인접(adjacent)한 모든 정점을 방문한다는 사실에 모순됩니다.
따라서 위 알고리즘을 올바르게 동작합니다.
🖥 코드로 구현
다음 그래프를 구현해 보겠습니다.

/**
* Created by ShinD on 2022/09/22.
*/
fun main() {
val graph = GraphMaker().make()
GraphExplorer().explore(graph, graph.vertexSet.elementAt(0))
GraphMaker.vertexSet().forEach {
println("END [${it.value}], [ ${it.preOrder}, ${it.postOrder} ]")
}
}
class Graph(
val vertexSet: Set<Vertex>,
val graph: List<List<Vertex>>,
)
class GraphMaker {
companion object {
val a = Vertex('a')
val b = Vertex('b')
val c = Vertex('c')
val d = Vertex('d')
val e = Vertex('e')
val f = Vertex('f')
val g = Vertex('g')
val h = Vertex('h')
val i = Vertex('i')
val j = Vertex('j')
val k = Vertex('k')
val l = Vertex('l')
fun vertexSet(): Set<Vertex> {
return setOf(
a, b, c, d, e, f, g, h, i, j, k, l
)
}
}
fun make(): Graph {
return Graph(
vertexSet = vertexSet(),
graph = listOf(
listOf(b, c, d), // a
listOf(a, e, f), // b
listOf(a, f), // c
listOf(a, g, h), // d
listOf(b, i, j), // e
listOf(b, c), // f
listOf(d, h), // g
listOf(d, g), // h
listOf(e, j), // i
listOf(e, i), // j
listOf(l), // k
listOf(k), // l
)
)
}
}
class Vertex(
val value: Char,
var preOrder: Int = 0,
var postOrder: Int = 0,
var isVisited: Boolean = false,
) {
override fun equals(other: Any?): Boolean {
if (this === other) return true
if (other !is Vertex) return false
if (preOrder != other.preOrder) return false
if (postOrder != other.postOrder) return false
if (value != other.value) return false
return true
}
override fun hashCode(): Int {
var result = preOrder
result = 31 * result + postOrder
result = 31 * result + value.hashCode()
return result
}
}
class GraphExplorer {
// 시작 전 1로 초기화
private var counter = 1
private fun visited(vertex: Vertex) {
vertex.isVisited = true
println("VISIT [${vertex.value}]")
}
private fun preVisit(vertex: Vertex) {
vertex.preOrder = counter
counter++
}
private fun postVisit(vertex: Vertex) {
vertex.postOrder = counter
counter++
}
fun explore(
graph: Graph,
root: Vertex,
) {
val idx = root.value - 'a'
// 방문 처리
visited(root);
// preVisit
preVisit(root);
// 루트 vertex와 adjacent 한 모든 vertex 탐색
graph.graph[idx].forEach { vertex ->
/// 아직 방문하지 않았다면 explore
if (!vertex.isVisited) explore(graph, vertex)
}
// postVisit
postVisit(root);
}
}
🧐 previsit, postvisit는 뭐예요??
수행하는 작업은 매우 간단합니다.
우선 해당 procedure에 등장하는 정점들은 모두 preorder number와 postorder number 값을 가지고 있습니다.
해당 Procedure 시작 전, 어떠한 정수(여기서는 counter)를 1로 초기화 한 후
previsit(v)를 할 때마다 preorder number,
postvisit(v)를 할 때마다 postorder number 의 값을 counter의 값으로 설정한 후, counter를 1 증가시킵니다.
🧐 어따 쓰는데요???
좀 이따 나오니까 그때 알아보고, 지금은 다시 procedure로 돌아가 새로운 개념들을 알아보도록 하겠습니다.
앞선 explore 연산의 수행 과정을 (ordered) tree로 나타낼 수 있으며, 이를 DFS tree라고 부릅니다.
DFS tree의 root node는 처음 explore를 시작하는 정점이 됩니다.
explore ($G,$ $v$) 수행 도중, explore($G,$ $u$)를 재귀호출할 경우, $u$ 의 부모 노드(parent node)는 $v$ 가 됩니다.
그림으로 살펴보겠습니다.

트리를 살펴보면 문제가 없는 것 같지만, 기존 그래프에 포함된 간선들이 포함되지 않은 것을 찾을 수 있습니다.
예를 들면 A와 C를 이어주는 간선처럼 말입니다.
그래프 G의 간선들 중 DFS tree에 있는 간선을 tree edge라 하며,
DFS tree에 없는 간선을 back edge라고 합니다.
일반적으로 back edge는 점선으로 나타내며, 위의 예시에서는 다음과 같습니다.

'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 (3) - 연결 요소(Connected Components)와 단절점(Articulation Point) (0) | 2022.09.24 |
|---|---|
| [알고리즘] 그래프 (2) - DFS (0) | 2022.09.24 |
| [알고리즘] Selection 알고리즘 (0) | 2022.09.19 |
| [알고리즘] 분할 정복(Divide and Conquer)과 Master Theorem (0) | 2022.09.11 |
| [알고리즘] 곱하기(Multiplication) 알고리즘 ($O(n^2)$) (0) | 2022.09.11 |