728x90
🧐 방향성이 있는 그래프에서의 DFS
방향성이 있는 그래프(Directed Graph) 에서도 Undirected Graph와 똑같은 방법으로 DFS가 가능합니다.
그러나 Directed Graph에서는 간선에 방향성이 있으므로,
undirected graph와 달리 DFS Tree에서 Tree Edge가 아닌 부분들을 더 세분화 할 수 있습니다.
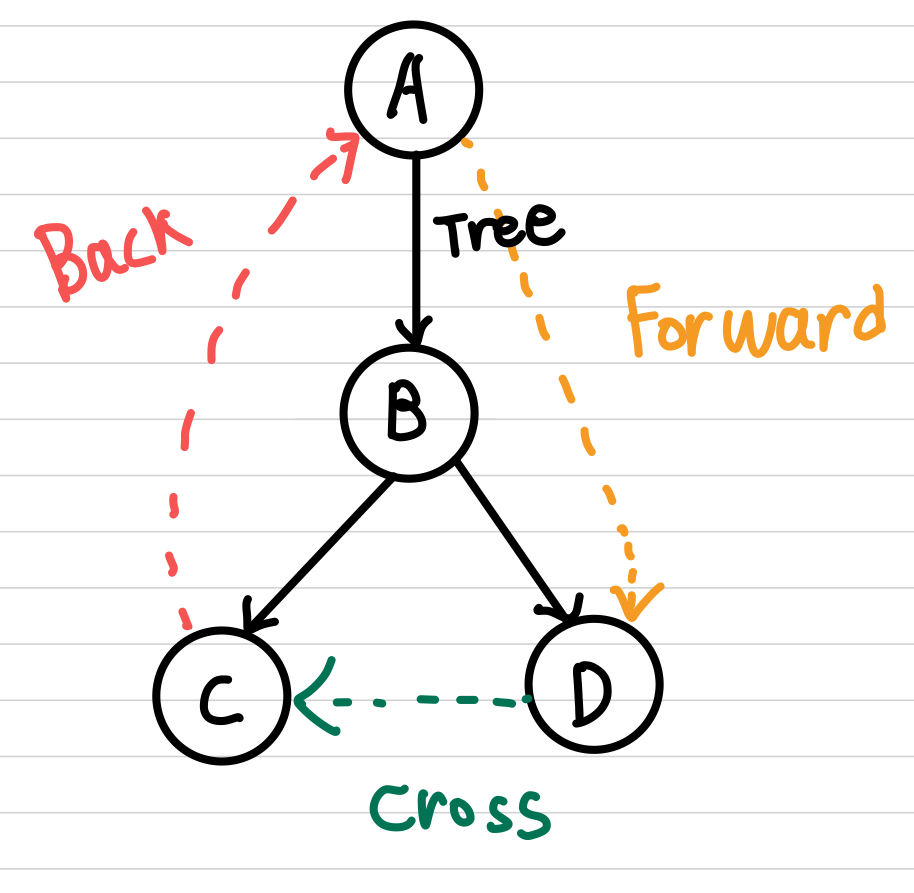
Directed Graph에서 DFS Tree에 등장하는 Edge는 다음과 같습니다.
Tree Edge : Undirected Graph와 동일합니다. DFS Tree 상에 표시되는 간선을 의미합니다.
Back Edge $($ $u$, $v$ $)$: $u$ 는 $v$ 의 descendant
Forward Edge $($ $u$, $v$ $)$ : $u$ 는 $v$ 의 ancestor
Cross Edge : 나머지 Edge를 의미합니다
🧐 방향성이 있는 그래프에서 PreOrder와 PostOrder의 특징
Directed Graph의 간선 $($ $u$, $v$ $)$ 에 대하여, $pre(v)$, $post(v)$, $pre(u)$, $post(u)$는 다음 세가지 관계만을 가집니다.
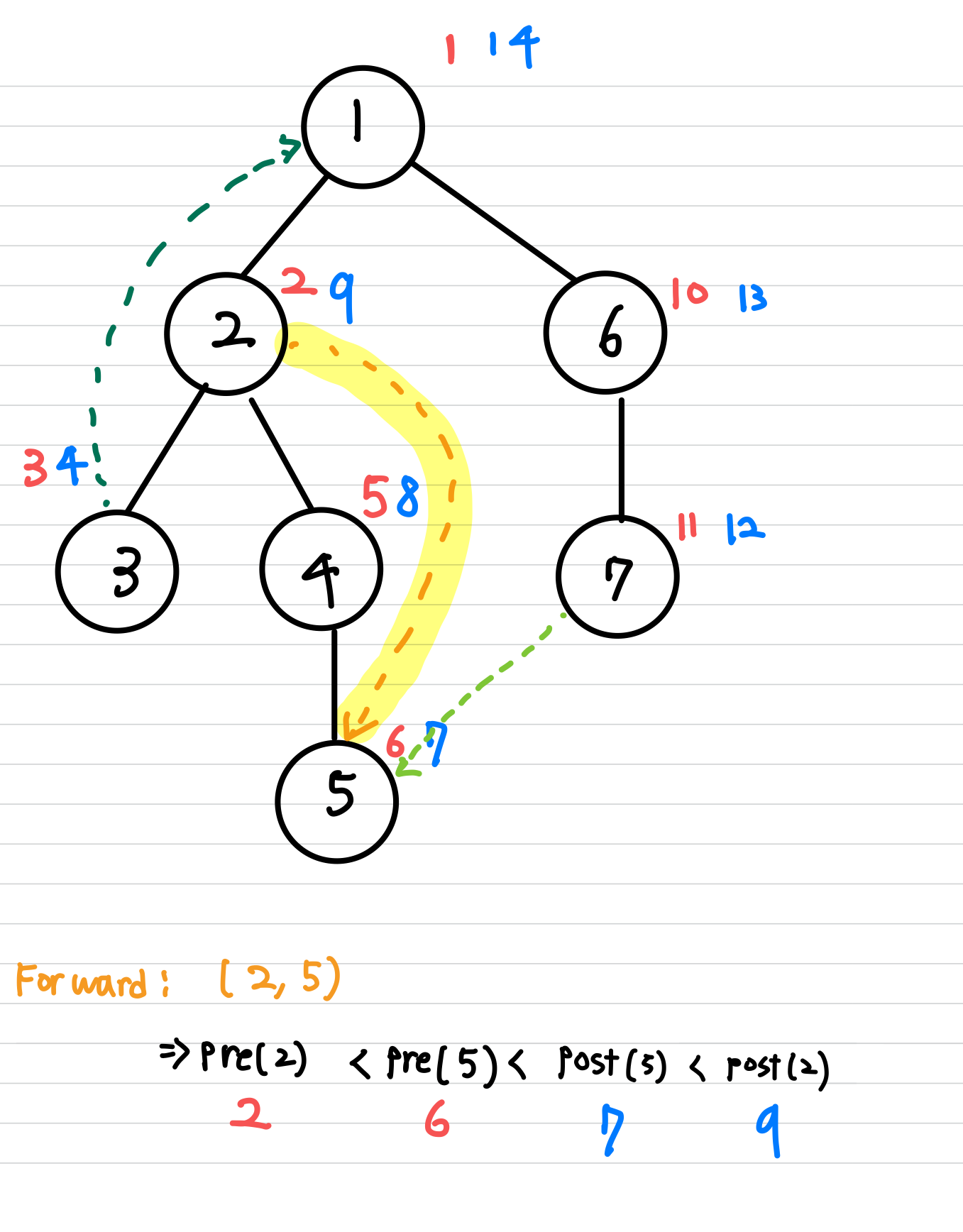
$($ $u$, $v$ $)$ 가 tree edge 혹은 forward edge인 경우
$pre(u)$ $<$ $pre(v)$ $<$ $post(v)$ $<$ $post(u)$
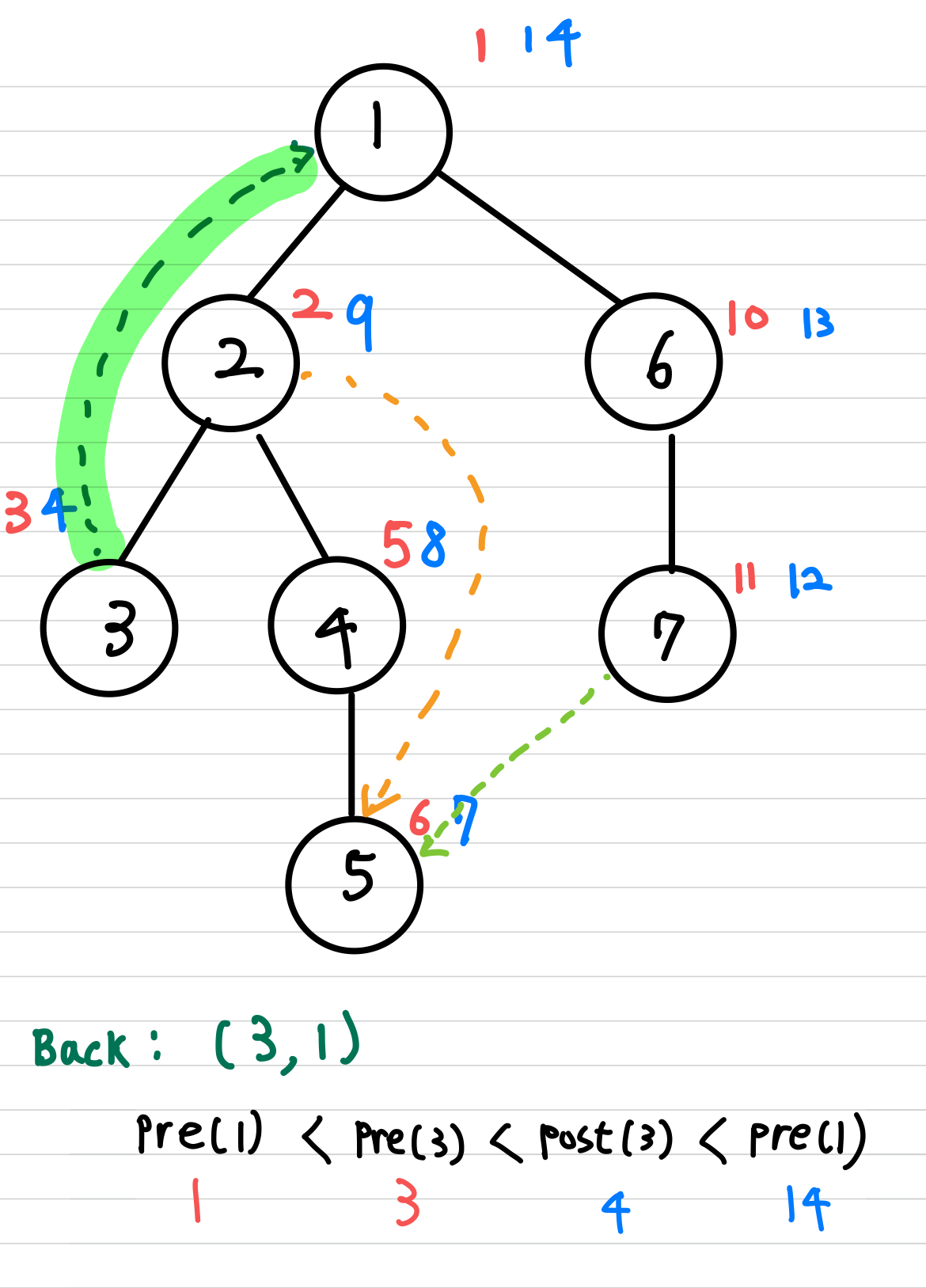
$($ $u$, $v$ $)$ 가 back edge인 경우
$pre(v)$ $<$ $pre(u)$ $<$ $post(u)$ $<$ $post(v)$
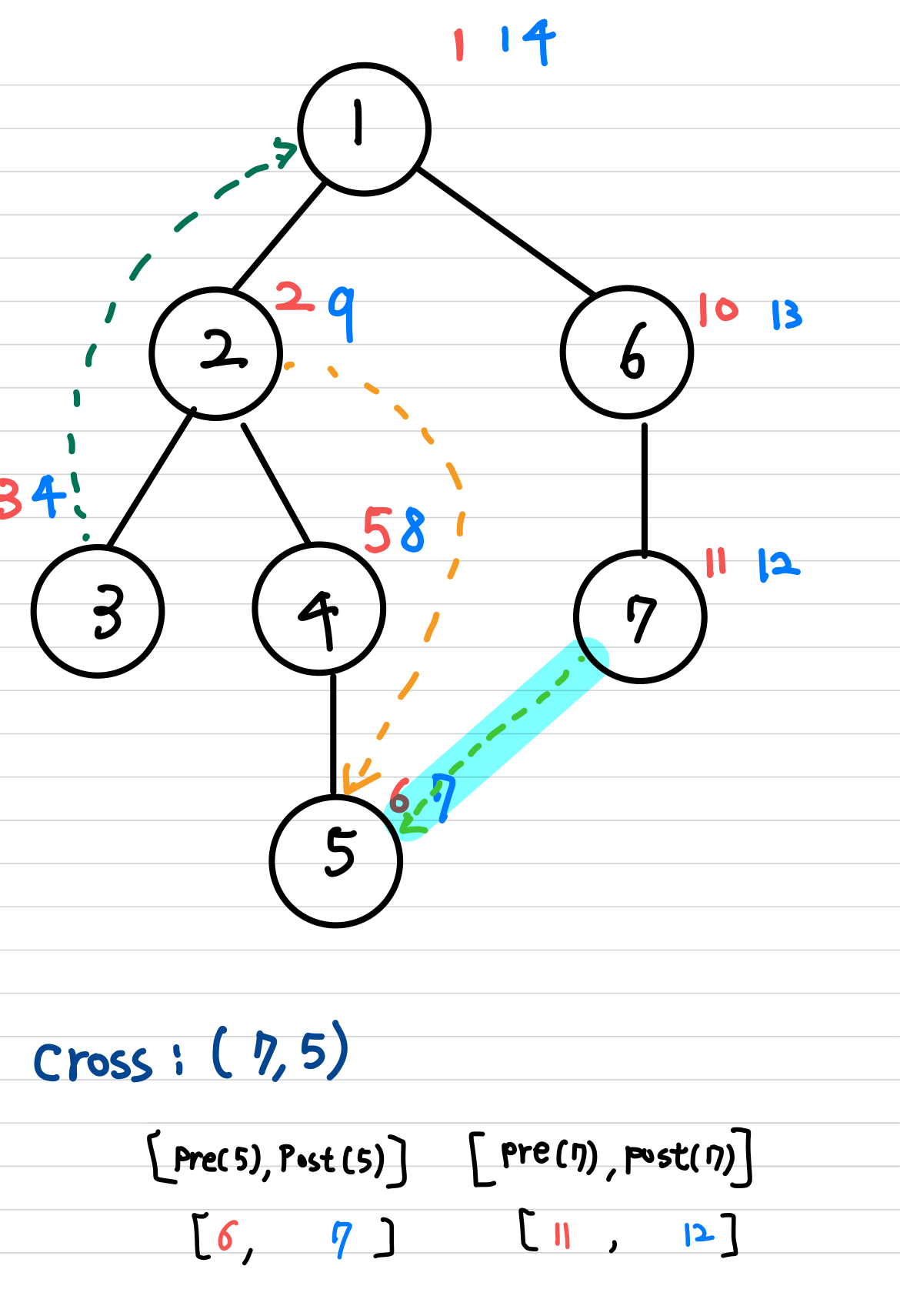
$($ $u$,$v$ $)$가 cross edge인 경우
$[pre(u),post(u)]$ $[pre(v), post(v)]$ 가 disjoint 입니다.
728x90
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 (7) - 강한 연결 요소 (Strongly Connected Components) (1) | 2022.09.25 |
|---|---|
| [알고리즘] 그래프 (6) - 위상 정렬(Topological Sort) (1) | 2022.09.24 |
| [알고리즘] 그래프 (4) - 이중 연결 요소 (Biconnected Components) (0) | 2022.09.24 |
| [알고리즘] 그래프 (3) - 연결 요소(Connected Components)와 단절점(Articulation Point) (0) | 2022.09.24 |
| [알고리즘] 그래프 (2) - DFS (0) | 2022.09.24 |