🧐 Biconnected Components
그래프 $G$ 가 biconnected 하다는 것은 다음을 의미합니다.
$G$ 는 connected graph 이며, articulation point를 가지고 있지 않다.
biconnected를 통한 biconnected component의 정의는 다음과 같습니다.
Biconnected component $G’$ of $G$ : $G$ 의 maximal biconnected subgraph
즉 $G$ 의 biconnected component로 $G$ 의 간선들을 partitioning 할 수 있으며,
서로 다른 biconnected component는 최대 한개의 정점(articulation vertex)를 공유합니다.

따라서 위의 그림처럼 Articulation Point를 통해 그래프 내에 존재하는 Biconnected Components를 찾아낼 수 있습니다.
⭐️ Key Property
같은 BCC에 속해있는 edge $e$ 와 $e'$ 이 있을 때,
$e = e'$ 이거나 $e$ 와 $e'$ 을 모두 포함하는 cycle이 같은 component 안에 속해있습니다.
증명은 다음과 같습니다.
같은 BCC 안에 존재하는 edge $e$ 와 $e'$ 이 있을 때,
$e \neq e'$ 이며 $e$ 와 $e'$ 을 모두 포함하는 cycle이 같은 bcc 안에 없다고 가정하겠습니다.
$e$ 와 $e'$ 를 모두 포한하는 cycle에 속하면서 이들과 같은 bcc에 속하지 않는 정점을 $u$ 라고 하면,
$e$ 와 $e' $이 속한 BCC의 임의의 한 정점으로부터 $u$ 까지의 path 가 무조건 존재합니다.
(존재하지 않으면 cycle이 성립할 수 없기 때문입니다.)
또한 $u$ 는 $e$, $e'$ 과 같은 cycle에 속하기 때문에 $e$, $e'$ 가 속한 BCC의 임의의 한 정점을 제거하더라도 여전히 $u$로의 path가 존재합니다.
또한 가정에 의하여 기존 $e$ 와 $e' $ 를 포함하는 BCC는 $u$ 를 포함하지 않은 상태로 BCC 였기 때문에 $u$ 는 Articulation Point가 아닙니다.
따라서 기존 BCC에 $u$ 를 추가하더라도 여전히 BCC이므로, maximal 조건에 위배됩니다.
따라서 가정에 모순이 존재하므로, 증명이 완료됩니다.
🧐 Biconnected Conponent 찾아내는 알고리즘
우선 해당 알고리즘의 대상이 되는 그래프 $G$ 는 Connencted graph입니다.
Biconnected Component는 Articulation Point를 통해 찾아낼 수 있습니다.
Biconnected Component를 구하기 위해 다음 두가지의 문제를 해결해야 합니다.
첫번째 문제: 그래프 $G$ 의 모든 Articulation point 찾기
두번째 문제: 첫번째 문제를 이용해서 $G$ 의 Biconnected Component 찾기
이제 이 두 과정을 살펴보도록 하겠습니다.
✔️ 첫번째 문제 : 그래프 $G$ 의 모든 Articulation Point 찾기
이전 글에서 살펴보았습니다.
✔️ 두번째 문제 : Articulation Point 를 이용하여 Biconnected Component 찾기
이곳에서도 Graph는 Undirected Connected Graph라 가정합니다.
Biconnected Component는 edge를 Partitioning 합니다.
따라서 Biconnected Component를 하나 return 할 때마다, 해당 Component에 속해있는 edge들을 return하는 방식으로 구할 수 있습니다.
해당 알고리즘은 Stack을 이용하여 구현하면 간편합니다.
따라서 Stack을 사용한다는 조건 하에 해당 알고리즘의 과정을 설명하도록 하겠습니다.
정점 $v$ 를 explore 하면서 간선$($ $v$, $u$ $)$ 를 확인할 때마다 해당 간선을 Stack에 push 합니다.
만약 $v$ 를 explore 하면서, $v$ 의 자식 노드 $u$ 에 의하여,
$v$ 가 articulation point임이 밝혀지거나( = $low(u)$ $\geq$ $pre(v)$ ),
root node $v$ 의 한 child 대한 explore 가 종료된다면
간선$($ $u$ , $v$ $)$ 가 나올 때까지, stack 상의 모든 간선들을 pop 하며,
이것들이 하나의 Biconnected Component가 됩니다.
Articulation Point를 찾을 때와는 달리 root node인 경우를 따로 처리할 필요가 없습니다.
수도 코드

구현
마찬가지로 다음 그래프에 대한 구현입니다.
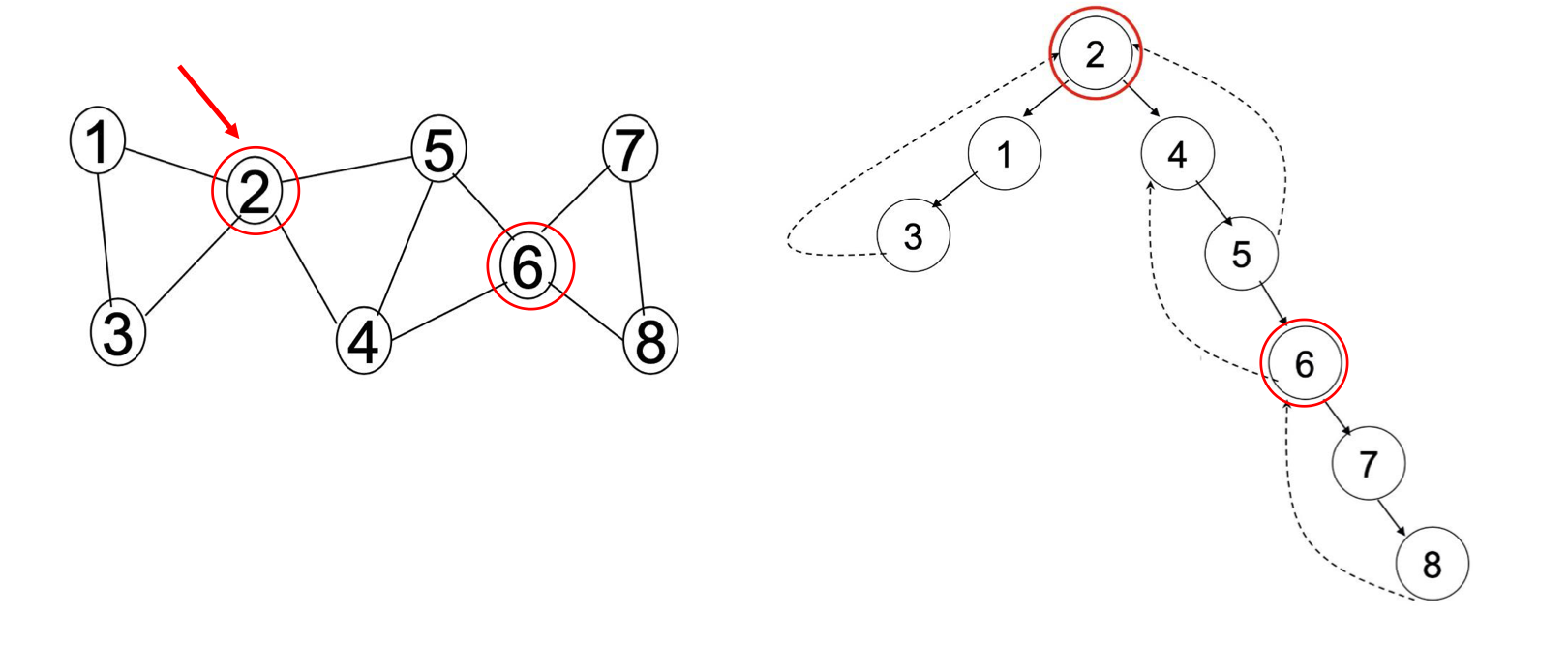
/**
* Created by ShinD on 2022/09/22.
*/
fun main() {
val graph = GraphMaker().make()
val biConnectedComponents = mutableListOf<List<Edge>>()
GraphExplorer().findBiConnectedComponent(
graph = graph,
current = GraphMaker.b,
stack = ArrayDeque(),
biConnectedComponents = biConnectedComponents,
)
GraphMaker.vertexSet().forEach {
println("END [${it.value}], [ ${it.preOrder}, ${it.postOrder} ], LOW = [${it.low}], IS_CUT_POINT = [${it.isCutPoint}]")
}
println()
biConnectedComponents.forEach { biConnectedComponent ->
println("BiConnected Component")
biConnectedComponent.forEach {
println("${it.startVertex.value}, ${it.endVertex.value}")
}
println()
println()
}
}
class Graph(
val vertexSet: Set<Vertex>,
val graph: List<List<Vertex>>,
)
class GraphMaker {
companion object {
val a = Vertex('1')
val b = Vertex('2')
val c = Vertex('3')
val d = Vertex('4')
val e = Vertex('5')
val f = Vertex('6')
val g = Vertex('7')
val h = Vertex('8')
fun vertexSet(): Set<Vertex> {
return setOf(
a, b, c, d, e, f, g, h,// i, j, k, l
)
}
}
fun make(): Graph {
return Graph(
vertexSet = vertexSet(),
graph = listOf(
listOf(b, c), // 1
listOf(a, c, d, e), // 2
listOf(a, b), // 3
listOf(b, e, f), // 4
listOf(b, d, f), // 5
listOf(d, e, g, h), // 6
listOf(f, h), // 7
listOf(f, g), // 8
)
)
}
}
class Vertex(
val value: Char,
var preOrder: Int = 0,
var postOrder: Int = 0,
var low: Int = 0,
var isVisited: Boolean = false,
var isCutPoint: Boolean = false,
)
class Edge(
val startVertex: Vertex,
val endVertex: Vertex,
){
override fun equals(other: Any?): Boolean {
if (this === other) return true
if (other !is Edge) return false
if (startVertex != other.startVertex) return false
if (endVertex != other.endVertex) return false
return true
}
override fun hashCode(): Int {
var result = startVertex.hashCode()
result = 31 * result + endVertex.hashCode()
return result
}
}
class GraphExplorer {
// 시작 전 1로 초기화
private var counter = 1
private fun visited(vertex: Vertex) {
vertex.isVisited = true
println("VISIT [${vertex.value}]")
}
private fun preVisit(vertex: Vertex) {
vertex.preOrder = counter
counter++
}
private fun postVisit(vertex: Vertex) {
vertex.postOrder = counter
counter++
}
fun findBiConnectedComponent(
graph: Graph, // Connected Graph
current: Vertex, // DFS 진행할 Vertex
parent: Vertex? = null,
stack: ArrayDeque<Edge>,
biConnectedComponents: MutableList<List<Edge>>
) {
val idx = current.value - '1'
// 방문 처리
visited(current)
// preVisit
preVisit(current)
// PreOrder 값으로 low 설정
current.low = current.preOrder
// 루트 vertex와 adjacent 한 모든 vertex 탐색
graph.graph[idx].forEach { vertex ->
// Back Edge인 경우
if (vertex.isVisited && vertex != parent ) {
current.low = Math.min(current.low, vertex.preOrder)
stack.add(Edge(current, vertex))
}
// 아직 방문하지 않았다면 explore
if (!vertex.isVisited) {
stack.add(Edge(current, vertex))
findBiConnectedComponent(graph, vertex, current, stack, biConnectedComponents)
current.low = Math.min(current.low, vertex.low)
if (vertex.low >= current.preOrder) { // 자식 노드(vertex) 에서 현재 노드(current)의 proper ancestor로 향하는 Back Edge가 없는 경우
current.isCutPoint = true; // current는 Articulation Point(Cut Point)
val biConnectedComponent = mutableListOf<Edge>()
while (!stack.isEmpty()) {
if (stack.last() == Edge(current, vertex)) { // 같은 Edge가 나오면 종료
biConnectedComponent.add(stack.removeLast())
break
}
biConnectedComponent.add(stack.removeLast())
}
biConnectedComponents.add(biConnectedComponent)
}
}
}
postVisit(current)
}
}
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 (6) - 위상 정렬(Topological Sort) (1) | 2022.09.24 |
|---|---|
| [알고리즘] 그래프 (5) - Directed Graph 에서의 DFS (0) | 2022.09.24 |
| [알고리즘] 그래프 (3) - 연결 요소(Connected Components)와 단절점(Articulation Point) (0) | 2022.09.24 |
| [알고리즘] 그래프 (2) - DFS (0) | 2022.09.24 |
| [알고리즘] 그래프 (1) - 그래프의 기본 용어 (0) | 2022.09.24 |