이번 글에서는 필요한 회로의 기능에 대한 설명 문장을 통한 조합논리회로의 설계를 다뤄보겠습니다.
첫 단계에서는 보통 회로에 기능에 대한 설명을 진리표 혹은 대수 표현식으로 변환하게 됩니다.
부울함수에 대한 진리표가 주어지면, 표준 논리곱의 합(최소항 전개)과 표준 논리합의 곱(최대항 전개)의 두 가지 함수의 표준 대수식을 얻을 수 있습니다.
이들을 간략화하여 AND와 OR 게이트로 이루어진 회로를 구성할 수 있게 됩니다.
🧐 문제 서술부의 부울식 변환
논리설계 문제는 종종 한 문장 혹은 여러 문장을 사용하여 서술되기도 합니다. 논리회로 설계의 첫 단계는 이들 문장을 부울식으로 변환하는 것입니다. 이렇게 하기 위해서는 각 문장을 구로 나누고 각 구를 부울변수와 연관시켜야 합니다.
어떤 한 구가 "참(true)" 혹은 "거짓(false)"의 진리값을 가진다면 이 구는 부울변수로 나타낼 수 있는데,
"신동훈은 집에서 공부를 한다", 혹은 "오늘은 월요일이다"와 같은 구는 참 혹은 거짓일 수 있습니다.
하지만 "공부를 해라"는 명령은 진리값을 가지지 않습니다. 문장이 여러 구로 되어있을 떄 각 구를 중괄호를 사용하여 구분할 수 있습니다. 다음 문장을 세 구로 되어 있습니다.
Mary watches TV if it is Monday night and she has finished her homework.
어떤 구에도 "if"와 "and"는 포함되지 않습니다.
이것들은 단지 구 사이의 연결을 나타낼 뿐입니다.
F = 1 if "Mary watches TV" is true; otherwise, F = 0
A = 1 if "it is Monday night" is true; otherwise, A = 0
B = 1 if "she has finished her homework" is true; otherwise, B = 0
A와 B 모두가 "참"일 때 F가 "참"이므로, 이 문장은 다음과 같이 나타낼 수 있습니다.
F = AB
🧐 진리표를 사용하는 조합논리설계
예시를 위해 2진수 N을 가정하도록 하겠습니다.
어떤 스위칭회로는 입력이 A, B, C 셋이고, 출력이 하나입니다.
A, B, C는 각각 2진수 N의 첫 번째, 두 번째, 세 번째 비트를 나타냅니다.
이 회로는 N이 011 이상이면 f =1 이고, 미만이라면 f = 0입니다.
이 회로를 대수식으로 표현하기 위해 진리표를 그려보도록 하겠습니다.
| A B C | f | f' |
| 0 0 0 | 0 | 1 |
| 0 0 1 | 0 | 1 |
| 0 1 0 | 0 | 1 |
| 0 1 1 | 1 | 0 |
| 1 0 0 | 1 | 0 |
| 1 0 1 | 1 | 0 |
| 1 1 0 | 1 | 0 |
| 1 1 1 | 1 | 0 |
이제 이 진리표를 보고 f = 1 인 경우에, A,B,C의 진리값 조합으로 진리표에서 f의 대수식을 구합니다.
A가 0의 값을 가지고, B와 C가 1의 값을 가질때 f = 1입니다. 따라서 이는 다음과 같이 표현됩니다.
$$A'BC$$
이와 같이 1이 되는 모든 항을 구해서 OR 연산을 취하도록 하겠습니다. (OR 연산을 취하는 이유는 1이 되는 항들 여러개가 있을 때, 단 하나의 항만 1이 되어도 그 값은 1이 나오기 때문입니다.)
$$f = A'BC + AB'C' + AB'C + ABC' + ABC$$
위 식은 A, B, C의 입력이 011, 100, 101, 110, 111 값들 중 어느 하나일 때 1이 됩니다.
다른 입력 조합일 때는 식의 5개항 모두가 0이 되기 때문에, f는 0의 값을 가지게 됩니다.
이제 위 식을 간략화 하도록 하겠습니다. 지금까지 배운 부울 대수 정리와 간략화 식을 적용하면 다음과 같이 바뀝니다.
$$ f = A + BC $$
함수를 1에 대하여 구하는 것이 아닌 0에 대하여 구할 수도 있습니다.
A + B + C 항은 A, B, C 모두가 0인 경우에만 0이 됩니다.
이런 식으로 0이 되는 항들을 보아 AND하면 다음과 같은 식이 만들어집니다.
$$f = (A + B + C)(A + B + C')(A + B' + C)$$
이제 위 식도 간략화 하도록 하겠습니다.
$$f = A + BC$$
🧐 최소항과 최대항 전개
🌱 최소항(minterm)
다음 식을 보도록 하겠습니다.
$$f = A'BC + AB'C' + AB'C + ABC' + ABC$$
위 항에서 각 항을 최소항(minterm)이라고 합니다. 일반적으로 n개의 변수의 최소항은 각 변수가 그대로 혹은 보수 형태로 단 한 번씩만 나타나는 n개 문자의 곱입니다.
최소항은 때때로 간단한 형태로 나타낼 수 있는데, A'B'C'는 m0, A'B'C는 m1으로 나타내는 경우 등이 있습니다.
일반적으로 진리표의 i번째 행에 해당되는 최소항을 mi라고 합니다.
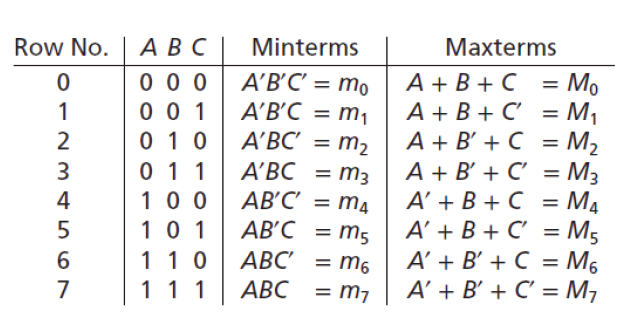
위 사진에서는 최대항(Maxterms)에 대해서도 나와있습니다. 눈치가 빠르다면 최대항에 대해서도 금방 눈치채셨겠지만, 우선은 최소항에 대해서 조금 더 언급할 것이 있어, 최대항은 조금 뒤에 다루도록 하겠습니다.
$$f = A'BC + AB'C' + AB'C + ABC' + ABC$$
위의 식처럼 함수 f가 최소항의 합으로 나타낼 수 있을 때, 최소항 전개(minterm expansion) 혹은 표준 논리곱의 합(standard sum of products)으로 되었다고 합니다.
진리표의 i번째 행에서 f = 1이면, mi = 1은 입력변수가 진리표의 i번째 행일 때이므로, mi는 최소항 전개에 나타나야 합니다.
f에 있는 최소항은 진리표에서 f가 1인 것과 일대일 대응을 하므로, 함수 f의 최소항 전개는 유일합니다.
저는 처음 공부할 때(사실 지금이 처음입니다만) 최소항 전개(혹은 표준 논리곱의 합)와 SOP(곱의 합)과 조금 헷갈렸습니다. 이에 대한 차이점은 다음과 같습니다.
SOP(sum-of-products, 곱의합)은 어떠한 식에 존재하는 모든 곱들이 단일 변수들의 곱으로 이루어져 있을 때, 이 식을 곱의합 형식이라고 합니다. 중요한 점은 각 항은 존재하는 모든 변수가 사용될 필요 없이, 단지 단일 변수들의 곱으로만 이루어져 있으면 된다는 것입니다.
그에 비해 최소항 전개(minterm expansion) 혹은 표준 논리곱의 합은 n개의 변수가 존재할 때, 식을 이루는 각 항들은 n개의 변수가 모두 단 한 번씩(보수 형태도 가능)나타나는 n개 문자로 이루어진, 즉 최소항들의 합으로 이루어진 식을 최소항 전개되었다고 합니다.
$$f = A'BC + AB'C' + AB'C + ABC' + ABC$$
위 식을 기호 m을 사용하여 나타내면 다음과 같습니다.
$$f(A, B, C) = m_3 + m_4 + m_5 + m_6 + m_7$$
이 식은 십진수를 나열하는 형식으로 더욱 간단하게 아래와 같이 표현할 수 있습니다.
$$f(A,B,C) = \sum_{}^{}m(3, 4, 5,6,7)$$
🌱 최대항(maxterm)
다음 식을 보도록 하겠습니다.
$$ f = (A + B + C)(A + B + C')(A + B' + C) $$
위 식의 각 항 각각을 최대항(maxterm)이라고 합니다.
일반적으로 n개의 변수의 최대항은 각 변수가 그대로 혹은 보수 형태로 한 번씩만 나타나는 n개 문자의 합입니다.

최대항은 보통 기호 M을 사용하여 간단하게 나타냅니다. 최소항과 마찬가지로 진리표의 i번째 행에 해당하는 최대항이 Mi입니다. 각 최대항은 대응하는 최소항의 보수와 같습니다. 즉 다음이 성립합니다.
$$M_i = m_i'$$
함수 f를 아래 식처럼 최대항의 곱으로 나타낼 때 이것을 최대항 전개(maxterm expansion) 혹은 표준 논리합의 곱(standard product of sum)이라 합니다.
$$ f = (A + B + C)(A + B + C')(A + B' + C) $$
위 식을 기호 M을 사용하여 간략화하면 다음과 같습니다.
$$ f(A,B,C) = M_0M_1M_2$$
이를 더욱 간단하게 아래와 같이 표현할 수 있습니다.
$$f(A,B,C) = \coprod M(0,1,2)$$
🧐 보수
f의 최소항 혹은 최대항 전개가 주어지면 f의 보수에 대한 최소항 혹은 최대항 전개는 쉽게 얻을 수 있습니다.
f'에 대한 최소항 전개는 f에 빠진 최소항들을 포함하면 됩니다.
예를 들어 $$f(A,B,C) = \sum_{}^{}m(3, 4, 5,6,7)$$ 가 주어졌을 때, f'에 대한 최소항 전개는 다음과 같습니다.
$$f'(A,B,C) = m_0 + m_1 + m_2 = \sum_{}^{}m(0,1,2)$$
또한 최소항의 보수는 최대항이므로
함수 f에 대한 최대항 전개(maxterm expansion)를 보수화 하면, 함수 f'에 대한 최소항 전개(minterm expansion)을 얻어낼 수 있습니다.
🌱 최소항 (혹은 최대항) 전개를 구하는 방법
최소항 전개를 얻기 위해서는 우선 논리곱의 합(sum of product)으로 식을 작성한 후, 각 항에서 빠진 변수를 X + X' = 1 정리를 사용하여 추가하는 것이다.
또한 f의 최대항을 구하는 방법은 f의 최소항에 해당하지 않는 십진 정수를 열거하여 구할 수 있다.
예를 들어 최소항에 m0, m1, m2, m3 이 사용되었다면, 최대항에는 M4, M5, ...가 사용되는 형식이다.
이 방법 말고도 최대항 전개를 구하는 방법은 다음과 같다.
논리합의 곱(products of sum)을 얻도록 f를 인수분해하고, XX'=0을 적용하여 각 합 항에서 빠진 변수를 추가하여 최대항들을 얻도록 다시 인수분해하는 것이다.
(a + c) -> (a+ bb' + c) -> (a + b + c)(a + b' + c)의 형식이다.
🧐 최소항과 최대항 전개의 일반화
아래 표는 세 변수의 일반 함수에 대한 질리표를 보여줍니다.
각 ai는 0 혹은 1의 값을 갖는 상수입니다.
| A B C | F |
| 0 0 0 | a0 |
| 0 0 1 | a1 |
| 0 1 0 | a2 |
| 0 1 1 | a3 |
| 1 0 0 | a4 |
| 1 0 1 | a5 |
| 1 1 0 | a6 |
| 1 1 1 | a7 |
위 표로부터 다음과 같이 세 변수의 일반 함수에 대하여 최소항 전개를 할 수 있습니다.
$$ F = a_0m_0 + a_1m_1 + \cdots + a_7m_7 = \sum_{i=0}^{7}a_im_i $$
ai = 1이면 최소항 mi는 전개에 포함되고, ai = 0이면 mi는 포함되지 않습는다.
최대항 전개는 다음과 같습니다.
$$F = (a_0 + M_0)(a_1 + M_1)\cdots(a_7+ M_7) = \coprod_{i=0}^{7}(a_i + M_i)$$
ai = 1 이면 ai + Mi = 1이므로 Mi는 전개에서 빠지지만, ai = 0이면 Mi는 들어갑니다.
또한 보수에 대해서는 다음과 같습니다.
보수에 대한 최소항 전개
$$F' = [\prod_{i=0}^{7}(a_i+M_i)]' = \sum_{i=0}^{7}a_i'M_i' = \sum_{i=0}^{7}a_i'm_i$$
보수에 대한 최대항 전개
$$F' = [\sum_{i=0}^{7}a_im_i]' = \prod_{i=0}^{7}(a_i'+m_i') = \prod_{i=0}^{7}(a_i'+M_i)$$
이를 변수의 개수가 n개인 상황으로 일반화하면 다음과 같습니다.
$$F = \sum_{i=0}^{2^{n}-1}a_im_i = \prod_{i=0}^{2^{n}-1}(a_i + M_i)$$
$$F' = \sum_{i=0}^{2^{n}-1}a_i'm_i = \prod_{i=0}^{2^{n}-1}(a_i' + M_i)$$
'🖥 Computer Science > 논리회로' 카테고리의 다른 글
| [논리회로] (5) - 카노맵 (Karnaugh map), 주항, 필수주항 (0) | 2022.03.27 |
|---|---|
| [논리회로] (4) - 비완전 명세함수 (0) | 2022.03.27 |
| [논리회로] (2) - 부울 대수 (Boolean algebra) (0) | 2022.03.26 |
| [논리회로] (1) - 2진수와 수 체계 (0) | 2022.03.26 |
| [논리회로] (0) - 디지털시스템과 논리설계, 스위칭 회로에 대하여 (0) | 2022.03.26 |
