디지털 시스템의 논리 설계를 학습하기 위해 필요한 기본 수학은 부울 대수이다.
우리가 사용할 모든 스위칭 장치들은 기본적으로 2상태 장치이며 따라서 우리는 모든 변수가 두 값 중 하나만을 가지는 부울 대수의 특별한 경우를 강조할 것이다.
이렇게 두 값을 갖는 부울 대수는 종종 스위칭 대수라고 불린다.
부울 대수에서 사용되는 0과 1은 수치적인 값을 가지지 않는다.
대신 논리회로에서 두 개의 다른 상태를 표현하고, 스위칭 변수의 두 값을 나타낸다.
논리 게이트 회로에서, 0을 일반적으로 낮은 전압대를 표현하고, 1은 높은 전압대를 표현한다.
스위칭 회로에서 0은 일반적으로 열린 회로(normally open, NO)를 의미하고, 1은 닫힌 회로(normally close, NC)를 의미한다.
🧐 기본 연산
부울(스위칭) 대수의 기본 연산은 AND, OR과 보수(혹은 반전, complement)이다.
🌱 보수(complement)
0의 보수는 1이고, 1의 보수는 0이다.
상징적으로는 다음과 같이 표현한다.
0' = 1 그리고 1' = 0
만약 X가 스위칭 변수라면
X = 0일 때 X' = 1 그리고 X = 1 일 때 X' = 0
보수화의 또 다른 이름은 반전(inversion)이다. X의 반전을 구성하는 전자회로는 인버터(inverter)이다.
인버터는 상직적으로 다음 기호로 표시하는데,

출력 쪽의 작은 원은 반전을 표시한다.
🌱 AND (논리곱)
어떤 일반적인 스위치 회로가 있을 때, 단자(terminal) 사이가 연결되지 않았으면 값 0이 할당되고, 단자가 연결되면 값 1이 할당된다.
이 스위칭 회로가 2개로만 구성되어 있다면 스위치는 직렬 혹은 병렬로 연결된다.
스위치 접점 A, B가 직렬로 연결되었을 때, A와 B중 하나만 열리거나 둘 다 열리게 된다면(0), 이는 열린 회로가 된다.
A와 B가 모두 연결이 되면(1), 이는 닫힌 회로가 된다.

이는 AND 연산을 정의하며, 대수적으로 C = A * B라 표기된다.
* 심볼은 부울식에서 종종 생략되므로 우리는 A * B 대신에 AB라고 표기할 것이다.
AND 연산은 논리곱으로 불린다.
🌱 OR (논리합)
스위치 A, B가 병렬로 연결되었을 때, A와 B중 하나라도 닫혀 있다면(1) 이는 닫힌 회로가 되고, A와 B 모두 열려(0) 있을 때만 열린 회로가 된다.
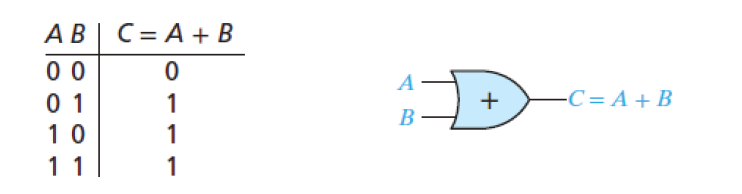
이는 OR 연산을 정의하며, 대수적으로 C = A + B라 표기한다.
🌱 Exclusive - OR (베타적 논리합)
베타적 논리합은 뒤에서 자세히 다룰 것이므로 진리표와 논리 게이트의 기호만 살펴보겠다.

🧐 부울 대수 기본 정리
다음은 부울 대수의 기본 법칙과 정리이다.
🌱 0과 1의 연산(operations with 0 and 1)
X + 0 = X X * 1 = X
X + 1 = 1 X * 0 = 0
🌱 멱등 법칙(indempotent laws)
X + X = X X*X = X
🌱 대합 법칙(involution laws)
(X')' = X
🌱 보수 법칙(laws of complementarity)
X + X' = 1 X * X' = 0
🔎 교환, 결합, 분배, 드모르간 법칙
🌱 AND, OR의 교환법칙
XY = YX X + Y = Y + X
🌱 AND, OR의 결합법칙
(XY)Z = X(YZ) = XYZ (X + Y) + Z= X + (Y + Z) = X + Y + Z
🌱 분배법칙(매우 중요)
X(Y + Z) = XY + XZ X + YZ = (X+Y)(X+Z)
우측의 식을 제2 분배법칙이라 칭한다.
일반 분배 법칙은 AND 연산이 OR 연산보다 우선이지만, 제2 분배법칙은 OR 연산이 AND 연산보다 우선이다.
제2 분배법칙은 부울식을 다루는 데 매우 유용하므로 꼭 알아두자.
🌱 드로르간의 법칙
(X + Y)' = X'Y' (XY)' = X' + Y'
🌱 쌍대(Duality)
부울 대수 법칙은 쌍대(duality)를 만족하는 대수를 보여주기 위해 둘씩 짝을 지어 보여진다.
부울 대수식이 주어지면, 상수 0과 1을 서로 바꾸고, AND와 OR 연산을 서로 바꾸어서 그 식의 쌍대를 구한다.
변수와 보수는 바꾸지 않고 놔둔다.
$$(XYZ...)^{D} = X + Y + Z + \cdots $$
$$(X + Y + Z + \cdots )^{D} = XYZ...$$
🧐 간략화 정리
🌱 연합(Uniting)
XY + XY' = X (X + Y)(X + Y') = X
🌱 흡수(absorption)
X + XY = X X(X + Y) = X
🌱 소거(elimination)
X + X'Y = X + Y X(X' + Y) = XY
🌱 합의(consensus)
XY + YZ + X'Z = XY + X'Z (X + Y)(Y + Z)(X' + Z) = (X + Y)(X' + Z)
합의 법칙은 XY + X'Z + (X + X')YZ로 두고 전개하여 증명할 수 있다.
🌱 Theorems for multiflying out and factoring (곱셈 전개과 인수화 정리)
(X + Y)(X' + Z) = XZ + X'Y XY + X'Z = (X + Z)(X' + Y)
(후에 배우겠지만, 곱의합과 합의곱을 얻기 위해 사용한다.)
🧐 곱셈 전개와 인수화
🌱 곱의합(sum-of-products, SOP)
곱의합(sum-of-products, SOP)을 얻기 위한 곱셈 전개를 하기 위해 두 개의 분배법칙이 사용된다.
모든 곱들이 단일 변수들의 곱으로 이루어져 있을 때 이 식을 곱의합 형식이라고 한다.
이 형식은 식이 완전히 곱셈 전개 되었을 때의 최종 결과이기도 하다.
곱의합 식은 곱셈 항들의 합 형태로 구성되어 있으므로 곱의합 식을 인식하는 것은 보통 쉬운 편이다.
AB' + CD'E + AC'E'
위와 같은 형식은 곱의 합 형식이지만, 아래 식은 곱의 합 형식이 아니다.
(A + B)CD + EF
곱셈항에 속한 (A + B) 항이 단일 변수가 아니기 때문이다.
식을 곱셈 전개할 때 가능하다면 제2 분배법칙을 먼저 적용해야 한다.
🌱 합의곱(products-of-sums, POS)
합의곱(product-of-sums, POS) 형식을 얻기 위해 식을 인수화하는 데, 두 가지 분배법칙 모두 사용될 수 있다.
모든 합들이 단일 변수들의 합일 때, 이 식을 합의곱 형식이라고 한다.
(A + B')(C + D' + E)(A + C' + E)
또한 아래도 여전히 합의곱 형식이다.
(A + B)(C + D + E)F
AB'C(D' + E)
그러나 아래는 합의곱 형식이 아니다.
(A + B)(C + D + E) + EF
추가로 다음 정리는 인수화와 곱셈 전개에 매우 유용하다.
(X+Y)(X' + Z) = XZ + X'Y
🧐 부울식 보수화
어떤 부울식의 반전 혹은 보수는 드모르간의 법칙을 적용함으로써 쉽게 구할 수 있다.
드모르간의 법칙은 다음과 같이 n 변수들로 쉽게 일반화할 수 있다.
$${}(X_1 + X_2 + X_3 + \cdots + X_n)' = {}(X_1)'{}(X_2)'{}(X_3)'...{}(X_n)'$$
$${}(X_1 X_2 X_3 ... X_n)' = {}X_1' + {}X_2' + {}X_3' + \cdots +{}X_n' $$
논리합으로서의 OR 연산과 논리곱으로서의 AND 연산을 고려하면 드모르간의 법칙은 다음과 같이 말할 수 있다.
곱의 보수는 보수들의 합이다.
합의 보수는 보수들의 곱이다.
추가로 어떤 식의 쌍대(Dual)는 전체 식을 보수화한 이후에, 각각의 개개 변수를 보수화하여 구한다.
예를 들어
$$AB' + C$$의 쌍대를 구하는 과정은 아래와 같다.
$$(AB'+C)' = (AB')'C' = (A' + B)C'$$
이고 따라서 쌍대는 다음과 같다.
$$(AB'+C)^{D} = (A+B')C$$
🧐 배타적 OR과 등가 연산
🌱 배타적 OR 연산(exclusive-OR, ⊕)
배타적 OR 연산은 다음과 같이 정의된다:
0⊕0=0, 0⊕1=1
1⊕0=1, 1⊕1=0
배타적 OR은 AND 와 OR의 항들로 표현될 수 있는데, 다음과 같다.
X ⊕ Y = X'Y + XY'
그리고 다음의 정리들이 배타적 OR에서 사용된다.
X ⊕ 0 = X
X ⊕ 1 = X'
X ⊕ X = 0
X ⊕ X' = 1
X ⊕ Y = Y ⊕ X
(X ⊕ Y) ⊕ Z = X ⊕ (Y ⊕ Z) = X ⊕ Y ⊕ Z
X(Y ⊕ Z) = XY ⊕ XZ
(X ⊕ Y)' = X ⊕ Y' = X' ⊕ Y = XY + X'Y'
또한 베타적 OR은 1의 개수가 홀수개일 때 결과값이 1인 홀수함수라 생각하면 편하다.
🌱 등가연산(equivalence operation, ≡)
등가연산은 다음과 같이 정의된다.
0≡0 = 1
0≡1 = 0
1≡0 = 0
1≡1 = 1
즉 등가는 배타적 OR의 보수이며, 다음이 성립한다.
X ≡ Y = XY + X'Y'
(X ≡ Y)' = (X ⊕ Y) 이므로
(XY + X'Y')' = XY' + X'Y
🧐 합의(consensus) 정리
합의 정리는 부울식을 간략화하는데 매우 유용하다.
XY + X'Z + YZ 형태의 식이 주어졌을 때, YZ항은 중복적이어서 소거될 수 있고, XY + X'Z 형태로 표현될 수 있다
소거된 항을 합의항(consensus term) 이라고 한다. 한 쪽 항에는 한 변수가, 다른쪽 항에는 그 변수의 보수가 있는 두 개의 항이 주어졌을 때, 합의항은 그 변수와 그 변수의 보수를 제외한 항을 곱해서 얻을 수 있다.
XY + YZ + X'Z = XY + X'Z (X + Y)(Y + Z)(X' + Z) = (X + Y)(X' + Z)
🧐 스위칭 식의 대수적 간략화
지금까지 배운 부울 대수 법칙과 정리를 사용하여, 스위칭 식을 간략화하기 위한 방법들을 복습하고 요약할 것이다.
1. 항들의 조합.
두 항을 조합하기 위해 정리 XY + XY' = X 를 이용해라
예를 들어 다음과 같은 식이 있다.
abc'd' + abcd' = abd' [ X = abd', Y = c ]
2. 항들의 소거
두 항을 소거하기 위해 정리 X + XY = X 를 이용해라.
예를 들어 다음과 같은 식이 있다.
a'b + a'bc = a'b
3. 문자들 소거
중복되는 문자를 소거하기 위해 정리 X + X'Y = X + Y를 이용하라.
이 정리를 적용하기 전에는 간단한 인수화가 필요할 수 있다.
1, 2, 3을 적용한 후에 더 이상 간략화를 할 수 없다면 중복항을 신중히 도입하는 것이 필요할 수도 있다.
4. 중복항 추가.
중복항은 xx'을 더하거나, (x + x')을 곱하거나, yz를 xy + x'z에 더하거나, xy를 x에 더하는 방법과 같은 방법으로 도입될 수 있다.
🧐 등식의 유효성 증명
변수값이 모든 조합에 대해 어떤 등식이 유효한지 아닌지를 결정하는 것이 종종 필요하다.
이럴 때 다음과 같은 방법들을 사용할 수 있다.
- 진리표를 만들어 모든 조합에 대해 등식의 양변을 평가한다.
- 등식의 한 변이 다른 변과 같아질 때까지 다양한 정리들을 적용한다.
- 등식의 양변 식이 같도록 축약한다.
- 가역적(reversible) 연산이 되는 등식의 양변에, 똑같은 연산을 수행하는 것이 허용된다. 예를 들면, 식의 양변에 보수를 취하는 것은 가능하지만, 양변에 같은 식을 곱하는 것은 허용되지 않는다.(부울 대수에서는 나눗셈의 정의되어 있지 않기 때문이다.) 유사하게, 뺄셈이 부울 대수에서 정의되지 않으므로 양변에 같은 항을 더하는 것은 허용되지 않는다.
'🖥 Computer Science > 논리회로' 카테고리의 다른 글
| [논리회로] (5) - 카노맵 (Karnaugh map), 주항, 필수주항 (0) | 2022.03.27 |
|---|---|
| [논리회로] (4) - 비완전 명세함수 (0) | 2022.03.27 |
| [논리회로] (3) - 최소항과 최대항 전개 (4) | 2022.03.27 |
| [논리회로] (1) - 2진수와 수 체계 (0) | 2022.03.26 |
| [논리회로] (0) - 디지털시스템과 논리설계, 스위칭 회로에 대하여 (0) | 2022.03.26 |
