🧐 Lower Bound
Upper Bound는 빅오 표기법을 사용해 보였다면 이미 아실 것이라 생각합니다.
Lower Bound 역시 이와 비슷합니다.
어떤 문제가 주어졌을 때, '해당 문제를 해결하는 알고리즘의 Lower Bound가 T이다.'의 의미는 다음과 같습니다.
(어떤 가정 하에서) 해당 문제를 T 시간보다 더 빨리 해결할 수 없다.
이때 가정은 계산 모델, 추가 사용 공간 등의 여러가지 가정이 있을 수 있습니다.
또한 빅-오메가(Ω) 표기법을 사용하여 표기합니다.
예시를 하나 살펴보겠습니다.
길이 n인 배열에서 최대값을 찾는 알고리즘의 lower bound는 Ω(1)이라고 표현할 수도 있고, Ω(n)이라 표현할 수도 있습니다.
이 경우 Ω(n)으로 나타내는 것이 더 우수한(유용한) Lower Bound가 됩니다.
🧐 Optimal Algorithm
어떤 문제를 해결하는 알고리즘의 Upper Bound와 Lower Bound가 일치하는 경우,
해당 Upper Bound를 가지는 알고리즘을 의미합니다.
어떤 문제를 T 시간 안에 해결하는 Optimal Algorithm의 존재를 증명하는 방법은 다음과 같습니다.
- T 시간 안에 문제를 해결하는 Algorithm을 디자인합니다. (이는 Upper Bound를 구하는 것과 같습니다.)
- 해당 알고리즘의 Lower Bound가 T임을 증명합니다.
🧐 Adversary Argument
Optimal Algorithm을 증명하기 위해서는 Lower Bound를 구하는 방법이 필요합니다.
Adversary Argument는 Lower Bound를 증명할 수 있는 여러 방법들 중 하나의 방법입니다.
Adversay Argument는 Solver와 Adversary간에 이루어지는 스무고개 게임과 비슷한 느낌의 게임이라 생각할 수 있습니다.
진행은 다음과 같이 이루어집니다.
Adversary는 input(정답)을 가지고 있으며, solver는 해당 input이 무엇인지 확인할 수 없지만 Adversary에게 질문을 할 수는 있습니다.
(질문의 형식 제약은 계산 모델의 제약과 동일합니다.)
Adversary는 Solver의 질문에 대해 대답을 해야 하며, Solver가 문제를 해결하기 어렵게 하기 위해 input을 계속 바꿀 수 있습니다.
그러나 input을 바꿀 때에는 이전의 질문에 대한 답변에 대하여 일관성(Consistently)을 유지해야 합니다.
Algorithm의 Lower Bound는 Solver에게 필요한 최소한의 질문 횟수가 됩니다.
몇 가지 예시들을 통해 살펴보도록 하겠습니다.
🧐 예시 1 : 최댓값 위치 찾기
Problem : Array[1, .., 5] 에서 Maximum Element의 위치 찾기
배열의 인덱스는 1부터 시작하고, Array의 각 Element는 모두 다르다고 가정하겠습니다.
질문의 형식(계산 모델)은 다음과 같습니다.
A의 i번째 element는 j번째 element보다 큰가?
(A[i] > A[j])
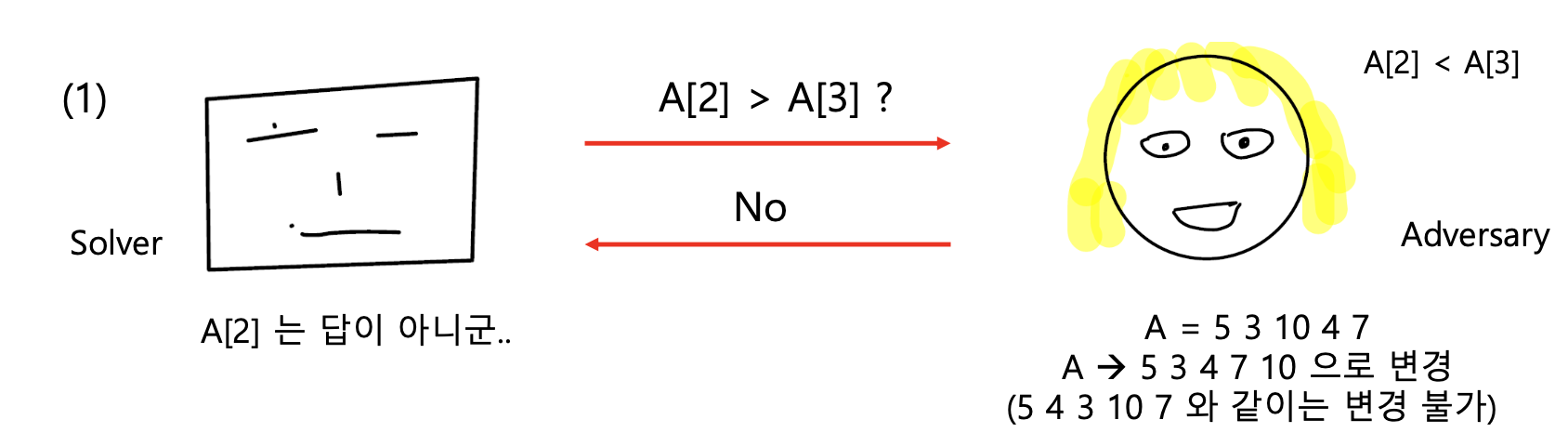
3번째 요소가 2번째 요소보다 크다고 대답을 했으므로, input을 5, 4, 3, 10, 7로 바꾼 경우 해당 대답에 모순이 됩니다.
따라서 이와 같이는 바꿀 수 없습니다.
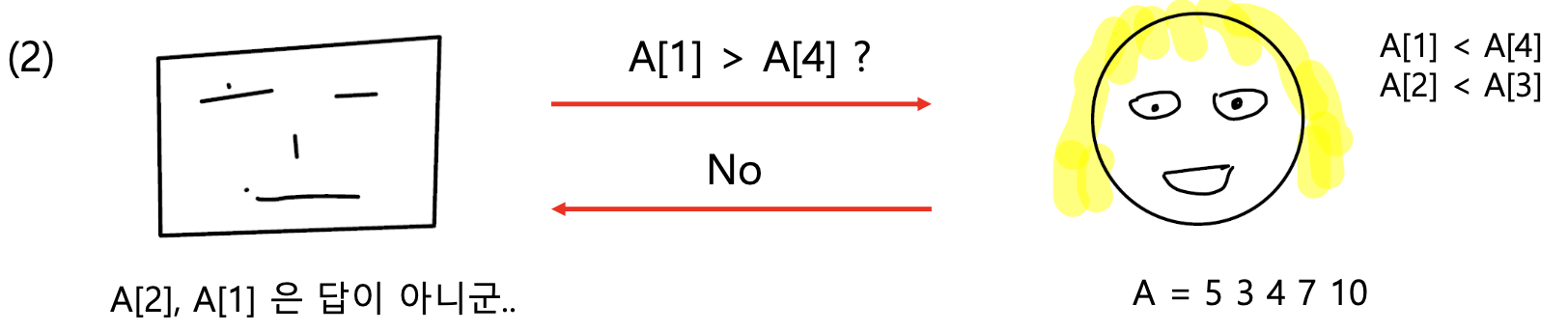
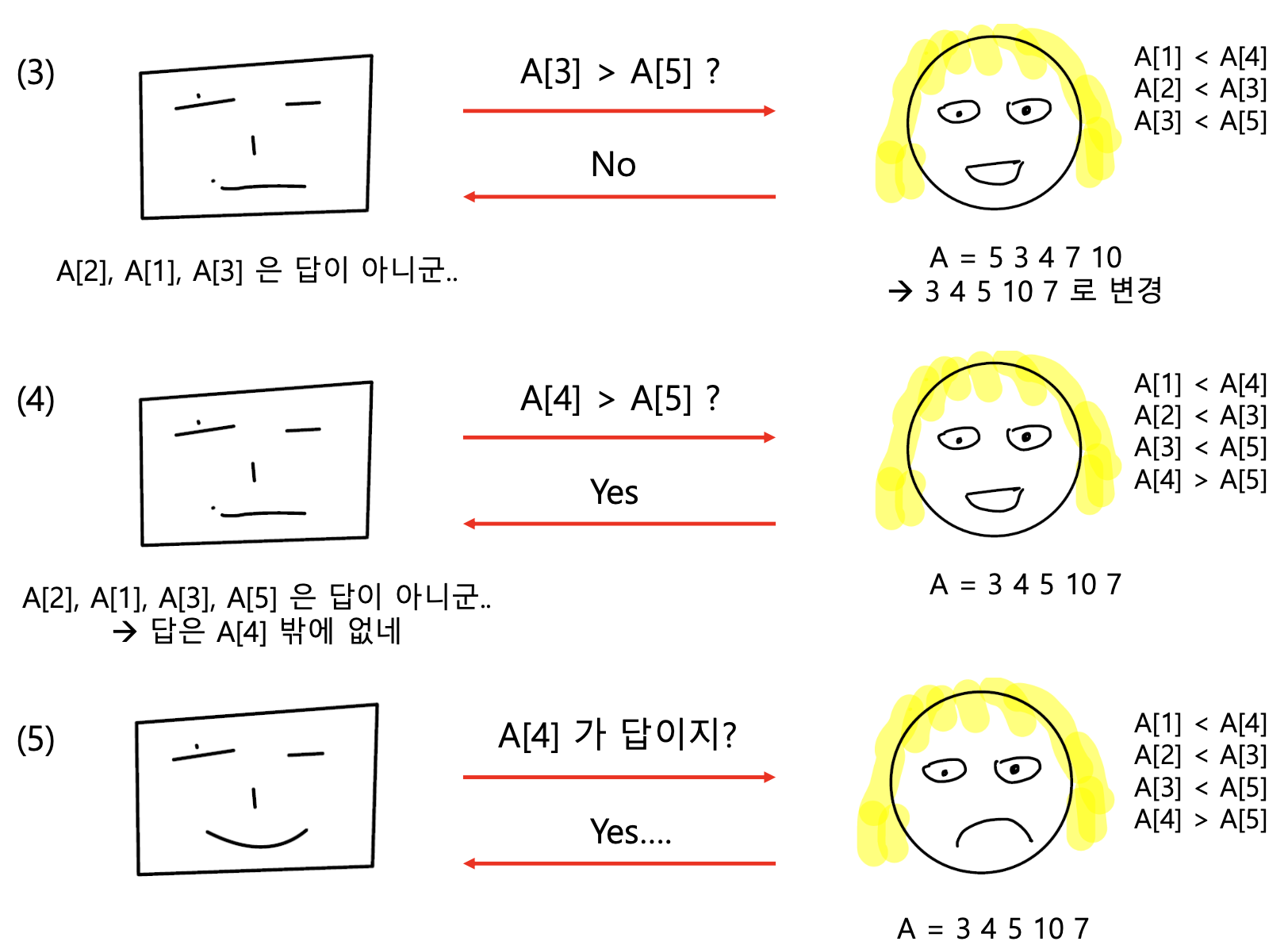
즉 이를 통해 Solver는 최소 4번의 질문이 필요함을 알 수 있으며, 이를 통해 해당 Problem의 Lower Bound는 4라는 것을 알 수 있습니다.
만약 4번보다 적게 비교한다면 대소관계를 알 수 없는 두 개 이상의 Element가 존재하게 되며, Adversary는 해당 Element를 임의로 바꿈으로써 정답을 맞추지 못하게 할 수 있습니다.
🧐 예시 1의 변형 : 최댓값 위치 찾기
위 과정을 다음과 같이 다시 표현해 보도록 하겠습니다.
우선 Directed Graph를 하나 정의하도록 하겠습니다.
G = (V, E)
V = {1, 2, 3, 4, 5}
E = A[i] > A[j] 라는 대답을 Adversary에게 받을 때마다 edge(j, i)를 E에 추가.
따라서 G의 edge의 개수 = 현재까지 수행한 비교 횟수
예를 들어 3번의 질문을 통해
A[1] < A[4],
A[2] < A[3],
A[3] < A[5] 라는 대답을 받았다고 하면, 다음과 같습니다.

이때 Solver가 답을 하기 위해서는 최소 4개의 edge가 필요하다는 것을 알 수 있습니다.
그렇지 않다면 최소 두개의 Connected Component가 생성되고,
서로 다른 두 Component에 속한 두 정점(위의 예시에서는 A[4]와 A[5])을 Adversary가 마음대로 바꿀 수 있습니다.
(A[4]와 A[5] 사이에는 아무런 topology가 존재하지 않기 때문입니다.)
이와 같은 방법으로 Size n인 array의 경우 n-1이 Lower Bound인 것을 증명할 수 있습니다.
🧐 또다른 방법 : 최댓값 위치 찾기
Adversary Argument를 이용하되, 다른 방법으로 Lower Bound를 증명해 보도록 하겠습니다.
Adversary에 의하여 A[j] > A[i]라고 판명된 경우, j는 i를 이김(i는 j에게 짐)이라고 한 뒤, Array Position Set({1, 2, 3, 4, 5})을 다음과 같이 세 개의 집합으로 Partition 하도록 하겠습니다.
W : 한 번 이상 이겼으며, 한 번도 지지 않은 position들의 집합
L : 한 번 이상 진 position들의 집합
N : 한 번도 비교하지 않은 position들의 집합
정의에 의해 초기 상태는 W와 L은 ∅(공집합)이며, N = {1, 2, 3, 4, 5}입니다.
N이 ∅이고, L의 크기가 n-1인 경우 W에 존재하는 유일한 position이 최댓값의 position이 됩니다.
N의 크기가 1 줄거나, L의 크기가 1 증가할 때마다 1 credit을 얻는다고 가정하면, 문제를 해결하기 위해서는 최소 4 x 2 + 1 = 9 credit이 필요합니다.
이제 질문에 대하여 얻을 수 있는 최소 credit을 정리한 표를 살펴보도록 하겠습니다.
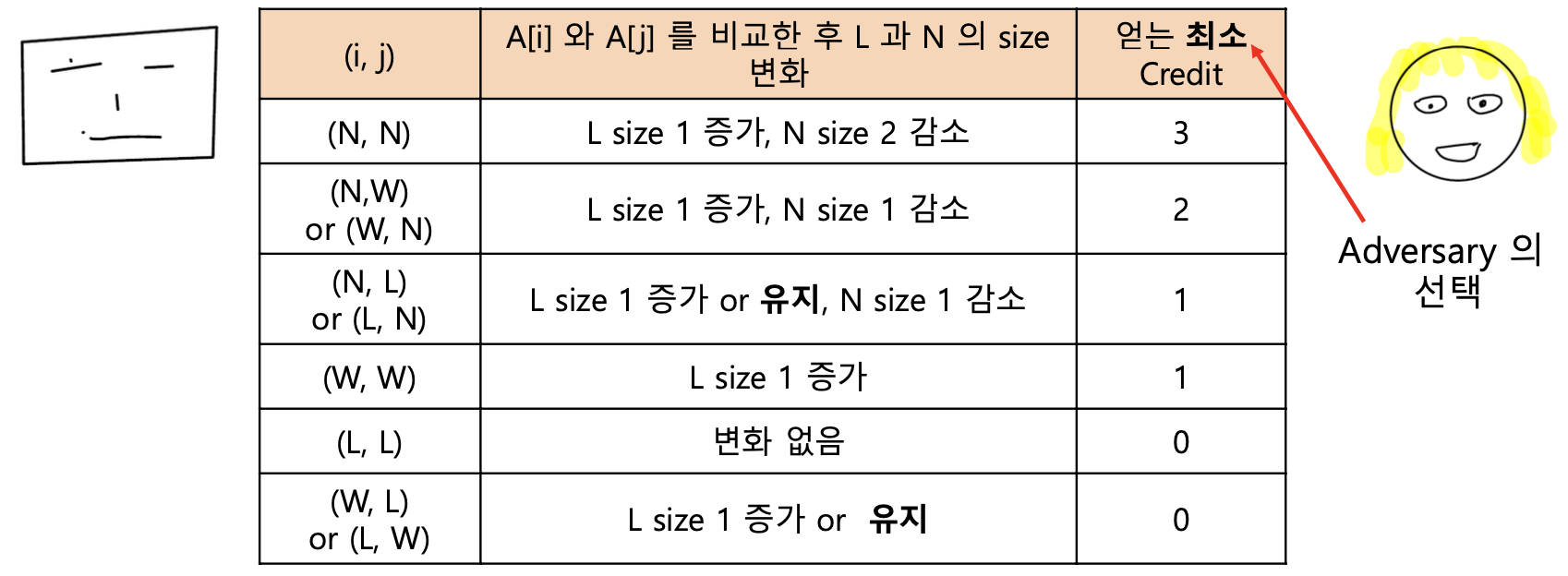
가능한 최소한의 연산으로 9 credit을 벌기 위해 Solver는 많은 Credit을 주는 것 부터 Greedy하게 선택할 수 있습니다.
즉 처음 두 번은 (N ,N)에 위치한 두 position을 비교합니다. (6 credit)
위 두 번의 비교가 끝난 경우, N에는 하나의 원소만이 존재하기 때문에, (N, N) 비교를 또다시 진행할 수는 없습니다.
즉 이후에는 다른 연산들만을 수행해야 하며, 9 credit을 벌기 위해서는 최소 4번의 질문이 필요하다는 것을 알 수 있습니다.
만약 size n인 array에 대하여, 문제를 해결하기 위해서는 $(n-1) \times 2 + 1 = 2n - 1$ credit이 필요하며 (N, N)비교는 $\left \lfloor \frac{n}{2} \right \rfloor$ 번 만이 가능합니다.
따라서 $3 \times \left \lfloor \frac{n}{2} \right \rfloor$ credit을 얻을 수 있습니다.
이후에는 짝수의 경우 N에 더이상 남아있는 원소가 없으므로 credit 1을 주는 비교(W, W)만을 수행할 수 있고,
따라서 $\frac{n}{2} - 1$ 번의 추가 연산이 필요합니다.
홀수의 경우 N에는 원소가 하나 남으므로 credit 2를 주는 비교를 1회 수행할 수 있으며,
이후 credit 1을 주는 연산(W, W)을 $\left \lfloor \frac{n}{2} \right \rfloor - 1$ 번 더 수행해야 합니다.
따라서 두 경우 모두 lower bound가 n-1입니다.
🧐 예시 2 : 최댓값과 최솟값 위치 찾기
위의 예시를 조금 더 확장시켜, 해당 문제를 생각해 보도록 하겠습니다.
Problem : 길이 n인 배열 A[1, ..., n] 에서 최댓값과 최솟값의 position을 찾기.
우선 기본적으로 생각할 수 있는 방법은 최댓값과 최솟값을 각각 n-1번의 비교에 걸쳐 찾는 방법을 생각할 수 있습니다.
이 경우 비교 횟수는 2(n-1) 입니다.
그러나 최댓값을 찾은 후, 최댓값을 제외한 요소들 중에서 최솟값을 찾는다면 n-1 + n-2 = 2n -3번의 비교 횟수면 충분합니다.
조금 더 성능을 향상시켜본다면, 모든 n보다 작은 홀수 i에 대하여, A[i]와 A[i+1]을 비교한 후 W와 L을 각각 다음과 같은 집합으로 정의하겠습니다.
W : 둘 중 더 큰 값을 저장한 위치
L : 둘 중 더 작은 값을 저장한 위치
W에 속한 position들 중 가장 큰 값을 저장한 position과, L에 속한 position들 중 가장 작은 값을 저장한 position이 각각 최댓값의 위치와 최솟값의 위치가 됩니다.
이 경우 총 비교 횟수는 $\frac{n}{2} + \frac{n}{2} - 1 + \frac{n}{2} - 1 = \frac{3n}{2}-2$ 입니다.
위 알고리즘이 Optimal Algorithm인지 알아보기 위해 Adversary Argument를 사용하여 Lower Bound를 구해보도록 하겠습니다.
앞서 Find Max의 경우와 마찬가지로, Credit을 이용해서 증명할 수 있습니다.
이번에는 A의 position들의 집합을 다음 4개의 집합으로 partition하도록 하겠습니다.
U : 한 번도 비교하지 않은 Position들의 집합
W : 한 번도 지지 않은 Position들의 집합
L : 한 번도 이기지 못한 Position들의 집합
N : 한 번 이상 이기고, 한 번 이상 진 Position들의 집합
Solver에게 주어진 초기 상태는 U = {1, 2, ..., n} 이며, W와 L, N 은 ∅(공집합)입니다.
|U| = 0, |W| = |L| = 1, |N| = n-2 일 때 solver는 무조건 정답을 맞출 수 있습니다.
이제 어떤 position이 한 집합에서 다른 집합으로 옮겨지는 경우 1credit을 얻는다고 하겠습니다.
이때 어떤 position이 집합 N에 가기 위해서는 반드시 set W나 L을 거쳐가야 합니다. (즉 2 credit이 필요합니다.)
따라서 solver가 대답하기 위해서는 적어도 2(n - 2) + 2(U에서 W, U에서 L 1번 씩) = 2n - 2 credit이 필요합니다.
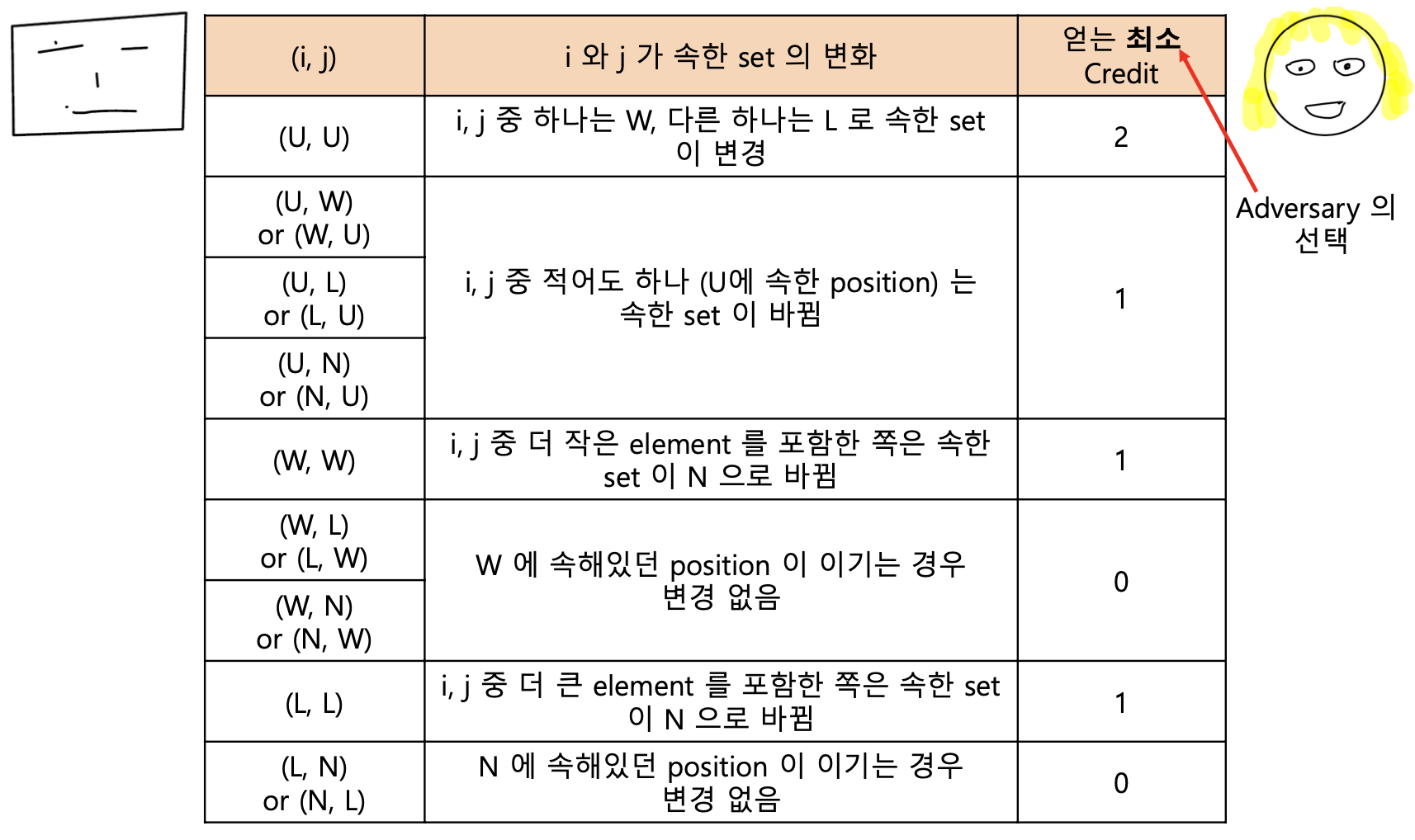
Solver는 (U, U)비교를 최대 $\frac{n}{2}$ 번 수행할 수 있습니다. 즉 이를 통해 n credit을 얻을 수 있습니다.
이제 2n - 2 - n = n - 2 credit이 남았는데, 이 경우 U에 속한 두 position이 존재하지 않기 때문에 Solver는 아무리 최적의 비교를 하더라도 1번 비교에 1 credit밖에 얻지 못합니다.
따라서 나머지 n-2 credit을 얻기 위해서는 최소한 n - 2번의 비교가 필요합니다.
즉 문제를 해결하기 위해서는 최소 $\frac{n}{2} + (n- 2) = \frac{3n}{2} -2$ 번의 비교가 필요합니다.
🧐 예시 3 : Comparision Based Sortiong
Problem : Comparison model 하에서 길이 n인 배열 A[1, 2, ..., n]을 sorting 하기
편의상 A의 모든 Element는 서로 다르다고 하겠습니다.
👉 comparision model
두 위치(position) i, j에 대하여, A[i]와 A[j]를 비교하여, 'A[i] > A[j]' 혹은 'A[i] < A[j]'의 답을 얻는 연산과,
두 위치를 swap하는 연산만이 가능하며,
다른 모든 연산은 사용 불가능한 model을 의미합니다.
👉 Upper Bound
Comparision-Based Sorting의 Upper Bound는 O(n log n) 입니다.
In-place heap sort를 사용하여 가능합니다.
👉 Lower Bound
편의를 위해 A를 아래와 같이 1에서 n까지의 순열(permutation) P[1, 2, ..., n]으로 변환하겠습니다.
이때 P[i] = j가 의미하는 것은 A[i]는 A에서 j번째로 작은 수임을 의미합니다.


이 경우 A를 sorting 하는 문제는 P를 구하는 문제와 동일해집니다.
이제 Lower Bound를 구하기 위해 다음과 같은 Full Binary Decision Tree를 정의하겠습니다.
Decision Tree의 non-leaf node들은 comparision 연산을 나타냅니다.
Decision Tree의 leaf node 들은 특정 permutation을 나타냅니다.
Decision Tree의 Root로부터 non-leaf node에 존재하는 comparison의 결과에 따라 두 간선 중 하나를 선택하여 아래로 내려가게 되며, 마지막 leaf node에 있는 permutation은 root로부터 수행했던 comparison의 대답을 모두 만족해야 합니다.
예를 들어 길이 3 permutation의 결정 트리는 아래와 같습니다.
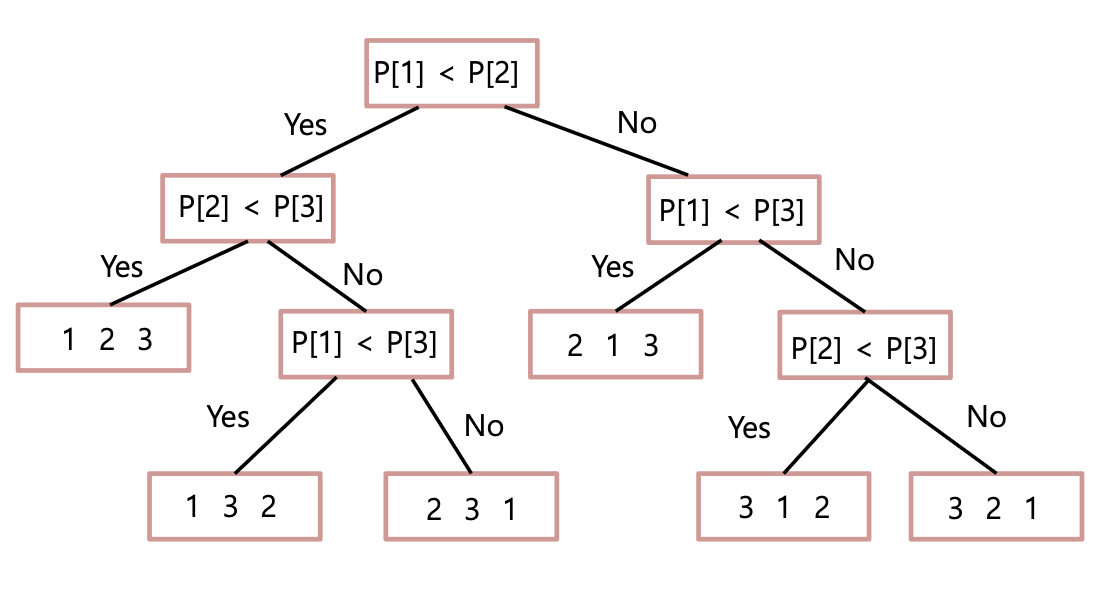
이에 대하여 Adversary Argument를 적용할 수 있습니다.
Decision Tree의 root에서 출발하여 각 node에 해당하는 질문을 Solver가 한 뒤, Solver는 해당 질문의 답에 따라 이동한 subtree에 속한 leaf node들 중 하나가 답이라는 것을 알 수 있습니다.
반대로 Adversary는 해당 subtree에 속한 leaf node들 중에 하나로 input을 변경할 수 있습니다.
결국 Solver가 정확하게 답을 알기 위해서는 decision tree의 subtree의 size가 1이 될 때 까지(즉 leaf node에 도달할 때까지) 계속해서 질문을 해야 합니다.
즉 Lower Bound는 Decision Tree의 최대 Depth가 됩니다.
Decision Tree의 Leaf node의 수 = P의 모든 경우의 수 = n!
Depth가 d인 binary tree는 최대 $2^d$ 개의 leaf node를 가질 수 있으므로, Decision Tree의 depth는 최소 log(n!)이 되어야 합니다.
n! ~ O($n^n$)을 사용하여 decision tree의 depth는 매우 큰 n에 대하여 Ω(n log n)이 됨을 알 수 있습니다.
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] Reduction (0) | 2022.12.05 |
|---|---|
| [알고리즘] Counting Sort (계수 정렬) (0) | 2022.12.05 |
| [알고리즘] DP(4) - 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2022.11.13 |
| [알고리즘] DP (3) - 벨만포드(Bellman-Ford) 알고리즘 (0) | 2022.11.12 |
| [알고리즘] DP (2) - Edit Distance(편집 거리) (0) | 2022.11.12 |
🧐 Lower Bound
Upper Bound는 빅오 표기법을 사용해 보였다면 이미 아실 것이라 생각합니다.
Lower Bound 역시 이와 비슷합니다.
어떤 문제가 주어졌을 때, '해당 문제를 해결하는 알고리즘의 Lower Bound가 T이다.'의 의미는 다음과 같습니다.
(어떤 가정 하에서) 해당 문제를 T 시간보다 더 빨리 해결할 수 없다.
이때 가정은 계산 모델, 추가 사용 공간 등의 여러가지 가정이 있을 수 있습니다.
또한 빅-오메가(Ω) 표기법을 사용하여 표기합니다.
예시를 하나 살펴보겠습니다.
길이 n인 배열에서 최대값을 찾는 알고리즘의 lower bound는 Ω(1)이라고 표현할 수도 있고, Ω(n)이라 표현할 수도 있습니다.
이 경우 Ω(n)으로 나타내는 것이 더 우수한(유용한) Lower Bound가 됩니다.
🧐 Optimal Algorithm
어떤 문제를 해결하는 알고리즘의 Upper Bound와 Lower Bound가 일치하는 경우,
해당 Upper Bound를 가지는 알고리즘을 의미합니다.
어떤 문제를 T 시간 안에 해결하는 Optimal Algorithm의 존재를 증명하는 방법은 다음과 같습니다.
- T 시간 안에 문제를 해결하는 Algorithm을 디자인합니다. (이는 Upper Bound를 구하는 것과 같습니다.)
- 해당 알고리즘의 Lower Bound가 T임을 증명합니다.
🧐 Adversary Argument
Optimal Algorithm을 증명하기 위해서는 Lower Bound를 구하는 방법이 필요합니다.
Adversary Argument는 Lower Bound를 증명할 수 있는 여러 방법들 중 하나의 방법입니다.
Adversay Argument는 Solver와 Adversary간에 이루어지는 스무고개 게임과 비슷한 느낌의 게임이라 생각할 수 있습니다.
진행은 다음과 같이 이루어집니다.
Adversary는 input(정답)을 가지고 있으며, solver는 해당 input이 무엇인지 확인할 수 없지만 Adversary에게 질문을 할 수는 있습니다.
(질문의 형식 제약은 계산 모델의 제약과 동일합니다.)
Adversary는 Solver의 질문에 대해 대답을 해야 하며, Solver가 문제를 해결하기 어렵게 하기 위해 input을 계속 바꿀 수 있습니다.
그러나 input을 바꿀 때에는 이전의 질문에 대한 답변에 대하여 일관성(Consistently)을 유지해야 합니다.
Algorithm의 Lower Bound는 Solver에게 필요한 최소한의 질문 횟수가 됩니다.
몇 가지 예시들을 통해 살펴보도록 하겠습니다.
🧐 예시 1 : 최댓값 위치 찾기
Problem : Array[1, .., 5] 에서 Maximum Element의 위치 찾기
배열의 인덱스는 1부터 시작하고, Array의 각 Element는 모두 다르다고 가정하겠습니다.
질문의 형식(계산 모델)은 다음과 같습니다.
A의 i번째 element는 j번째 element보다 큰가?
(A[i] > A[j])

3번째 요소가 2번째 요소보다 크다고 대답을 했으므로, input을 5, 4, 3, 10, 7로 바꾼 경우 해당 대답에 모순이 됩니다.
따라서 이와 같이는 바꿀 수 없습니다.


즉 이를 통해 Solver는 최소 4번의 질문이 필요함을 알 수 있으며, 이를 통해 해당 Problem의 Lower Bound는 4라는 것을 알 수 있습니다.
만약 4번보다 적게 비교한다면 대소관계를 알 수 없는 두 개 이상의 Element가 존재하게 되며, Adversary는 해당 Element를 임의로 바꿈으로써 정답을 맞추지 못하게 할 수 있습니다.
🧐 예시 1의 변형 : 최댓값 위치 찾기
위 과정을 다음과 같이 다시 표현해 보도록 하겠습니다.
우선 Directed Graph를 하나 정의하도록 하겠습니다.
G = (V, E)
V = {1, 2, 3, 4, 5}
E = A[i] > A[j] 라는 대답을 Adversary에게 받을 때마다 edge(j, i)를 E에 추가.
따라서 G의 edge의 개수 = 현재까지 수행한 비교 횟수
예를 들어 3번의 질문을 통해
A[1] < A[4],
A[2] < A[3],
A[3] < A[5] 라는 대답을 받았다고 하면, 다음과 같습니다.

이때 Solver가 답을 하기 위해서는 최소 4개의 edge가 필요하다는 것을 알 수 있습니다.
그렇지 않다면 최소 두개의 Connected Component가 생성되고,
서로 다른 두 Component에 속한 두 정점(위의 예시에서는 A[4]와 A[5])을 Adversary가 마음대로 바꿀 수 있습니다.
(A[4]와 A[5] 사이에는 아무런 topology가 존재하지 않기 때문입니다.)
이와 같은 방법으로 Size n인 array의 경우 n-1이 Lower Bound인 것을 증명할 수 있습니다.
🧐 또다른 방법 : 최댓값 위치 찾기
Adversary Argument를 이용하되, 다른 방법으로 Lower Bound를 증명해 보도록 하겠습니다.
Adversary에 의하여 A[j] > A[i]라고 판명된 경우, j는 i를 이김(i는 j에게 짐)이라고 한 뒤, Array Position Set({1, 2, 3, 4, 5})을 다음과 같이 세 개의 집합으로 Partition 하도록 하겠습니다.
W : 한 번 이상 이겼으며, 한 번도 지지 않은 position들의 집합
L : 한 번 이상 진 position들의 집합
N : 한 번도 비교하지 않은 position들의 집합
정의에 의해 초기 상태는 W와 L은 ∅(공집합)이며, N = {1, 2, 3, 4, 5}입니다.
N이 ∅이고, L의 크기가 n-1인 경우 W에 존재하는 유일한 position이 최댓값의 position이 됩니다.
N의 크기가 1 줄거나, L의 크기가 1 증가할 때마다 1 credit을 얻는다고 가정하면, 문제를 해결하기 위해서는 최소 4 x 2 + 1 = 9 credit이 필요합니다.
이제 질문에 대하여 얻을 수 있는 최소 credit을 정리한 표를 살펴보도록 하겠습니다.

가능한 최소한의 연산으로 9 credit을 벌기 위해 Solver는 많은 Credit을 주는 것 부터 Greedy하게 선택할 수 있습니다.
즉 처음 두 번은 (N ,N)에 위치한 두 position을 비교합니다. (6 credit)
위 두 번의 비교가 끝난 경우, N에는 하나의 원소만이 존재하기 때문에, (N, N) 비교를 또다시 진행할 수는 없습니다.
즉 이후에는 다른 연산들만을 수행해야 하며, 9 credit을 벌기 위해서는 최소 4번의 질문이 필요하다는 것을 알 수 있습니다.
만약 size n인 array에 대하여, 문제를 해결하기 위해서는 $(n-1) \times 2 + 1 = 2n - 1$ credit이 필요하며 (N, N)비교는 $\left \lfloor \frac{n}{2} \right \rfloor$ 번 만이 가능합니다.
따라서 $3 \times \left \lfloor \frac{n}{2} \right \rfloor$ credit을 얻을 수 있습니다.
이후에는 짝수의 경우 N에 더이상 남아있는 원소가 없으므로 credit 1을 주는 비교(W, W)만을 수행할 수 있고,
따라서 $\frac{n}{2} - 1$ 번의 추가 연산이 필요합니다.
홀수의 경우 N에는 원소가 하나 남으므로 credit 2를 주는 비교를 1회 수행할 수 있으며,
이후 credit 1을 주는 연산(W, W)을 $\left \lfloor \frac{n}{2} \right \rfloor - 1$ 번 더 수행해야 합니다.
따라서 두 경우 모두 lower bound가 n-1입니다.
🧐 예시 2 : 최댓값과 최솟값 위치 찾기
위의 예시를 조금 더 확장시켜, 해당 문제를 생각해 보도록 하겠습니다.
Problem : 길이 n인 배열 A[1, ..., n] 에서 최댓값과 최솟값의 position을 찾기.
우선 기본적으로 생각할 수 있는 방법은 최댓값과 최솟값을 각각 n-1번의 비교에 걸쳐 찾는 방법을 생각할 수 있습니다.
이 경우 비교 횟수는 2(n-1) 입니다.
그러나 최댓값을 찾은 후, 최댓값을 제외한 요소들 중에서 최솟값을 찾는다면 n-1 + n-2 = 2n -3번의 비교 횟수면 충분합니다.
조금 더 성능을 향상시켜본다면, 모든 n보다 작은 홀수 i에 대하여, A[i]와 A[i+1]을 비교한 후 W와 L을 각각 다음과 같은 집합으로 정의하겠습니다.
W : 둘 중 더 큰 값을 저장한 위치
L : 둘 중 더 작은 값을 저장한 위치
W에 속한 position들 중 가장 큰 값을 저장한 position과, L에 속한 position들 중 가장 작은 값을 저장한 position이 각각 최댓값의 위치와 최솟값의 위치가 됩니다.
이 경우 총 비교 횟수는 $\frac{n}{2} + \frac{n}{2} - 1 + \frac{n}{2} - 1 = \frac{3n}{2}-2$ 입니다.
위 알고리즘이 Optimal Algorithm인지 알아보기 위해 Adversary Argument를 사용하여 Lower Bound를 구해보도록 하겠습니다.
앞서 Find Max의 경우와 마찬가지로, Credit을 이용해서 증명할 수 있습니다.
이번에는 A의 position들의 집합을 다음 4개의 집합으로 partition하도록 하겠습니다.
U : 한 번도 비교하지 않은 Position들의 집합
W : 한 번도 지지 않은 Position들의 집합
L : 한 번도 이기지 못한 Position들의 집합
N : 한 번 이상 이기고, 한 번 이상 진 Position들의 집합
Solver에게 주어진 초기 상태는 U = {1, 2, ..., n} 이며, W와 L, N 은 ∅(공집합)입니다.
|U| = 0, |W| = |L| = 1, |N| = n-2 일 때 solver는 무조건 정답을 맞출 수 있습니다.
이제 어떤 position이 한 집합에서 다른 집합으로 옮겨지는 경우 1credit을 얻는다고 하겠습니다.
이때 어떤 position이 집합 N에 가기 위해서는 반드시 set W나 L을 거쳐가야 합니다. (즉 2 credit이 필요합니다.)
따라서 solver가 대답하기 위해서는 적어도 2(n - 2) + 2(U에서 W, U에서 L 1번 씩) = 2n - 2 credit이 필요합니다.

Solver는 (U, U)비교를 최대 $\frac{n}{2}$ 번 수행할 수 있습니다. 즉 이를 통해 n credit을 얻을 수 있습니다.
이제 2n - 2 - n = n - 2 credit이 남았는데, 이 경우 U에 속한 두 position이 존재하지 않기 때문에 Solver는 아무리 최적의 비교를 하더라도 1번 비교에 1 credit밖에 얻지 못합니다.
따라서 나머지 n-2 credit을 얻기 위해서는 최소한 n - 2번의 비교가 필요합니다.
즉 문제를 해결하기 위해서는 최소 $\frac{n}{2} + (n- 2) = \frac{3n}{2} -2$ 번의 비교가 필요합니다.
🧐 예시 3 : Comparision Based Sortiong
Problem : Comparison model 하에서 길이 n인 배열 A[1, 2, ..., n]을 sorting 하기
편의상 A의 모든 Element는 서로 다르다고 하겠습니다.
👉 comparision model
두 위치(position) i, j에 대하여, A[i]와 A[j]를 비교하여, 'A[i] > A[j]' 혹은 'A[i] < A[j]'의 답을 얻는 연산과,
두 위치를 swap하는 연산만이 가능하며,
다른 모든 연산은 사용 불가능한 model을 의미합니다.
👉 Upper Bound
Comparision-Based Sorting의 Upper Bound는 O(n log n) 입니다.
In-place heap sort를 사용하여 가능합니다.
👉 Lower Bound
편의를 위해 A를 아래와 같이 1에서 n까지의 순열(permutation) P[1, 2, ..., n]으로 변환하겠습니다.
이때 P[i] = j가 의미하는 것은 A[i]는 A에서 j번째로 작은 수임을 의미합니다.


이 경우 A를 sorting 하는 문제는 P를 구하는 문제와 동일해집니다.
이제 Lower Bound를 구하기 위해 다음과 같은 Full Binary Decision Tree를 정의하겠습니다.
Decision Tree의 non-leaf node들은 comparision 연산을 나타냅니다.
Decision Tree의 leaf node 들은 특정 permutation을 나타냅니다.
Decision Tree의 Root로부터 non-leaf node에 존재하는 comparison의 결과에 따라 두 간선 중 하나를 선택하여 아래로 내려가게 되며, 마지막 leaf node에 있는 permutation은 root로부터 수행했던 comparison의 대답을 모두 만족해야 합니다.
예를 들어 길이 3 permutation의 결정 트리는 아래와 같습니다.

이에 대하여 Adversary Argument를 적용할 수 있습니다.
Decision Tree의 root에서 출발하여 각 node에 해당하는 질문을 Solver가 한 뒤, Solver는 해당 질문의 답에 따라 이동한 subtree에 속한 leaf node들 중 하나가 답이라는 것을 알 수 있습니다.
반대로 Adversary는 해당 subtree에 속한 leaf node들 중에 하나로 input을 변경할 수 있습니다.
결국 Solver가 정확하게 답을 알기 위해서는 decision tree의 subtree의 size가 1이 될 때 까지(즉 leaf node에 도달할 때까지) 계속해서 질문을 해야 합니다.
즉 Lower Bound는 Decision Tree의 최대 Depth가 됩니다.
Decision Tree의 Leaf node의 수 = P의 모든 경우의 수 = n!
Depth가 d인 binary tree는 최대 $2^d$ 개의 leaf node를 가질 수 있으므로, Decision Tree의 depth는 최소 log(n!)이 되어야 합니다.
n! ~ O($n^n$)을 사용하여 decision tree의 depth는 매우 큰 n에 대하여 Ω(n log n)이 됨을 알 수 있습니다.
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] Reduction (0) | 2022.12.05 |
|---|---|
| [알고리즘] Counting Sort (계수 정렬) (0) | 2022.12.05 |
| [알고리즘] DP(4) - 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2022.11.13 |
| [알고리즘] DP (3) - 벨만포드(Bellman-Ford) 알고리즘 (0) | 2022.11.12 |
| [알고리즘] DP (2) - Edit Distance(편집 거리) (0) | 2022.11.12 |