🧐 Edit Distance
어떤 단어와 비슷한(가까운) 단어는 어떻게 정의할 수 있을까요?
예를 들어 Word의 spell check 기능을 보면 다음과 같이 비슷한 단어들을 알려주는 것을 알 수 있습니다.
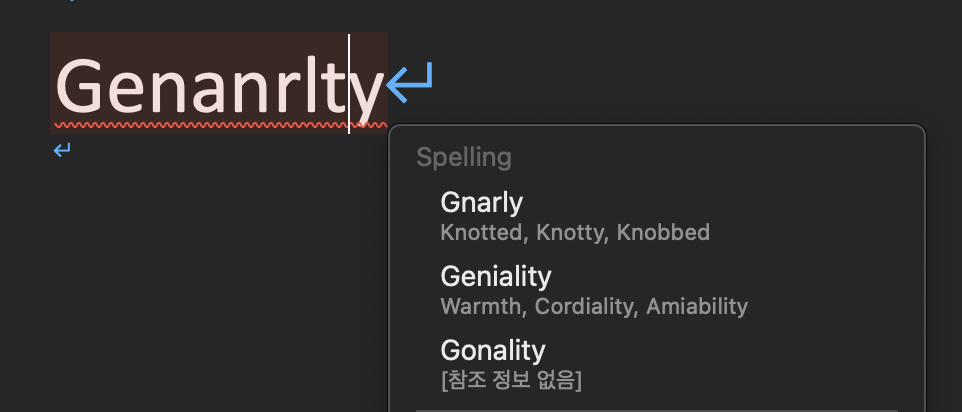
Edit distance는 두 string이 얼마나 가까운지 나타내는 척도입니다.
두 문자열 $S_1$ 과 $S_2$ 간의 edit distance는 $S_1$ 에서 아래 3가지 종류의 연산을 최소한 몇 번 수행하여 $S_2$ 를 만들 수 있는가로 정의됩니다.
Insertion : $S_1$ 의 아무 위치에 문자 하나를 추가합니다.
MONDT -> MONEDT
Deletion : $S_1$ 의 아무 위치에서 문자 하나를 제거합니다.
MONEDT -> MOMED
Substitution : $S_1$ 의 문자 하나를 다른 문자로 바꿉니다.
MONED -> MOMEY
🧐 Edit Distance 구하기
$S_1$(SNOWY) 과 $S_2$(SUNNY) 의 edit distance를 다음과 같은 표(gap table)로 나타내 보도록 하겠습니다.
| $S_1$ | S | - | N | O | W | Y |
| $S_2$ | S | U | N | N | - | Y |
| Insertion | Substitution | Deletion |
이때 $S_1$ 과 $S_2$ 의 table에서 마지막 column을 제거한 table은,
이에 해당되는 $S_1$ 과 $S_2$의 prefix 간의 edit distance를 나타냅니다.
따라서 prefix간의 edit distance가 더 짧다면,
그것에 해당하는 table과 제거한 컬럼을 통해 더 짧은 edit distance를 얻을 수 있습니다.
즉 $S_1$ 과 $S_2$ 간의 edit distance는
$S_1$ 과 $S_2$ 의 prefix간의 edit distance에 의해 결정할 수 있습니다.
Edit(i, j)를 두 prefix $S_1$[1, ..., i] 와 $S_2$[1, ..., j] 간의 edit distance라 하고,
$S_1$[1, ..., i] 와 $S_2$[1, ..., j] 간의 table에서 마지막 column에서 일어난 연산에 따라 다음과 같은 recurrence relation을 생각해 볼 수 있습니다.
⭐️ Case 1 : 마지막 Column에서 Deletion이 일어난 경우
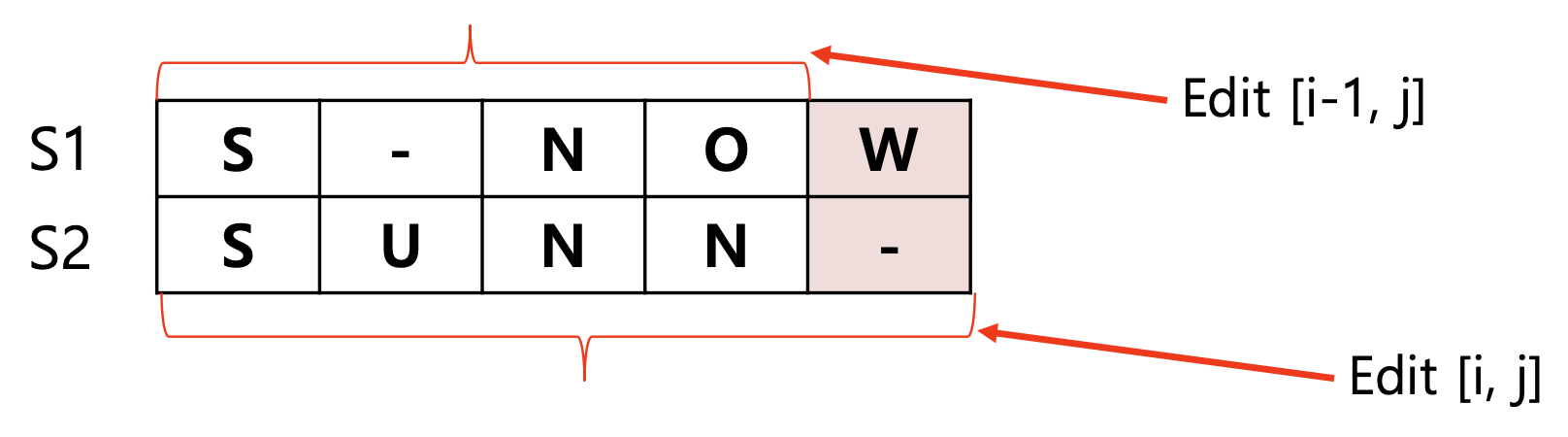
Edit(i, j) = Edit(i-1, j) + 1
⭐️ Case 2 : 마지막 Column에서 Insertion이 일어난 경우
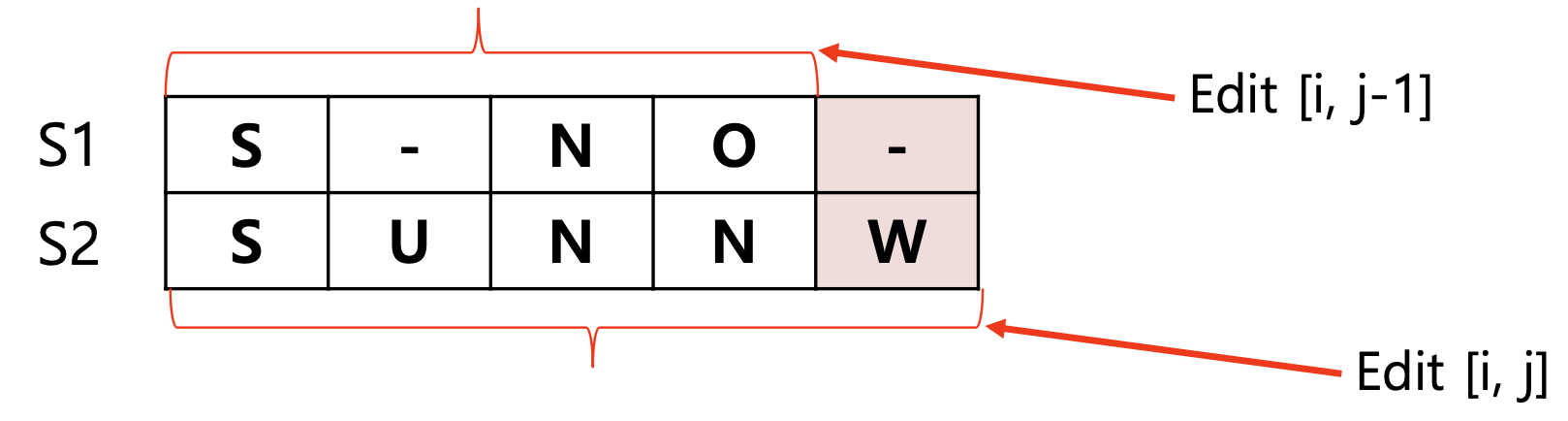
Edit(i, j) = Edit(i, j-1) + 1
⭐️ Case 3 : 마지막 Column에서 Substitution이 일어난 경우
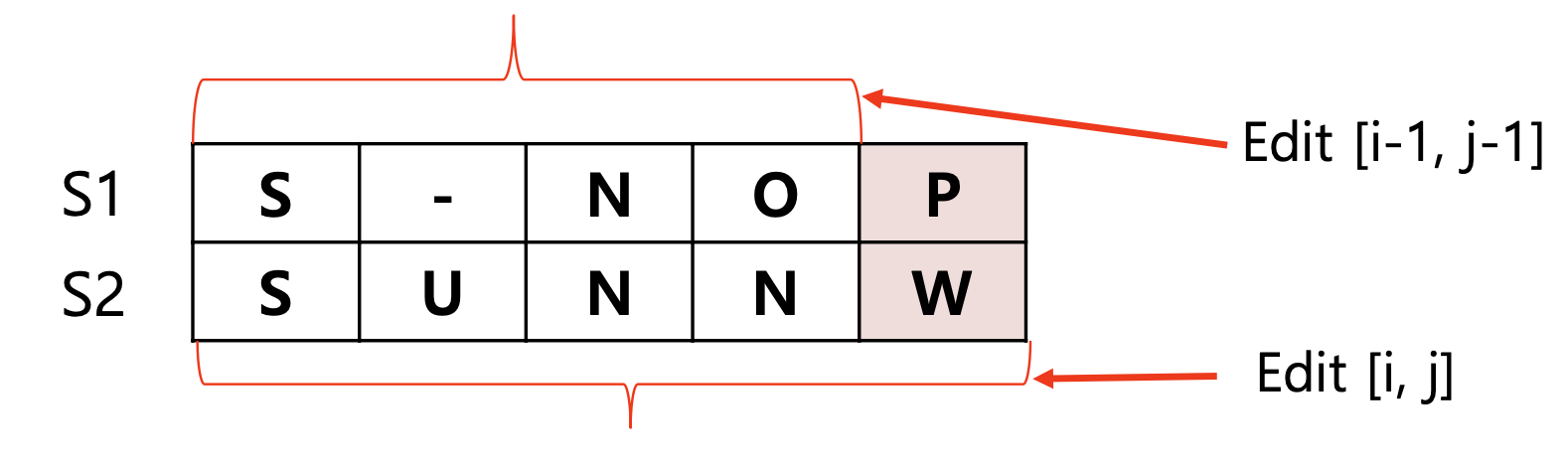
Edit(i, j) = Edit(i-1, j-1) + 1
이때 만약 Substitution이 발생하지 않고 두 문자가 같은 경우 즉, $S_1$[i] = $S_2$[j] 인 경우에는
Edit(i, j) = Edit(i-1, j-1) 입니다.
⭐️ Base Case
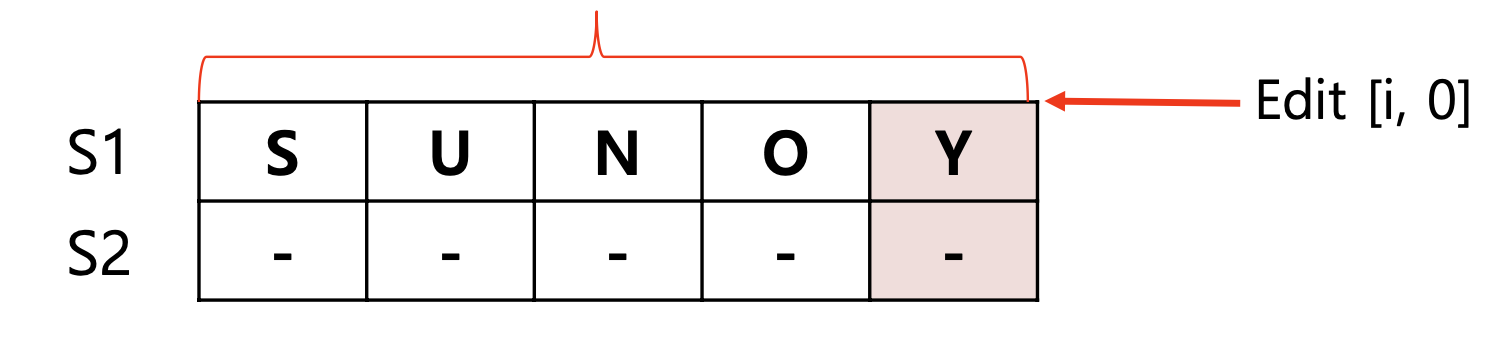
Edit(i, 0) = Edit(0, i) = i
위 사실들을 바탕으로 $Edit(i, j)$ 를 구하는 recurrence relation을 세우면 다음과 같습니다.
🧐 Recurrence relation
Case 1, 2, 3 중 가장 edit distance가 작은 것을 선택하는 relation입니다.
$$Edit(i, j) = \left\{\begin{matrix}
i & \;if \; j = 0 \\
j & \;if \; i = 0 \\
min\begin{Bmatrix}
Edit(i, j-1) + 1 \\
Edit(i-1, j) + 1 \\
Edit(i-1, j-1) + [A[i] \neq B[j]] \\
\end{Bmatrix} & \; otherwise\\
\end{matrix}\right.$$
🧐 예시
row를 먼저 채워가도 되고(row-major),
column을 먼저 채워나가도(column-major) 상관없지만,
row-major 방식으로 예제를 진행하도록 하겠습니다.
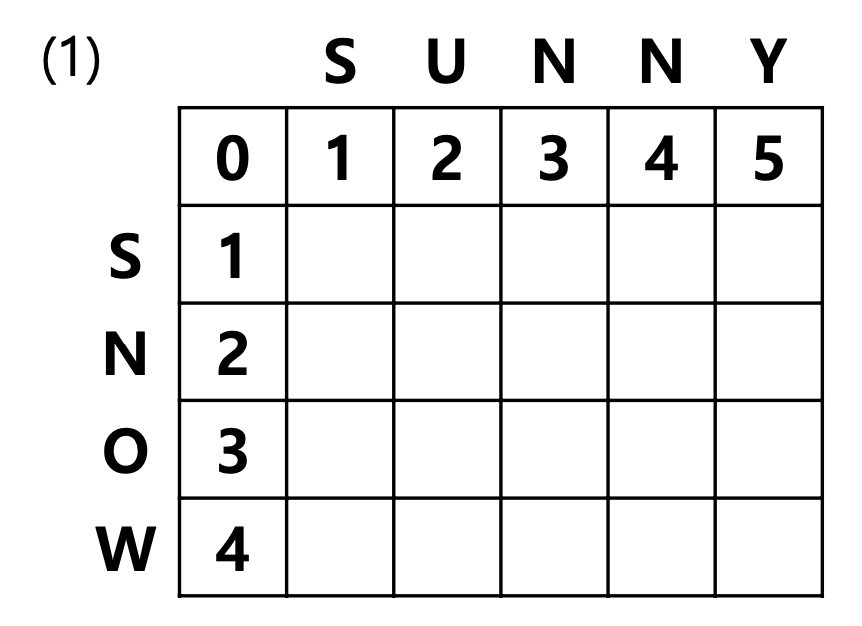
예시로 사용할 두 문자열은 $S_1 =$ SUNNY와 $S_2 =$ SNOW입니다.
최초 table은 다음과 같습니다.
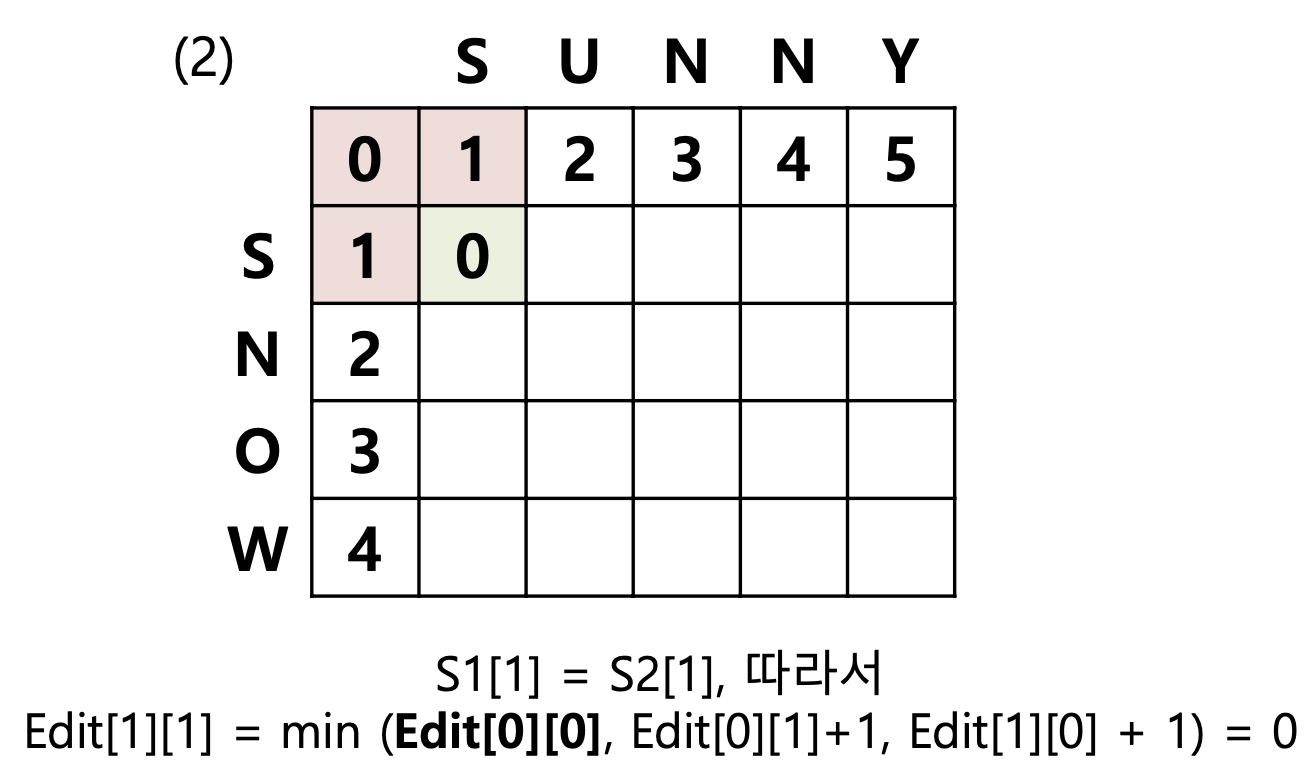
$S_1[1] = S_2[1]$ 이므로, 다음은 아래와 같습니다.(빨간색 3개를 비교)
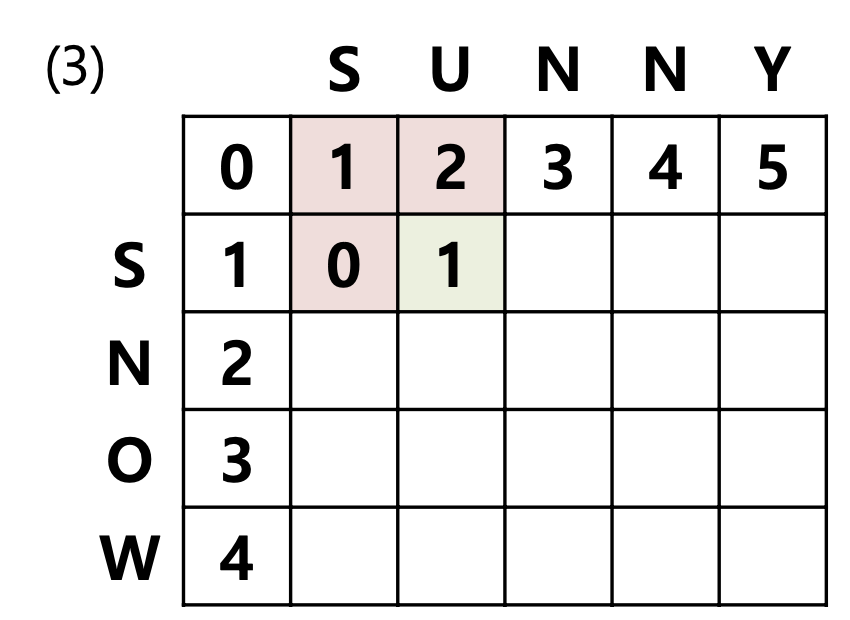
$S_1[1] \neq S_2[2]$ 이므로, 다음은 아래와 같습니다.(빨간색 3개를 비교)

$S_1[1] \neq S_2[3]$ 이므로, 다음은 아래와 같습니다.(빨간색 3개를 비교)
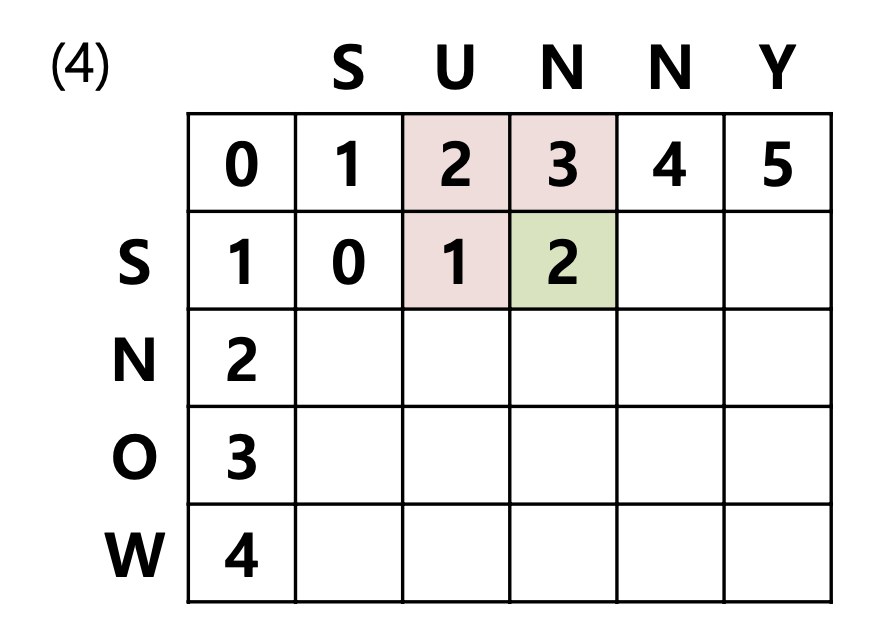

이런 식으로 왼쪽, 대각선 위쪽, 위쪽의 3가지 방향의 값들과 비교해가며 값을 채워나가면 다음과 같이 표를 완성시킬 수 있습니다.
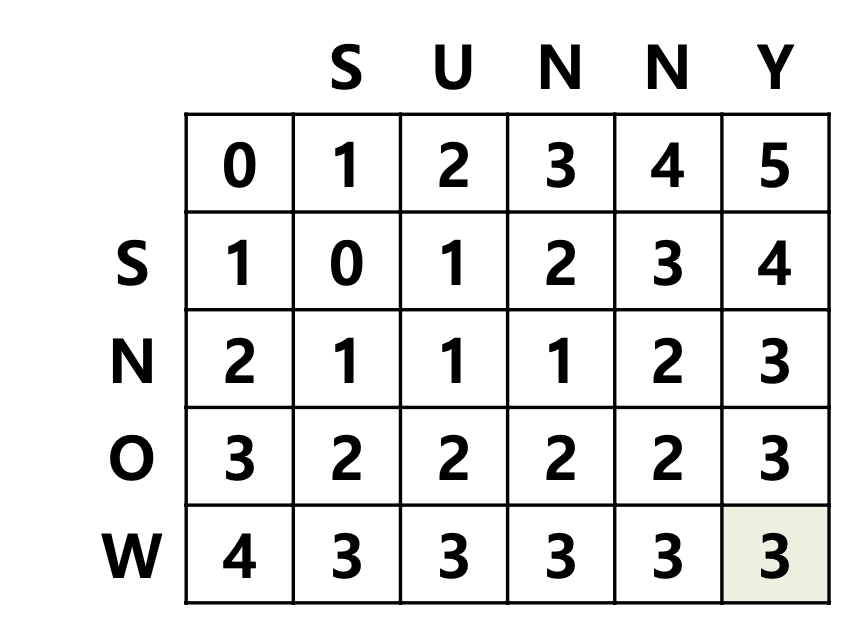
따라서 SUNNY와 SNOW 사이의 Edit distance는 3입니다.
🧐 Pseudocode

🧐 시간 복잡도
Edit Array의 요소 하나를 구할 때마다 $O(1)$ 의 시간이 소요되며,
Array는 두 문자열의 길이를 row와 column으로 하는 2차원 배열이므로
총 $O(n^2)$ 의 시간이 걸립니다.
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] DP(4) - 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2022.11.13 |
|---|---|
| [알고리즘] DP (3) - 벨만포드(Bellman-Ford) 알고리즘 (0) | 2022.11.12 |
| [알고리즘] DP (1) - LIS(최장 증가 부분 수열) (0) | 2022.11.10 |
| [알고리즘] DP (0) - DP 문제를 해결하는 방법 (0) | 2022.11.09 |
| [알고리즘] 그리디 (3) - Huffman Encoding(허프만 부호화) (0) | 2022.10.21 |