🧐 Reduction
어떠한 문제 X와 Y를 가정하도록 하겠습니다.
(엄밀한 정의는 아닙니다)
이 때 Y를 해결하는 어떠한 알고리즘이 존재하고, 해당 알고리즘을 이용하여 문제 X를 해결하는 알고리즘을 디자인 할 수 있는 경우, 문제 X에서 Y로의 Reduction이 가능하다고 합니다. (X is reducible to Y)
이를 보통 X $\leq$ Y 로 표현합니다.
즉 X $\leq$ Y 인 경우, X를 해결하는 것은 Y를 해결하는 것보다 절대로 어려울 수 없습니다.
다른 말로는 Y를 해결하는 것은 적어도 X를 해결하는 것 만큼 어렵다고 할 수 있습니다.
Reduction은 특정 문제를 해결하는 알고리즘을 디자인하거나,
어떤 문제를 해결하는 알고리즘이 존재하지 않는(혹은 매우 해결하기 힘든) 것을 증명하는데 사용됩니다.
🧐 예시 1 : Selection과 Sorting
문제의 Input은 다음과 같습니다.
Input : 길이가 n인 배열 A[1, ..., n]
Selection 문제와 Sorting 문제는 다음과 같이 정의됩니다.
Selection : A에서 k번째로 작은 element 찾기
Sorting : A를 non-decreasing order로 Sorting
이때 Sorting 문제를 해결하는 알고리즘이 존재하는 경우, Selection 문제는 A를 Sorting한 뒤, A[k]를 return하는 것으로 해결할 수 있습니다.
따라서 Selection에서 Sorting으로의 Reduction이 존재합니다.
🧐 예시 2 : Longest Increasing Subsequence 와 Longest Path in DAG
만약 DAG에서 longest path를 구하는 알고리즘이 존재한다고 하겠습니다.
이 경우 LIS의 Sequence를 DAG으로 변환한 뒤, 해당 DAG에서 longest path를 찾을 수 있습니다.
찾은 path를 구성하는 node들은 LIS의 element에 대응하게 됩니다.
따라서 LIS는 Longest path in DAG 문제로 reduction이 가능합니다.
🧐 문제의 종류(Types of Problems)
조금 뜬금없지만, 잠시 문제의 종류에 대해 살펴보도록 하겠습니다.
문제의 종류는 크게 Decision(결정), Search(탐색), Optimization(최적화)으로 나눌 수 있습니다.
👉 Decision Problem
답을 YES 또는 NO로 할 수 있는 문제를 의미합니다.
ex: A 에서 길이 3 이상의 increasing sequence가 존재하는가?
👉 Search Problem
ex: A 에서 길이 3 이상의 모든 element를 찾아라.
👉 Optimization Problem
ex: A 의 각 Substring이 increasing substring이 되도록 하는 A를 가장 적은 개수의 substring들로 partitioning하라.
🧐 Problem Instance
어떤 문제(problem)를 정의하는 input을 problem instance라고 합니다.
Problem과 Problem Instance는 같지 않습니다.
Problem은 특정 조건을 만족하는 Problem Instance들의 집합으로 정의할 수 있습니다.
Decision Problem X를 해결하는 알고리즘은, X에 속한 instance를 input으로 받은 뒤 YES/NO 중 하나의 대답을 출력합니다.
예를 들어 `Sequence A에서 길이 k 이상의 LIS가 존재하는가?`라는 결정 문제의 각 Instance는 Sequence A와 k입니다.
🧐 Decision Problem에 대한 Reduction
두 Decision Problem X, Y에 대하여 다음과 같은 관계가 존재하는 경우, X는 Y로 reducible 합니다.
(즉 Y를 풀면 X를 풀 수 있습니다)
1. X의 instance $I_X$ 를 받아 다음을 만족하는Y의 instance $I_Y$ 로 변환 가능해야 합니다.
2. Instance $I_Y$ 에 대한 Y의 답을 이용하여 instance $I_X$ 에 대한 X의 답을 구할 수 있습니다.
(Decision Problem에 한하여 두 답은 언제나 동일, 즉 Y에서 대답이 YES였으면 X에서도 YES여야 합니다.)
X는 Y로 reducible 한 경우, X의 instance를 Y의 instance로 바꾸는 알고리즘을 X에서 Y로의 reduction이라고 합니다.
이제 두 decision problem X에서 Y로의 reduction R이 주어지고, 문제 Y를 해결하는 알고리즘 $A_Y$ 가 주어지는 경우, 문제 X를 해결하는 알고리즘 $A_X$ 를 다음과 같이 디자인 할 수 있습니다.

이때 R과 $A_Y$가 Polynomial time (다항 시간) 알고리즘이라면, $A_X$ 또한 Polynomial time 알고리즘이 됩니다.
🧐 Polynomial Time Reductions
어떤 알고리즘이 polynomial time에 동작하는 경우, 즉 O( poly( |instance size| )인 경우 해당 알고리즘을 보통 efficient algorithm이라고 합니다.
어떤 문제를 해결하는 efficient algorithm을 찾기 위해서는 보통 polynomial time에 동작하는 reduction만을 생각하게 되며, 이를 polynomial-time reduction이라고 합니다.
문제 X에서 Y로의 polynomial time reduction이 존재하는 경우, 이를 X $\leq_p$ Y로 표기하며,
X $\leq_p$ Y이고 Y를 해결하는 polynomial time algorithm $A_Y$ 가 존재한다면,
문제 X를 해결하는 polynomial time algorithm $A_X$ 또한 존재합니다.
🧐 Independent Set
그래프 G = (V, E)에 대하여 Independent Set을 다음과 같이 정의합니다.
정점들의 집합 V' (V' $\subset$ V)에 속한 모든 정점들이 서로 adjacent 하지 않으면 V'는 G의 independent set입니다.
🧐 Clique
그래프 G = (V, E)에 대하여 Clique를 다음과 같이 정의합니다.
정점들의 집합 V'(V' $\subset$ V)에 속한 모든 정점들이 서로 adjacent 하다면 V'는 G의 clique 입니다.
예를 들어 다음과 같습니다.

🧐 Independent Set과 Clique 사이의 Reduction
우선 Independent Set과 Clique Problem을 각각 다음과 같이 정의하겠습니다.
👉 Independent Set Problem
Instance : 그래프 G, 음수가 아닌 정수 k
Goal : G가 크기 k 이상인 independent set을 가지고 있는지 판별
👉 Clique Problem
Instance : 그래프 G, 음수가 아닌 정수 k
Goal : G가 크기 k 이상인 clique을 가지고 있는지 판별
위와 같은 Problem들에 대하여 Independent Set $\leq_p$ Clique 가 성립합니다.
👉증명
Independent set의 instance (G, k)를 Clique의 instance (G', k)로 변환하겠습니다.
이때 G'은 G와 정점들은 모두 동일하지만, G에서 간선이 존재하지 않는 모든 두 정점 사이에만 간선이 존재하는 그래프라 하겠습니다.
이때 G'에 간선 (u, v)가 존재한다는 것은 G에서는 간선이 없는, 즉 adjacent하지 않다는 것을 의미합니다.
V가 G에서 size k의 independent Set인 경우, V는 G'에서 size k인 Clique입니다.
이에 대한 증명은 다음과 같습니다.
(1) V가 G의 Independent Set이라고 하겠습니다.
그러면 V의 임의의 두 정점 u, v에 대하여, G에서 edge(u, v)는 존재하지 않습니다.
따라서 G'의 정의에 의해 G'에서는 edge(u, v)가 존재해야 하고, 따라서 이들은 adjacent 합니다.
이는 V의 모든 정점들에 대하여 성립하므로, G'에서 V에 속한 임의의 두 정점들은 반드시 adjacent 합니다.
따라서 이들은 G'의 Clique입니다.
(2) V가 G'의 Clique라고 하겠습니다.
그러면 V의 임의의 두 정점 u, v에 대하여, G'에서 edge(u, v)는 존재합니다.
G'에 edge(u, v)가 존재한다는 것은, G'의 정의에 의해 G에는 edge(u, v)가 존재하지 않는다는 것을 의미합니다.
이는 V의 모든 정점들에 대해서 성립하므로, G에서 V에 속한 임의의 두 정점들은 반드시 adjacent 하지 않습니다.
따라서 이들은 G의 independent set입니다.
이를 통해 Independent set의 instance가 YES인 경우에만(iff) Clique의 instance가 YES를 반환함을 증명하였습니다.
또한 G와 정점들은 모두 동일하지만, G에서 간선이 존재하지 않는 모든 두 정점 사이에만 간선이 존재하는 그래프를 construct 하는 것이 polynomial time에 가능하므로, Independent Set $\leq_p$ Clique 가 성립합니다.
🧐 Vertex Cover
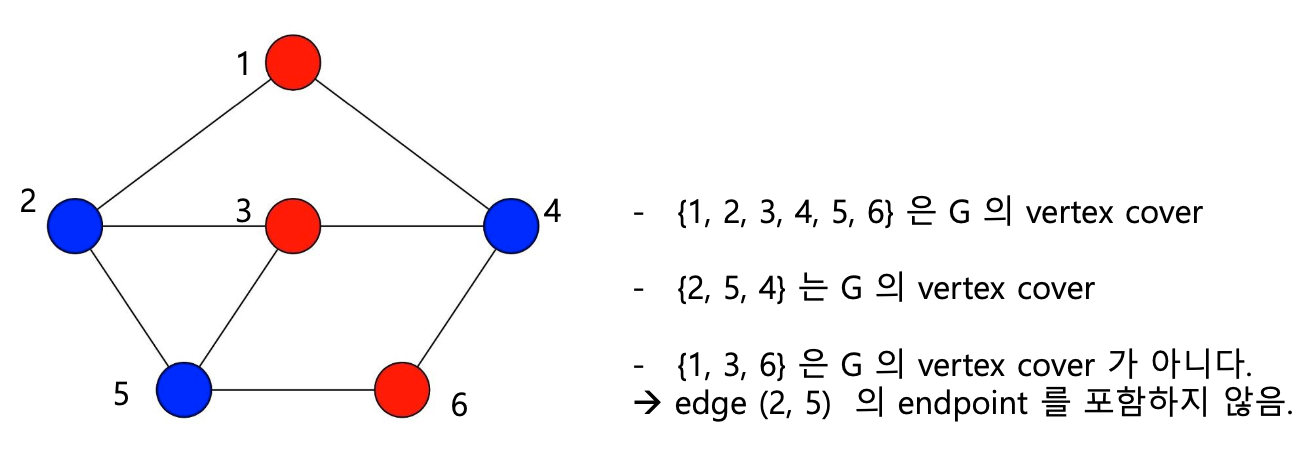
그래프 G = (V, E)에 대하여 Vertex Cover를 다음과 같이 정의합니다.
G의 모든 edge들의 endpoint를 적어도 하나 이상 포함하는 vertex set S (S $\subset$ V)를 G의 Vertex Cover라고 합니다.
🧐 Independent Set과 Vertex Cover 사이의 Reduction
Independent Set Problem의 정의는 위와 동일하며, Vertex Cover Problem을 아래와 같이 정의하겠습니다.
👉 Vertex Cover Problem
Instance : 그래프 G, 음수가 아닌 정수 k
Goal : G가 크기 k 이하인 Vertex Cover를 가지고 있는지 판별
위와 같은 Problem들에 대하여 Independent Set $\leq_p$ Vertex Cover 가 성립합니다.
👉증명
(1) S가 G의 independent set이라 하겠습니다.
임의의 G의 edge(u, v) $\in$ E 에 대해서도 u $\notin$ S 이거나 v $\notin$ S 입니다. (둘 다 S에 속하지 않을 수도 있습니다.)
따라서 u $\in$ (V \ S) 이거나 v $\in$ (V \ S) 이여야 합니다. (둘 다 속할수도 있습니다)
따라서 (V \ S)는 G의 Vertex Cover가 됩니다.
(2) V \ S가 G의 Vertex Cover라는 가정에서부터 시작하겠습니다.
이 경우 S에 속하는 임의의 두 정점 v, u에 대하여, (u, v)는 edge가 될 수 없습니다.
(만약 edge가 된다면 V \ S가 이들을 커버하지 못하므로 모순입니다.)
따라서 S는 G의 independent set입니다.
이를 통해 `정점이 n개인 그래프 G가 크기 k 이상의 independent set을 가지고 있다`는 것은,
`G가 크기 n-k 이하의 vertex cover를 가지고 있다`와 동치라는 것을 알 수 있습니다.
따라서 Independent Set Problem의 instance (G, k)에 대한 답과 Vertex Cover Problem의 instance(G, n-k)는 동일한 답을 출력합니다.
Instance (G, k)가 주어지면 (G, n-k)는 O(1) 시간에 construction이 가능하므로, (Independent Set) $\leq_p$ (Vertex Cover) 라는 것을 증명할 수 있습니다.
그러므로 independent set을 해결하는 efficient algorithm이 존재하지 않는다면, vertex cover를 해결하는 efficient algorithm 또한 존재하지 않습니다.
🧐 Propositional Formulas
Boolean variable들의 집합 {$x_1$, $x_2$, ..., $x_n$}에 대하여, Literal, Clause, Conjunctive normal form(CNF) formula를 각각 다음과 같이 정의합니다.
Literal (리터럴) : Boolean variable $x_i$ 혹은 그 부정(negation) $\neg x_i$ 를 의미합니다.
Clause (절) : literal들의 disjunction(논리 합)을 의미합니다. (ex: $x_1 \vee x_2 \vee \neg x_3$)
Conjunctive normal form (CNF) formula : clause 들의 conjunction(논리 곱)으로 표현된 proportional formula(명제 식)을 의미합니다.
CNF formula의 예시로는 ($x_1 \; \vee \;x_2\; \vee\; \neg x_4$) $\wedge$ ($x_2 \vee \neg x_3$) $\wedge$ $x_5$
CNF formula F의 각 clause가 정확히 k개의 literal로 구성되어 있다면, F는 k-CNF formula라고 합니다.
🧐 SAT- problem
CNF formula F가 주어졌을 때,
F의 값이 true가 되도록 F의 각 variable에 true/false를 할당(Assign)할 수 있는지 판별하는 문제를 의미합니다
이때 할당할 수 있는 경우 F는 satisfiable 하다고 합니다.
예를 들어 다음과 같습니다.

3-CNF formula에 대한 SAT problem을 3-SAT 이라고 합니다.
🧐 Independent Set과 3-SAT 사이의 Reduction
Instance : 3-CNF formular F
Goal : 다음 성질을 만족하면서 F의 size에 대한 polynormial time 안에 그래프 $G_F$와, 음수가 아닌 정수 k를 counstruct 하는 알고리즘을 디자인하기
성질 : $G_F$ 가 크기 k의 independent set을 가지고 있는 경우에만 (if and only if) F는 satisfiable하다.
이를 해결하기 위해 3-SAT의 중요한 성질들에 대해 알아보도록 하겠습니다.
1. F 가 true가 되게 하는 variable assignment를 찾는다는 것은, F의 variable 들에 해당하는 값들을 할당하면, F의 각 clause가 모두 true가 된다는 것을 의미합니다.
2. 각 clause에서 적어도 하나의 literal만 true이면 F는 무조건 true가 됩니다.
따라서 F의 각 clause에서 literal 하나씩을 골라 그들을 모두 true가 되게 하는 assignment가 존재하는지 여부를 확인하면 됩니다.
3. $x_i$와 $\neg x_i$ 는 같이 선택(true로 할당)할 수 없으며, 이와 같이 선택한 경우 confiliction(충돌)이 일어났다고 합니다.
이제 3-SAT problem에서 Independent Set problem으로의 reduction을 생각해 보도록 하겠습니다.
F의 각 literal에 대하여, 이에 대응하는 $G_F$의 유일한 정점이 존재합니다.
(이때 같은 literal에 대해서는 표기는 같으나 다르게 취급되는 정점으로 대응시킵니다.)
F의 각 clause를 구성하는 3개의 literal들은 $G_F$ 에서 서로 triangle을 이룹니다.
따라서 $G_F$ 의 independent set은 각 clause의 literal들에 대응하는 vertex 3개 중 최대 한 개만을 포함하게 됩니다.
$x_i$ 와 $\neg x_i$ 가 존재한다면 $G_F$ 에서 이 둘을 edge로 이어줍니다.
따라서 G의 independent set에 대응하는 literal들은 confliction이 발생하지 않습니다.
k는 F를 구성하는 clause의 총 개수로 둡니다.
예시는 다음과 같습니다.

위와 같은 Problem들에 대하여 3-SAT $\leq_p$ Independent Set이 성립합니다.
👉증명
(1) S가 크기 k인 $G_F$ 의 independent set이라 하겠습니다.
S는 각 cluase에 대응하는 3개의 정점들 중 정확히 하나를 포함해야 합니다.
(k는 clause의 개수와 같으므로, 만약 하나라도 포함되지 않는 clause가 있다면, 어느 하나의 cluase에 대응되는 두 개의 정점이 S에 포함됩니다. 이때 해당 두 정점은 adjacent 하므로 S가 independent set이라는 가정에 모순됩니다.)
S는 confliction 관계에 있는 두 literal에 해당하는 vertex 두 개를 모두 포함할 수 없습니다.
(이 둘은 adjacent하기 때문입니다.)
따라서 S에 속한 정점들에 대응하는 literal들이 true가 되도록, F의 variable 들에 할당하면 ,F를 구성하는 모든 clause 들은 true가 되며, 따라서 F는 true가 됩니다.
(2) F가 satisfiable이 되는 assignment가 존재한다고 하겠습니다.
이 경우 해당 assignment에서 F의 각 clause마다 true값을 갖는 literal을 하나씩 고르면, 해당 literal에 해당하는 vertex들은 $G_F$의 independent set이 됩니다.
Clause가 총 k개 있으므로, 이 경우 GF는 크기가 k인 independent set을 가지게 됩니다.
3-SAT에 대응되는 그래프를 construct 하는 것은 polynomial time내에 가능하며,
따라서 3-SAT 문제의 instance $I_X$ 에서 Independent Set 문제의 instance $I_Y$ 로의 polynomial time reduction이 존재합니다.
또한 위에서 살펴본 것과 같이, $I_X$ 가 X에 대해 YES를 반환하는 instance인 경우에만, $I_Y$ 가 문제 Y에 대해 YES를 출력하는 instance이므로, 3-SAT $\leq_p$ Independent Set이 성립합니다
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] NP-Complete와 NP-Hard (0) | 2022.12.06 |
|---|---|
| [알고리즘] P와 NP (1) | 2022.12.06 |
| [알고리즘] Counting Sort (계수 정렬) (0) | 2022.12.05 |
| [알고리즘] Adversary Argument (2) | 2022.12.05 |
| [알고리즘] DP(4) - 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2022.11.13 |