🧐 플로이드 와샬 알고리즘
플로이드 와샬 알고리즘은 음의 사이클이 없는 그래프 상에 존재하는 모든 정점에 대하여,
각 정점 간의 최단거리를 구할 수 있는 알고리즘으로,
기본 아이디어는 거쳐가는 정점을 기준으로 최단 거리를 구하는 것입니다.
V = { 1, 2, ..., n } 으로 두고, G의 임의의 두 정점 i, j에 대하여 dist(i, j, k)를 다음과 같이 정의합니다.
정점 (1, 2, ..., k) 만을 path의 중간 정점(intermediate vertex)으로 포함시킬 수 있을 때, i 에서 j로의 최단 경로의 길이
🧐 Recurrence Relation
Base Case( k = 0 )
dist (i, j, 0) = 0 : i = j 인 경우
dist (i, j, 0) = w(i, j) : 간선(i, j)가 존재하는 경우
dist (i, j, 0) = '무한대' : 간선(i, j)가 존재하지 않는 경우
Inductive Step
dist (i, j, k) 의 길이를 가진 path를 두 가지 case로 나누어 보면,
Case 1 : 정점 k를 지나치지 않는 경우, 즉 정점 k를 중간 거점으로 사용 가능하더라도 (1, ..., k-1)을 중간 거점으로 사용했을 때와 비교해서 최단경로가 줄어들지 않을 때
이 경우 dist(i, j, k) =dist(i, j, k-1)
Case 2 : 정점 k를 지나가는 경우, 즉 정점 k를 중간 거점으로 사용 가능하면, (1, ..., k-1)을 중간 거점으로 사용했을 때와 비교해서 최단경로가 줄어들 때
이 경우 dist(i, j, k) = dist(i, k, k-1) + dist(k, j, k-1)
Case 2 의 경우 중간 지점으로 k를 거친다면, i에서 k로의 path와 k에서 j로의 path는 중간 지점으로 k를 포함해서는 안됩니다.
만약 중간 지점으로 k를 포함한다면 k를 두 번 거치게 되고, 이것이 최단경로가 되는 경우 이는 negative cycle이 포함된 것이기 때문입니다. (k -> ... -> k 를 했을 때 비용이 줄어들기 때문)
즉 따라서 다음과 같은 Recurrence Relation이 도출됩니다.
dist(i, j, k) = min( ( dist(i, k, k-1) + dist(k, j, k-1)) , dist(i, j, k-1) )
🧐 플로이드 와샬 알고리즘
플로이드 와샬 알고리즘은 반복문의 중심을 거쳐가는 정점으로 설정합니다.
즉 첫번째 반복에서는 1번 정점을 거쳐가는 경로를, n번째 반복에서는 n번 정점을 거쳐가는 경로를 확인합니다.
1. 총 n번의 반복이 진행되며, k 번째 반복이 끝날 때마다 G의 모든 정점 i, j에 대하여 dist(i, j, k)가 dist(i, j)에 저장됩니다.
2. 시작할 때에는 앞선 base case에 맞게 dist 값을 정해줍니다.
3. 이후 k번째 반복마다 모든 정점 i, j 에 대하여 다음 작업을 반복합니다.
dist(i, k, k-1) + dist(k, j, k-1) < dist(i, j, k-1) 인 경우, 즉 k를 거쳐가면 최단 경로가 줄어드는 경우,
dist(i, j)를 dist(i, k, k-1) + dist(k, j, k-1)로 업데이트합니다.
(업데이트가 되지 않는 경우에는 k번째 반복이 끝나면 dist(i, j, k)가 자동으로 dist(i, j, k-1)이 됩니다.)
🧐 예시
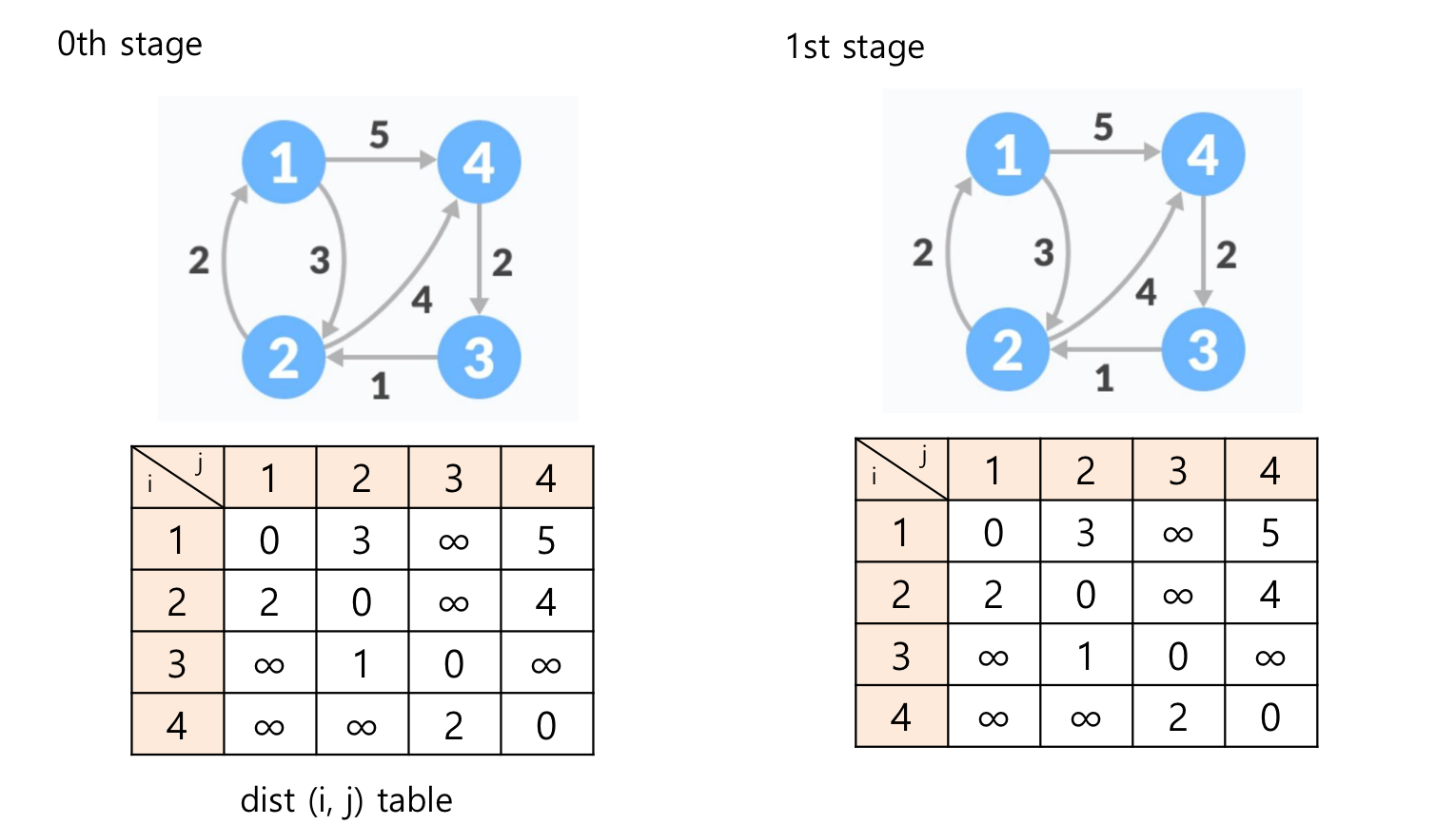
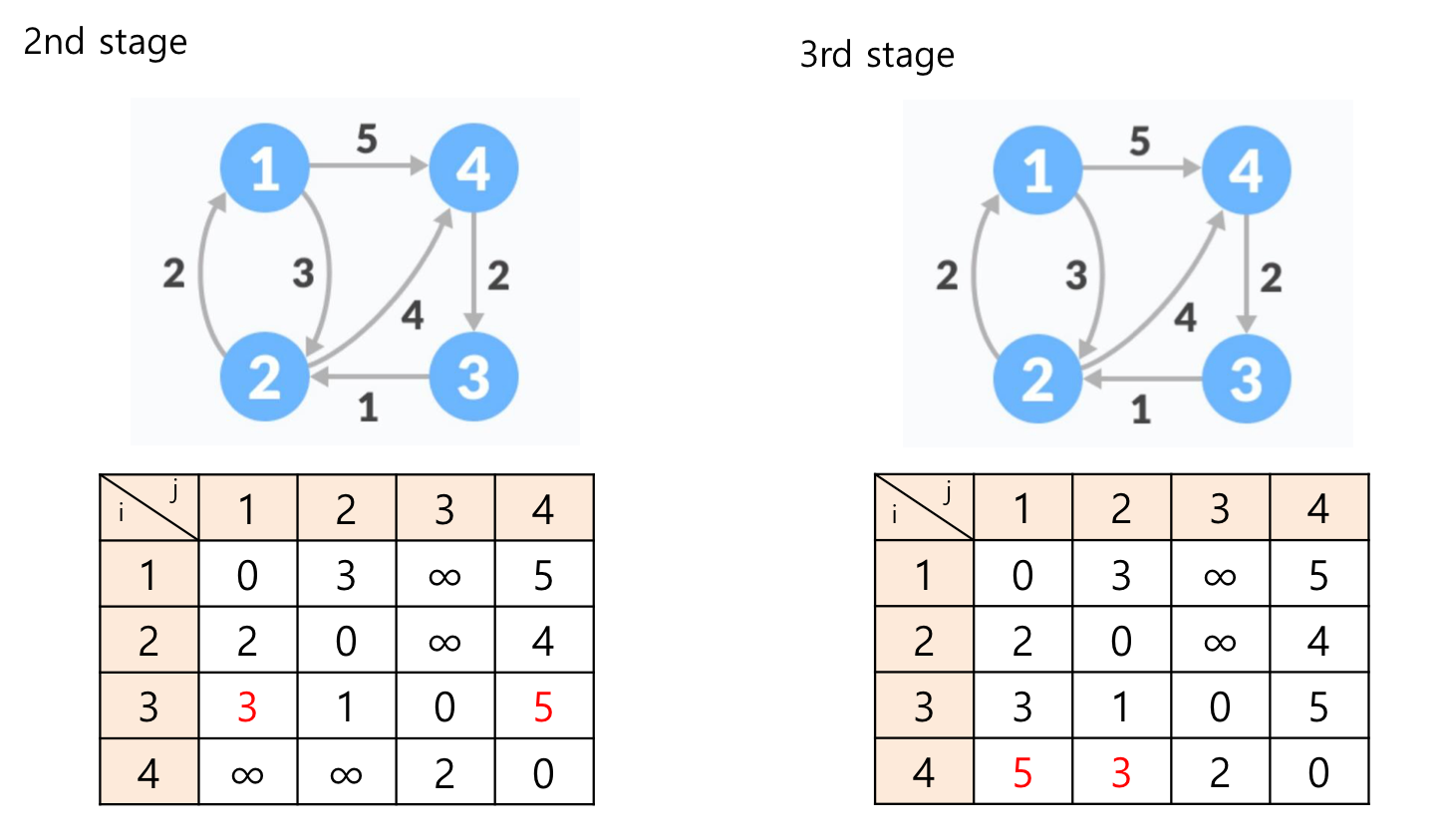
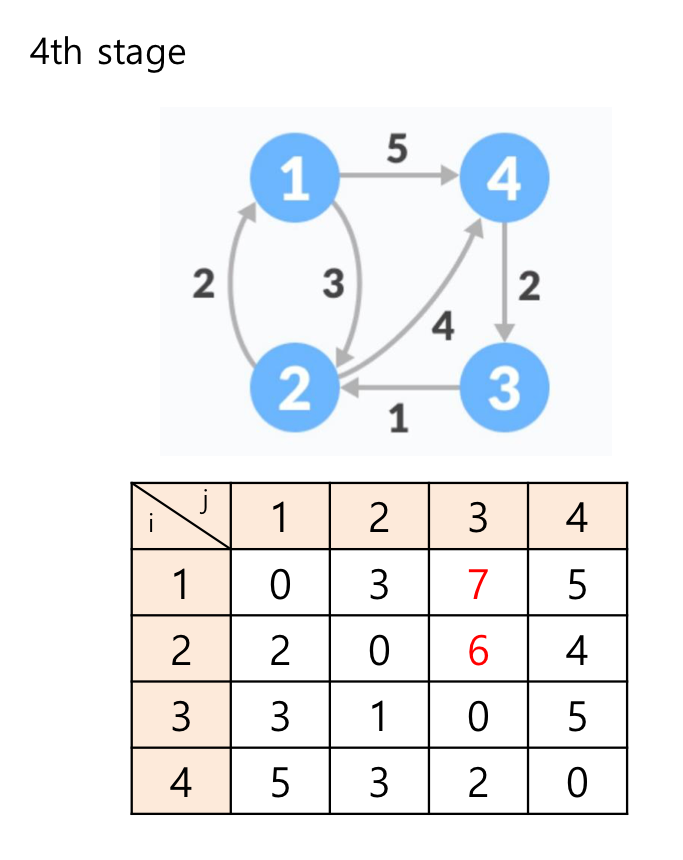
2번째 스테이지의 경우, 중간 정점은 2입니다.
(3 -> 1) 경로를 확인해 보면, 기존 값보다 (3 -> 2) + (2 -> 1) = 1 + 2 = 3 입니다.
즉 2번째 스테이지에서 3 -> 1 경로가 업데이트 되며, 나머지도 비슷하게 진행됩니다.
🧐 수도코드

🧐 시간 복잡도
총 n+1번 반복하며 : $O(n)$
각 반복마다 모든 i, j 에 대해서 dist(i, j)를 업데이트 : $O(n^2)$
따라서 $O(n^3)$
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] Counting Sort (계수 정렬) (0) | 2022.12.05 |
|---|---|
| [알고리즘] Adversary Argument (2) | 2022.12.05 |
| [알고리즘] DP (3) - 벨만포드(Bellman-Ford) 알고리즘 (0) | 2022.11.12 |
| [알고리즘] DP (2) - Edit Distance(편집 거리) (0) | 2022.11.12 |
| [알고리즘] DP (1) - LIS(최장 증가 부분 수열) (0) | 2022.11.10 |