정규분포 (Normal Distribution)
정규분포는 연속 확률 분포에 속하며 아래와 같이 정의됩니다.
확률변수 X가 다음 p.d.f를 갖는 연속 분포를 갖는 경우, 평균(mean) μ 와 분산(variance) σ^2을 가지는 정규분포를 따릅니다.
$$p.d.f\;\;\; f(\;x\;|\; \mu,\; \sigma^{2}) \;= \;\;\;\;\frac{1}{\sqrt{2\pi}\sigma} \cdot exp(-\frac{(x-\mu)^{2}}{2\sigma^{2}})\;\;\;\;\;\;\;for\; -\infty < x < \infty $$
그리고 정규분포는 다음과 같습니다.
$$X \sim N(\mu, \sigma^{2})$$
(이때 평균 μ는 bounded(-∞< μ <∞)이고, 분산은 σ^2 >0 입니다.)
정규분포의 적률생성함수(m.g.f)
다음과 같은 정규분포를 가지는 확률변수 X에 대하여,
$$X \;\sim N(\mu, \sigma^{2})$$
X에 대한 m.g.f는 다음과 같습니다.
$$\psi(t) = exp(\; \mu t + \frac{1}{2}\sigma^{2}t^{2})$$
증명)
우선 정규분포의 정의에 의해, 정규분포의 p.d.f는 다음과 같습니다.
$$f \;: \;\;\frac{1}{\sqrt{2\pi}\sigma} \cdot exp(-\frac{(x-\mu)^{2}}{2\sigma^{2}})$$
m.g.f의 정의에 따라, 정규분포의 적률생성함수는 다음과 같이 구할 수 있습니다.
$$\psi(t) = E(e^{tx}) = \int^{\infty}_{-\infty}e^{tx}f(x)\;dx$$
$$= \int^{\infty}_{-\infty} e^{tx} \cdot \frac{1}{\sqrt{2\pi}\sigma} \cdot exp(-\frac{(x-\mu)^{2}}{2\sigma^{2}})\;dx$$
$$= \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma} \cdot exp(tx-\frac{(x-\mu)^{2}}{2\sigma^{2}})\;dx$$
이때, 자연상수 e의 지수에 대한 식을 변형해 보도록 하겠습니다.
$$tx-\frac{(x-\mu)^{2}}{2\sigma^{2}}$$
$$ = \frac{2\sigma^{2}tx}{2\sigma^{2}}-\frac{(x-\mu)^{2}}{2\sigma^{2}}$$
$$= \frac{2\sigma^{2}tx}{2\sigma^{2}}- \frac{(x-\mu)^{2} - 2(x-\mu)\sigma^{2}t + (\sigma^{2}t)^{2} \;\;-\;\;( \;- 2(x-\mu)\sigma^{2}t + (\sigma^{2}t)^{2} )}{2\sigma^{2}}$$
$$= \frac{2\sigma^{2}tx}{2\sigma^{2}}- \frac{(x-\mu)^{2} - 2(x-\mu)\sigma^{2}t + (\sigma^{2}t)^{2} }{2\sigma^{2}}\;-\;\frac{ 2(x-\mu)\sigma^{2}t - (\sigma^{2}t)^{2} }{2\sigma^{2}}$$
이때 양쪽 끝 항을 묶어주고, 가운데 항을 완전제곱식으로 변형하면
$$= \frac{2\sigma^{2}tx - 2(x-\mu)\sigma^{2}t + (\sigma^{2}t)^{2} }{2\sigma^{2}}- \frac{(x-\mu-\sigma^{2}t)^{2} }{2\sigma^{2}}$$
위 식을 전개하면
$$= \frac{2\sigma^{2}tx - 2x\sigma^{2}t + 2\mu\sigma^{2}t + (\sigma^{2}t)^{2} }{2\sigma^{2}}- \frac{(x-\mu-\sigma^{2}t)^{2} }{2\sigma^{2}}$$
$$= \frac{2\mu\sigma^{2}t + (\sigma^{2}t)^{2} }{2\sigma^{2}}- \frac{(x-\mu-\sigma^{2}t)^{2} }{2\sigma^{2}}\;\;\;\; \because \;\; 2\sigma^{2}tx = 2x\sigma^{2}t$$
$$= \frac{2\mu t + \sigma^{2}t^{2} }{2}- \frac{(x-\mu-\sigma^{2}t)^{2} }{2\sigma^{2}}$$
이렇게 해서 자연상수 e의 지수의 식을 변형하였습니다. 다시 이를 기존의 식에 대입하면,
$$= \int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma} \cdot exp(\frac{2\mu t + \sigma^{2}t^{2} }{2}- \frac{(x-\mu-\sigma^{2}t)^{2} }{2\sigma^{2}})\;dx$$
이때 e의 지수의 왼쪽 식은 x가 포함되지 않은, 즉 적분에서 상수로 취급되는 값이므로 밖으로 빼내어 다음과 같이 쓸 수 있습니다.
$$= exp(\frac{2\mu t + \sigma^{2}t^{2} }{2}) \cdot\int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma} \cdot exp(-\frac{(x-\mu-\sigma^{2}t)^{2} }{2\sigma^{2}})\;dx$$
$$= exp(\frac{2\mu t + \sigma^{2}t^{2} }{2}) \cdot\int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma} \cdot exp(-\frac{(x-(\mu+\sigma^{2}t))^{2} }{2\sigma^{2}})\;dx$$
이때 다음과 같이 치환하면
$$\mu+\sigma^{2}t = \mu'$$
$$= exp(\frac{2\mu t + \sigma^{2}t^{2} }{2}) \cdot\int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma} \cdot exp(-\frac{(x-\mu')^{2} }{2\sigma^{2}})\;dx$$
이때 적분되는 함수는 평균 μ', 분산 σ^2을 가지는 정규분포를 따르는 확률변수 X에 대한 c.d.f 이며,
확률밀도함수의 성질에 따라 이를 (-무한대, +무한대)까지 적분한 값은 1입니다.
따라서
$$exp(\frac{2\mu t + \sigma^{2}t^{2} }{2}) \cdot\int^{\infty}_{-\infty} \frac{1}{\sqrt{2\pi}\sigma} \cdot exp(-\frac{(x-\mu')^{2} }{2\sigma^{2}})\;dx$$
$$=exp(\frac{2\mu t + \sigma^{2}t^{2} }{2}) \cdot 1$$
$$=exp(\frac{2\mu t + \sigma^{2}t^{2} }{2})$$
$$= exp(\; \mu t + \frac{1}{2}\sigma^{2}t^{2})$$
정규분포의 평균과 분산
위의 확률변수 X에 대한 평균과 분산은 다음과 같습니다.
$$E(X) = \mu$$
$$Var(X) = \sigma^{2}$$
증명은 다음과 같습니다.
$$\psi'(t) = (\; \mu +\sigma^{2}t\; ) exp(\; \mu t + \frac{1}{2}\sigma^{2}t^{2}) $$
$$\psi''(t) = (\; [\mu + \sigma^{2}t]^{2}+ \sigma^{2} \;) exp(\; \mu t + \frac{1}{2}\sigma^{2}t^{2}) $$
$$E(X) = \psi'(0) = \mu$$
$$Var(X) = \psi''(0) - \psi'(0)^{2}= \sigma^{2}$$
정규분포의 형태
정규분포는 다음과 같은 형태를 가집니다.
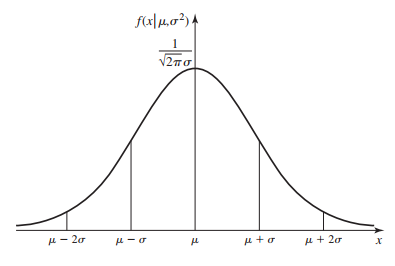
정규분포의 p.d.f는 다음과 같으며,
$$p.d.f: \;\; f(x| \mu, \sigma^{2}) = \frac{1}{\sqrt{2\pi}\sigma} \cdot exp(-\frac{1}{2} \cdot (\frac{X-\mu}{\sigma})^{2})$$
따라서 x의 값이 평균(µ)과 같을 때, 최댓값을 가집니다.
형태가 종과 닮았다 하여 bell curve 형태라 불리며, 중요한 점은 평균을 기준으로 대칭(Symmetric)이라는 점입니다.
또한 분산의 값이 커질수록 더욱 평평한(flat) graph가 됩니다.
선형 변환(Linear Transformation)
확률변수 X와 Y를 다음과 같이 정의하였을 때,
$$X \; \sim N(\mu, \sigma^{2})$$
$$ Y =aX + b$$
확률변수 Y도 정규분포를 따르며, 따르는 정규분포는 다음과 같습니다.
$$Y\; \sim N(a\mu + b , a^{2}\sigma^{2})$$
증명)
X와 Y에 대한 m.g.f를 다음과 같이 정의하겠습니다.
$$\psi_X,\;\; \psi_Y$$
이때 Y=aX + b 이므로, Y에 대한 m.g.f는 다음과 같습니다.(m.g.f를 배울 때 증명하였습니다.)
$$\psi_Y(t) = e^{tb} \psi(at)$$
$$= e^{tb} \; exp(\;\mu\; (at) + \frac{1}{2} \sigma^{2} (at)^{2})$$
$$= exp( t\;(\mu a + b) + \frac{1}{2} (\sigma a)^{2} t^{2})$$
마지막으로 유도된 식은 다음과 같이 쓸 수 있습니다.
$$ exp( t\mu' + \frac{1}{2} \sigma'^{2} t^{2}) \;\;\;\; \mu' = \mu a + b, \;\;\; \sigma' = a\sigma$$
따라서 다음과 같은 결론이 유도됩니다.
$$Y\; \sim N(a\mu + b , a^{2}\sigma^{2})$$
Standard Normal Distribution (SND, 표준 정규 분포)
SND는 평균이 0, 분산이 1인 정규분포로써, 다음과 같이 정의됩니다.
$$N(0, 1^{2})$$
또한 SND의 p.d.f와 c.d.f를 각각 다음과 같은 기호로 표시합니다.
$$\phi, \Phi$$
SND의 p.d.f는 다음과 같습니다.
$$ \phi(x) = f(x | 0, 1^{2}) = \frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}x^{2})$$
SND의 c.d.f는 다음과 같습니다. (값은 표로 주어집니다.)
$$ \Phi(x) = \int_{-\infty}^{x}\phi(u)du$$
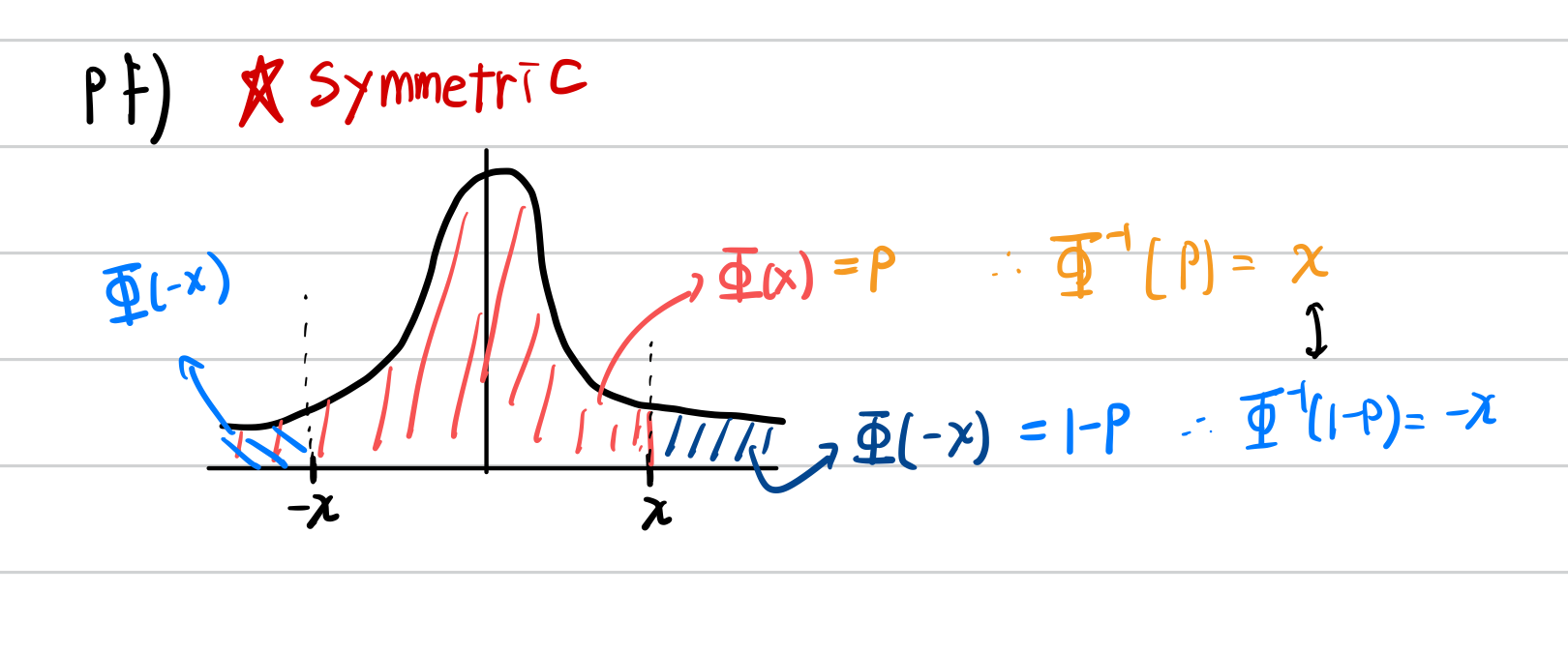
SND의 속성
모든 x와 0<p<1인 p에 대해 다음이 성립합니다.
$$\Phi(x) = 1 - \Phi(-x)$$
$$\Phi^{-1}(p) = - \Phi^{-1}(1-p)$$
증명은 정규분포 그래프가 대칭(Symmetry)임을 이용하여 할 수 있습니다.
정규분포로부터 SND로의 변환
확률변수 X가 다음 정규분포를 따른다고 하겠습니다.
$$X \sim N(\mu, \sigma^{2})$$
이때 다음과 같이 정의된 Z는 SND를 가집니다.
$$Z = \frac{(X - \mu)}{\sigma} $$
X가 반드시 정규분포를 따라야 성립합니다.
증명)
$$X\; \sim \; N(\;\mu, \; \sigma^{2} \;)$$
$$Z = \frac{X-\mu}{\sigma} = \frac{1}{\sigma}X - \frac{\mu}{\sigma}$$
$$Z \;= \;\frac{1}{\sigma}X - \frac{\mu}{\sigma} \;\; \sim \; N(\; \frac{1}{\sigma}\mu \;+\; (-\frac{\mu}{\sigma} ), \; (\frac{1}{\sigma})^{2} \cdot \sigma^2 \;)=N(0, 1^{2})$$
또한 X에 대한 c.d.f를 F라 정의하면, 다음이 성립합니다.
$$F(x) = \Phi(\frac{(x - \mu)}{\sigma})$$
증명)
$$F(x) = P(X \leq x ) = P(Z \leq \frac{(x - \mu)}{\sigma} )$$
예시)

정규분포를 갖는 독립적 확률변수들의 선형조합
(Linear Combination of independent Normally Ditributed Variables)
다음과 같은 k개의 독립(independent)인 확률변수들이 존재한다고 하면,
$$X_1, X_2, ... , X_k \;\;\; where \;\; \forall i\;\;\; X_i \sim N(\mu_i, \sigma_i^{2})$$
이들의 합 역시 정규분포를 따르며, 다음과 같습니다.
$$X_1 + X_2 + \cdots + X_k \sim N(\;\mu_1 + \mu_2 +\cdots + \mu_k, \;\;\; \sigma_1^{2} + \sigma_2^{2} + \cdots + \sigma_k^{2}\;)$$
증명)
X_i의 m.g.f를 다음과 같이 정의합니다.
$$\psi_i(t)$$
이때 X_i는 모두 정규분포를 가지므로, 정규분포의 m.g.f를 이용하면 다음과 같습니다.
$$\psi_i(t) = exp(\mu_it + \frac{1}{2}\sigma^{2} t^{2})$$
이때 각각의 확률변수들의 합에 대한 m.g.f를 정의하면, 다음과 같습니다.
$$\psi = m.g.f \;\; of \;\; \sum^{k}_{i=1}X_i$$
그리고 각각의 확률변수들은 모두 독립(independent)이므로, m.g.f의 특성을 사용하여 다음과 같이 유도가 가능합니다.
$$\psi(t) = \prod_{i=1}^{k}\psi_{i}(t)=\prod_{i=1}^{k}exp(\mu_i t + \frac{1}{2}\sigma^{2}_it^{2})$$
$$\prod_{i=1}^{k}exp(\mu_i t + \frac{1}{2}\sigma^{2}_it^{2}) = exp(\;(\sum^{k}_{i=1}\mu_i) t + \frac{1}{2}(\sum_{i=1}^{k}\sigma_i^{2})t^{2})$$
$$\therefore X_1 + X_2 + \cdots + X_k \sim N(\sum_{i=1}^{k}\mu_i\; ,\; \sum_{i=1}^{k}\sigma_i^{2})$$
또한 위 정리에 따라서 다음 정리도 유도됩니다.
k개의 독립인 확률변수와, 상수들에 대해, 다음과 같이 정의되었을 때,
$$X_1, X_2, ... , X_k \;\;\; where \;\; \forall i\;\;\; X_i \sim N(\mu_i, \sigma_i^{2})$$
$$a_1, a_2, ... ,a_k, b \;\;\; are \; constant$$
다음과 같습니다.
$$a_1X_1 + a_2X_2 + \cdots + a_kX_k + b \;\sim\; N(\;a_1X_1 + a_2X_2 + \cdots + a_kX_k + b, \;\;\;\; a_1^{2}\sigma_1^{2} + a_2^{2}\sigma_2^{2} + \cdots + a_k^{2}\sigma_k^{2}\;)$$
예시)

'🖥 Computer Science > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] - (12) Markov’s inequality(마르코브 부등식), Chebyshev's inequality(체비쇼프 부등식) (0) | 2022.05.16 |
|---|---|
| [확률과 통계] - (11) Sample Mean(표본평균) (0) | 2022.05.09 |
| [확률과 통계] - (9) 여러가지 확률분포 (0) | 2022.04.28 |
| [확률과 통계] - (8) Covariance(공분산) & Correlation coefficient(상관계수) (0) | 2022.04.18 |
| [확률과 통계] - (7) Moments(적률), m.g.f(적률생성함수), median(중앙값) (0) | 2022.04.17 |