🧐 Experiment
결과가 미리 정해져 있지 않고 무작위로(random) 결정되는 현상을 관찰하는 과정(Progress)을 의미합니다.
Experiment를 통해 발생할 수 있는 결과는, 반드시 실험 후 식별될 수 있어야 합니다.
예를 들어 과학 실험에서는 어떠한 결과가 나올 지 예상하기 어렵기에, 과학에서의 Experiment과 확률(Probability)에서의 Experiment는 그 의미가 다릅니다.
확률에서의 정의는 실험 전 그 결과를 예상할 수 있어야 하며, 그 결과가 실험을 통해 식별될 수 있을 때, 비로소 그것이 Experiment라 불리는 것입니다.
예를 들어 주사위를 던지는 Experiment에서의 Output은 다음과 같습니다.
1, 2, 3, 4, 5, 6
그리고 위를 실험의 결과(Output of the experiment)라고 합니다.
🧐 Sample Space (표본공간)
표본공간(Sample Space) 는 결과(output)들이 랜덤하게 발생하는 Experiment의 가능한 모든 결과들의 집합을 의미합니다.
표본공간은 기호로 보통 S를 사용합니다.
주사위를 던지는 Experiment를 예시로 들면, 이때의 Sample Space는 다음과 같습니다.
$$S = \left\{1,2,3,4,5,6\right\}$$
🧐 Event (사건)
사건(Event)의 정의는 다음과 같습니다.
실험을 통해 발생할 수 있는 잘 정의된(well-defined) 결과들의 집합입니다.
👉 well-defined
어떠한 개념의 정의가 어떤 유일한(unique) 해석이나 값을 가리켜,
모순이나 애매함을 내포하지 않는다는 것을 이르는 말입니다.
(좀 더 쉽게 설명하자면, Well - defined Set은 항상 같은 결과가 나옵니다.)
예를 들어 1~10까지의 자연수들이 들어있는 Sample Space에 대해,
'큰 자연수의 집합' 이라는 조건은 Well - defined가 아니며,
'2보다 큰 자연수의 집합'은 Well - defined입니다.
Event는 Sample Space의 부분집합(Subset)이며, 보통 A, B, C (혹은 E) 등으로 표현합니다.
$$A \subseteq C$$
또한 Sample Space 역시 Event입니다.
이제 Sample Space와 Event의 관점에서 Set에 대한 이론들에 대해 살펴보도록 하겠습니다.
🧐 집합 이론 (Set theory)
집합은 확률과 통계를 학습하는 데 있어서 기본적인 개념입니다.
위에서 배운 Sample Space(표본공간)는 전체집합과 동일한 의미를 가지며, Event(사건)은 집합과 동일한 의미를 가집니다.
이곳에서는 확률과 통계를 본격적으로 학습하기 전에 집합에 대한 기본적인 개념과 성질에 대해 알아보도록 하겠습니다.
(이곳의 예시는 특별한 언급이 없는 한 주사위를 던지는 Experiment를 가정합니다.)
🧐 부분집합 (Subset) [ ⊂ ]
두 집합 A와 B에 대해 집합 A의 모든 원소가 집합 B에 속할 때, 집합 A를 집합 B의 부분집합이라고 합니다.
기호로는 다음과 같이 나타냅니다.
$$A \subset B$$
👉 부분집합의 특징 (Property of Subset)
Event A, B, C와 S(Sample Space)가 있을 때,
$$1) \;\; A \subset S$$
$$2) \;\; if\;\; A \subset B \;\; and \;\; B \subset C \;\; then \;\; A \subset C$$
$$3) \;\; if\;\; A \subset B \;\; and \;\; B \subset A \;\; then \;\; A = B$$
예시) 주사위를 던질 때
A : Even number in obtained (짝수만 포함된 집합)
B : a number greater than 1 is obtained (1보다 큰 수들의 집합)
A = { 2, 4, 6 }
B = { 2, 3, 4, 5, 6 }
=> A ⊂ B
🧐 공집합(Empty set) [ Ø ]
다음과 같은 경우, Event는 발생할 수 없다는 뜻입니다.
$$E = \varnothing $$
예시)
C : 7 이상인 수가 나오는 사건
-> C = Ø(Empty Set)
🧐 여집합 (Complement) [A^c]
어떠한 사건 A에 대하여, A가 발생하지 않는 사건은 다음과 같이 표현합니다.
$$A = \;\; event \; A^{c} $$
예시)
A = 짝수가 포함되는 사건 -> A = { 2, 4, 6 }
=> Ac = 짝수가 포함되지 않는 사건 -> Ac = { 1, 3, 5 }
👉 여집합의 특징 (Property of Complement)
$$(A^{c})^{c} = A, \;\;\; \varnothing^{c} = S, \;\;\; S^{c} = \varnothing $$
🧐 합집합 (Union) [∪]
사건 A와 B에 대하여, A또는 B, 혹은 A와 B가 같이 발생하는 사건은 다음과 같이 정의됩니다.
$$A \cup B$$
👉 합집합의 특징 (Property of Union)
$$1) \;\; A \cup B = B \cup A$$
$$2) \;\; A \cup A = A$$
$$3) \;\; A \cup A^{c} = S $$
$$4) \;\; A \cup \varnothing = A $$
$$5) \;\; A \cup S = S$$
$$6) \;\; if \;\; A \subset B \;\; then \;\; A \cup B = B$$
$$7) \;\; A \cup B \cup C = (A \cup B) \cup C = A \cup (B \cup C) $$
🧐 교집합(Intersection) [ ∩ ]
A와 B가 같이 일어나는 사건은 다음과 같이 표현합니다.
$$A \cap B$$
예시)
A = 짝수가 포함되는 사건 -> A = { 2, 4, 6 }
B = 4 미만의 수가 포함되는 사건 -> B = { 1, 2, 3 }
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∩ B = { 2 }
👉 교집합의 특징(Property of Intersection)
$$1) \;\; A \cap B = B \cap A$$
$$2) \;\; A \cap A = A$$
$$3) \;\; A \cap A^{c} = \varnothing $$
$$4) \;\; A \cap \varnothing = \varnothing $$
$$5) \;\; A \cap S = A$$
🧐 서로소 (disjoint)
서로소의 정의는 다음과 같습니다.
$$if \;\; A \; and \; B \;\; are\; disjoint\;\; \to \; A \cap B = \varnothing $$
그리고 다음이 성립합니다.
$$A_1, A_2, ..., A_n \;\; are\;\; mutually\;\; disjoint \;\; = \forall_{i,j}\;\; A_i \cap A_j = \varnothing$$
🧐 집합의 추가적인 속성
1) 드모르간 법칙 (De Morgan's law)
$$(A \cup B)^{c} = A^{c} \cap B^{c}$$
$$(A \cap B)^{c} = A^{c} \cup B^{c} $$
2) 분배 법칙 (Distribute property)
$$A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$$
$$A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$$
3) 집합의 분할 (Partitioning a Set)
👉 Partition?
집합 U에 대해서, U가 다음과 같이 분할된다면,
$$P_1, P_2, ... P_n$$
각각의 P는 Partition이며 따라서 각각의 P는 disjoint(서로소)입니다.
따라서 다음이 성립합니다.
$$P_1 \cup P_2 \cup ... \cup P_n = U$$
$$\forall_{i,j} \to P_i \cap P_j = \varnothing$$
👉 Property
$$1) \;\; A = ( A \cap B ) \cup ( A \cap B^{c} ) $$
(이때 A ∩ B , A ∩ Bc 는 partition of A, 따라서 A ∩ B , A ∩ Bc는 disjoint 입니다 )
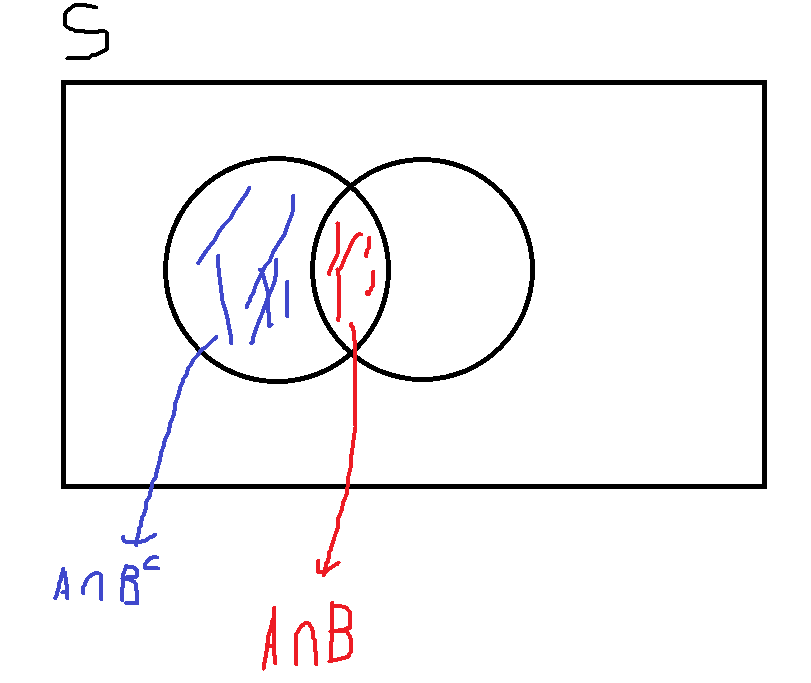
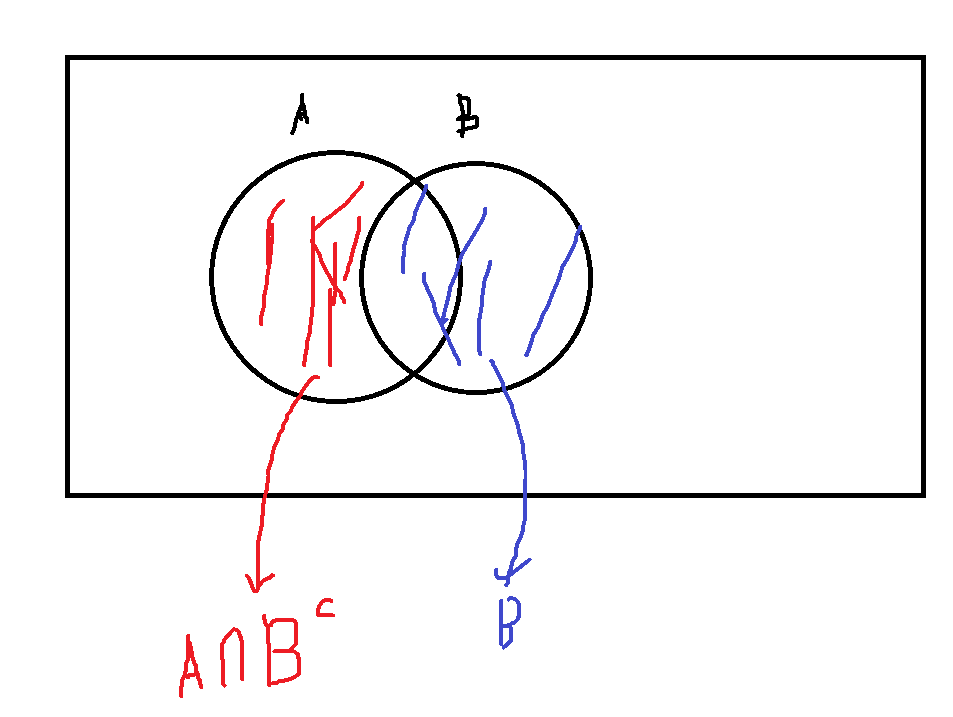
$$2) \;\; A \cup B = B \cup ( A \cap B^{c} )$$
🧐 확률의 (공리적)정의 (The definition of Probability)
확률의 공리적 정의는 다음과 같이 아래 3가지의 공리(axioms)를 만족시키는 값으로 정의됩니다.
👉 Axioms (공리)
$$1) \;\; \forall A \subset S, \;\; then \;\; 0 \leq P(A)$$
$$2) \;\; P(S) = 1$$
3)모든 쌍마다 서로소( mutually disjoint)인 사건들의 셀 수 있는 무한한 열(countable infinite sequence)에 대하여, 다음이 성립합니다.
$$P(\bigcup_{i=1}^{\infty}A_i) = \sum_{i=1}^{\infty}P(A_i)$$
3번은 또한 다음과 같이도 정의됩니다.
for any finite collection of events A1,... An if they are mutally disjoint, 다음이 성립한다
$$P(\bigcup_{i=1}^{n}A_i) = \sum_{i=1}^{n}P(A_i)$$
👉 countable infinite
포함 : N(Natural number(자연수)), Z(Integers(정수)), R (Rational number(유리수))
비포함 : Irrational(무리수), Real(실수)
👉 확률의 속성 (Property of Probability)
$$1) \;\; P(\varnothing) = 0$$
증명)
consider countable infinite collection of sets A1, A2, ... ,
모든 i에 대해서 Ai= Ø 이라면
모든 i,j에 대해서, Ai ∩ Aj = Ø 이며, 이는 mutually disjoint 입니다.
따라서 3번째 Axiom에 의하여
$$P(\varnothing ) = P(\bigcup_{i=1}^{\infty}A_i) = \sum_{i=1}^{\infty}P(A_i) = \sum_{i=1}^{\infty}P(\varnothing)$$
이며, 무한대로 같은 값을 더했을 때, 하나의 값이 되는 수는 0밖에 없습니다.
🧐 Other Property
$$1) \;\; P(A^{c}) = 1 - P(A)$$
👇 증명
A와 A^c는 mutually disjoint 이므로
$$P(A \cup A^{c}) = P(A) + P(A^{c}) \;\;\; by\;\; Axiom(3)$$
$$이때 \;\;P(A \cup A^{c}) = P(S) =1 = P(A) + P(A^{c})$$
$$P(A^{c}) = 1-P(A)$$
$$2) \;\; if \;\; (A \subset B) \;\;then \;\;P(A) \leq P(B)$$
👇 증명
$$A \subset B \;\;이므로\;\; B = A \cup (B \cap A^{c})$$
$$이때 \;\; A \;\; and \;\; B \;\; are \;\; disjoint$$
$$따라서 \;\; P(B) = P(A) + P(B \cap A^{c}) \;\;\; by \;\; Axiom(3)$$
$$ 0 \leq \;P(B \cap A^{c}) \;\;\; by\;\;Axiom(1)$$
$$P(B) \geq P(A)$$
$$3) \;\; 0 \leq P(A) \leq 1$$
👇 증명
$$P(S) = 1, \;\; A \subset S \;\; by Axiom(2)$$
$$P(A) \leq P(S) \;\;\; by \;\; property \;\; 2$$
$$또한 \;\;0 \leq P(A) \;\; by\;\;Axiom(1) $$
$$0 \leq P(A) \leq 1$$
$$4) P(A \cap B^{c}) = P(A) - P(A \cap B)$$
👇 증명
$$A = (A \cap B) \cup (A \cap B^{c})$$
$$A \cap B \;\; and\;\; A \cap B^{c}\;\; are\;\; disjoint$$
$$P(A) = P(A \cap B) + P(A \cap B^{c}) \;\; by \;\;Axiom(3)$$
$$P(A \cap B^{c}) = P(A) - P(A \cap B)$$
$$5) \;\; P(A \cup B) = P(A) \cup P(B) - P(A \cap B)\;\; 포함-베제 원리$$
👇 증명
$$A \cup B = B \cup (A \cap B^{c})\;\;이고$$
$$B \;\; and \;\; (A \cap B^{c}) \;\; are\; disjoint$$
$$P(A \cup B) = P(B) + P(A \cap B^{c}) = P(B) + P(A) - P(A \cap B) \;\; by\;\; Axiom(3)$$
예시)
사탕 또는 초콜릿을 좋아하는 학생이 있다.
S = { candy, chocolate }
P({candy}) = 0.3
P({chocolate}) =0.8
P( A student likes both candy and chocolate ) : ???
P(S) = P( A ∪ B )이며
P( A ∪ B ) = P(A) + P(B) - P ( A∩B ) 이다.
따라서 1= 0.3 + 0.8 - x,
따라서 x = 0.1
🧐 Bonferroni inequality
모든 event에 대해(서로소(disjoint) 조건이 없는, 셀 수 있는 유한, 혹은 제한된 집합에 대해), 적어도 하나의 사건이 발생할 확률은 개별 사건의 확률의 합보다 더 클 수 없음을 말합니다.
즉 다음과 같이 표현합니다.
$$P(\bigcup_{i=1}^{n}A_i) \leq \sum_{i=1}^{n}P(A_i)$$
증명은 귀납법을 사용하여 할 수 있습니다.

🧐 확률이 0인 사건
불가능한 사건은 확률이 0입니다.
그러나 확률이 0인 사건은 불가능한 사건이 아닙니다.(아니다 보다는 아닐수도 있다는 뜻입니다!)
조금 더 자세히...
기하학적 확률 혹은 공리적 확률에 따르면, 확률 0은 단지영역의 넓이 혹은 측도가 0인 것 뿐입니다.
더욱 구체적으로 이야기해 보면, 수직선 위의 선분 [0, 1] 위에서 균등하게 점을 뽑는다고 생각을 했을 때, 한 점을 뽑을 확률은 0이 되지만, 어쨌거나 한 점은 뽑히게 되어있습니다.
따라서 '확률이 0인 사건은 일어나지 않는다'라고 가정해 버리면 '선분 위에서 점을 뽑을 수 없다'는 이상한 결론이 나와 버리는 것입니다.
하지만 '통계적 확률의 의미로 생각해보면 한번 일어난 사건이 확률 0인 건 말이 안되지 않느냐?' 고 물어볼 수 있지만, 이것도 반박이 되는 것이 통계적 확률은 무수한 시행에서 평균의 극한을 생각하기 때문입니다.
이를 선분 예시로 본다면 [0, 1]에서 수 x를 뽑았다면 x를 뽑은 사건은 일단 일어났지만, 이 시행을 몇 번이고 반복해도 그 정확한 x를 뽑을 일은 앞으로는 일어나지 않을 것입니다.
따라서 사건이 일어났음에도 통계적 확률이 0인 것은 전혀 부자연스럽지 않닙니다.
Reference
http://www.kocw.net/home/search/kemView.do?kemId=1056974
확률 및 통계
확률변수는 예측할 수 없는 물리적 신호를 표현하는 수학적 모델로서, 함수의 변수가 확률적 분포에 의하여 임의로 발생하는 경우에 적용한다. 확률신호는 통신신호, 영상 및 음성신호, 등과 같
www.kocw.net
https://en.wikipedia.org/wiki/Boole%27s_inequality
Boole's inequality - Wikipedia
In probability theory, Boole's inequality, also known as the union bound, says that for any finite or countable set of events, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events.
en.wikipedia.org