Multiple Random Variables
지금까지는 하나의 특정한 확률변수(RV)에 대한 확률이 얼마가 되는지만 구해보았습니다.
또한 pdf(Probability Density Function)에서는 X라는 RV의 값이 특정함 범위 안에 들어있을 확률을 구했었습니다.
그러나 이번에는 확률변수가 2개인 경우에 대해서의 확률에 대해서 알아보겠습니다.
Joint distribution (결합분포)
2개 이상의 확률 변수(multiful r.v.s)에 의한 분포입니다.
X, Y라는 두개의 확률변수가 있을 때, X와 Y의 결합분포는 다음과 같습니다.
$$P(X = x_1, Y = y_1)$$
이러한 경우 Sample Space(표본공간)는 X가 정의된 Sample Space와 Y가 정의된 Sample Space의 카테시안 곱(즉 순서쌍)으로 확장됩니다.
따라서 Sample Space가 확장됐기에, 확률변수의 치역도 X와 Y의 치역의 카테시안 곱으로 확장됩니다.
우선 여러개의 확률변수(r.v.s)에 대한 CDF를 알아보도록 하겟습니다.
marginal distribution (주변분포)
여러개의 확률 변수로 이루어진 Joint c.d.f나 p.d.f, p.m.f가 있을 때 각각의 변수 하나하나에 대한 c.d.f, p.d.f 또는 p.f에 Marginal 이라는 단어를 붙여서 표현합니다.
또한 Marginal Distribution을 구하고 싶은 경우, 구하고 싶은 변수 이외의 다른 값의 모든 경우를 다 고려해준다면 구하고 싶은 변수에 대한 dritribution을 구할 수 있습니다.
예를 들어 Joint c.d.f 인 경우
$$F_x(x) = F_{xy}(x, \infty)$$
$$F_y(y) = F_{xy}(\infty, y)$$
Joint Cumulative Distribution Function (Joint CDF, 결합 누적분포함수)
Joint CDF를 다음과 같이 표현하겠습니다.
$$F_{xy}(x, y)\overset{\underset{\mathrm{def}}{}}{=}P(X\leq x, Y \leq y)$$
이것(cdf)이 의미하는 것은 아래 표시된 부분의 영역에 x, y 좌표가 들어오게 될 확률입니다.
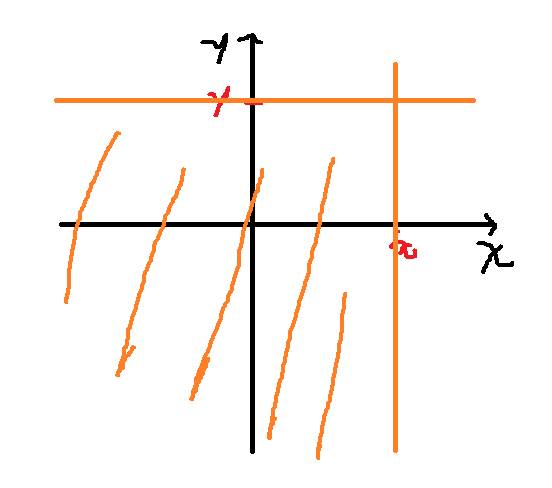
Joint CDF의 특징들을 알아보도록 하겠습니다.
Properties of Joint CDF
1) CDF도 확률이기 때문에 아래가 성립합니다.
$$ 0\leq F_{xy}(x, y)\leq 1 $$
2) Joint CDF는 non-decreasing surface입니다. 따라서
$$for \quad x_1 < x_2, \; y_1 < y_2 $$
$$ F_{xy}(x_1, y_1) \leq F_{xy}(x_1, y_2) \leq F_{xy}(x_2, y_2)$$
$$ F_{xy}(x_1, y_1) \leq F_{xy}(x_2, y_1) \leq F_{xy}(x_2, y_2)$$
(surface라고 표현한 것은 function이라 표현한 경우 곡선등을 생각할 것이기 때문에, 이를 명확히 하기 위해 surface라고 표현하였습니다. RV가 1개일 때는 CDF는 곡선으로 표현되지만, RV가 2개일 경우 CDF는 곡면으로 표현됩니다.)
아래는 이해를 돕기 위한 Joint CDF의 그림입니다.
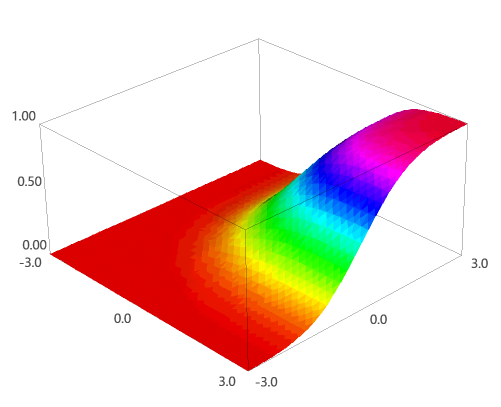
$$3) \;\;\; \displaystyle \lim_{ {x\to \infty \; y\to \infty}}F_{xy} = P(X\leq \infty , Y\leq \infty) = 1$$
$$4) \;\;\;\displaystyle \lim_{ {x\to -\infty }}F_{xy} = P(X\leq -\infty , Y\leq y) = 0$$
$$\displaystyle \lim_{ {y\to -\infty }}F_{xy} = P(X\leq x , Y\leq -\infty) = 0$$
$$5) \;\;\;P(x_1 < X \leq x_2,\; Y\leq y)$$ 위 식은 아래 면적의 넓이를 구하는 것입니다.
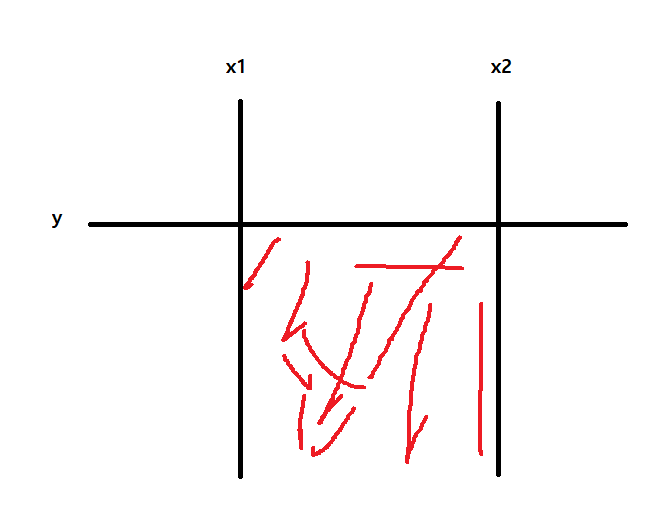
즉 다음과 같습니다.
$$F_{xy}(x_2, y) - F_{xy}(x_1, y)$$
$$6) \;\;\;P(x_1 < X \leq x_2,\; y_1<Y\leq y_2)$$ 위 식은 아래 주황색 부분의 면적의 넓이를 구하는 것입니다.
(사실 부피를 구하는 것이나, 좀 더 편하게 이해하기 위해 평면으로 그렸습니다.)
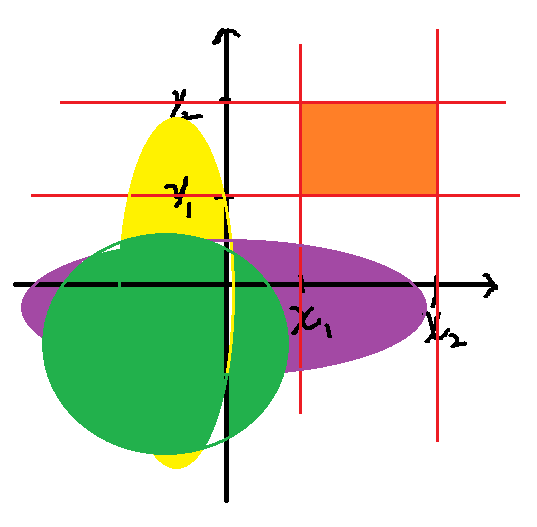
즉 다음과 같습니다.
$$F_{xy}(x_2, y_2) - F_{xy}(x_1, y_2)- F_{xy}(x_2, y_1) + F_{xy}(x_1, y_1)$$
marginal CDF
Joint CDF에 대해서 다른 변수를 무한대로 보내버리면(즉 모든 조건을 다 생각한다면) 나머지 변수에 대한 marginal CDF를 얻을 수 있습니다.
$$F_x(x) = F_{xy}(x, \infty)$$
$$F_y(y) = F_{xy}(\infty, y)$$
Joint Probability Mass Function (Joint p.m.f , p.f)
2개의 Discrete Random Variables에 대한 확률분포 즉 Joint Probability Mass Function은 다음과 같이 정의됩니다.
$$\forall{(x, y) \in R^{2} } , \;\;\; f(x,y) = P(X=x \;and \; Y = y)$$
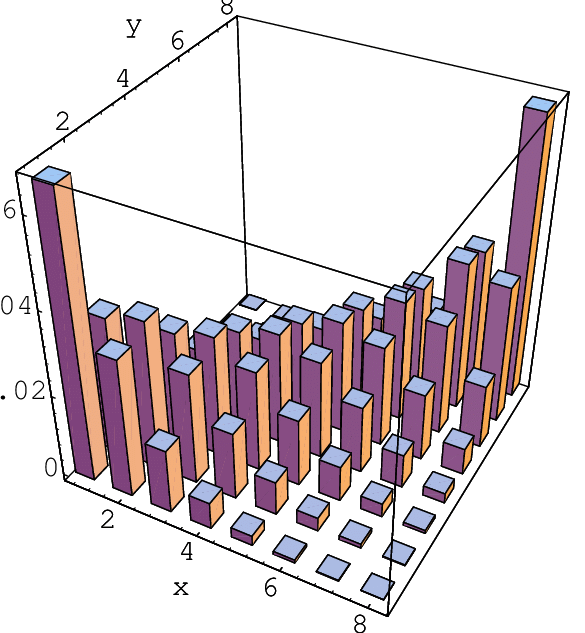
X = x 인 경우의 확률과 Y = y인 경우의 확률을 구해서 곱하면 되지 않을까란 생각을 할 수도 있는데, 이는 Independent한 상황에서만 성립하며, 일반적으로는 성립하지 않습니다.
Properties of Joint PMF
1)만약 (X , Y)가 순서쌍 (x, y)를 갖지 않는다면, 해당 확률은 0입니다.
$$if\;\; (X, Y)\;\; cannot \;\; have \;\; a \;\; ordered\;\; pair\;\; (x,y) \;\; then \;\;f(x, y) = 0 $$
2) 모든 (X, Y) 순서쌍의 확률을 더한 값은 1입니다.
$$\sum_{x}^{}\sum_{y}^{} P_{xy}(x,y)=1$$
3) 확률이므로 0과 1 사이의 값을 가집니다.
$$0\leq p_{xy}(x, y)\leq 1$$
4)누적분포함수는 다음과 같이 구합니다.
$$F_{xy}(x,y) = P(X \leq x, Y \leq y) = \sum_{X\leq x}^{}\sum_{Y\leq y}^{}P_{xy}(x,y)$$
marginal PMF
$$P_x(x)=\sum_{y}^{}P_{xy}(x,y)$$
$$P_y(y)=\sum_{x}^{}P_{xy}(x,y)$$
Independent 인 경우
$$P_{xy}(x, y)=P_x(x) P_y(y)$$
Joint Probability Density Function (Joint p.d.f)
아래와 같은 음이 아닌 함수 f를 가질 때, X와 Y는 continuous joint distribution 를 가진다고 합니다.니다.
$$P((X,Y) \in C \subset R^{2}) = \int_{C} \int f(x, y) dxdy$$
그리고 이때의 f를 joint probability density function (joint p.d.f)라고 합니다.
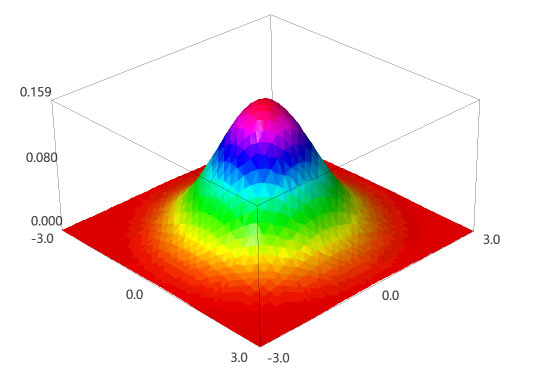
PDF는 CDF를 미분하면 구할 수 있었습니다. 따라서
$$f_{xy}(x,y) \overset{\underset{\mathrm{def}}{}}{=} \frac{\partial^{2} F_{xy}(x,y)}{\partial x \partial y }$$
또한 CDF는 PDF를 적분하면 구할 수 있으므로
$$F_{xy}(x, y) = \int_{-\infty}^{y} \int_{-\infty}^{x} f_{xy}(u ,v)dudv$$
Properties of Joint PDF
1) x y 평면의 모든 각각의 한 점(point)에서의 확률은 0입니다.
2)(x, y)가 평면이 아닌 하나의 직선 위에 존재할 경우, 이에 대한 확률은 0입니다.
$$when \;\; C = \left\{ (x, y) | y =f(x) \right\} \;\; or \;\; C = \left\{ (x, y) | x =f(y)\right\} $$
$$then \;\; \int \int f(x, y)dxdy = 0$$
3) 확률이므로 다음이 성립합니다.
$$)1 \geq f(x, y ) \geq 0$$
4) 모든 경우의 확률을 다 더한 값은 1입니다.
$$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f_{xy}(x, y)dxdy = 1 = F_{xy}(\infty, \infty)$$
5) (X, Y)가 특정 구간에 존재할 확률은 다음과 같이 구합니다.
$$P(x_1 < X\leq X_2, y_1< Y\leq y_2) = \int_{y_1}^{y_2}\int_{x_1}^{x_2}f_{xy}(x,y)dxdy$$
$$= F_{xy}(x_2, y_2)-F_{xy}(x_1, y_2) - F_{xy}(x_2, y_1) + F_{xy}(x_1, y_1)$$
또한 이곳에서 이중적분은 부피를 구하는 것을 의미합니다
marginal PDF
$$f_x(x) = \int_{-\infty}^{\infty} f_{xy}(x, y) dy$$
$$f_y(y) = \int_{-\infty}^{\infty}f_{xy}(x,y)dx$$
Independent 인 경우
$$f_{xy}(x, y) =f_x(x)f_y(y)$$
또한 x와 y의 범위가 unbounded한 경우(x >=0, y>=0),
$$f(x, y) = h(x)\cdot h(y)$$ 일때,
h(x)는 오직 x에 의해서만 영향을 받고, h(y)는 y에 의해서만 영향을 받으므로,
X와 Y는 independent 합니다.
예제
1개의 동전을 3번 던진다고 가정해 보겠습니다.
X : 맨 처음 동전이 H가 나오면 1, T가 나오면 0
Y : 총 H가 나온 횟수
이는 다음과 같습니다.
$$P_x(0) = \frac{1}{2}, \; P_x(1) = \frac{1}{2}, \;\;P_y(0) = \frac{1}{8}, \; P_y(1) = \frac{1}{4}, \;\;P_y(2) = \frac{1}{4}, \; P_y(3) = \frac{1}{8},$$
| X |Y | 0 | 1 | 2 | 3 |
| 0 | P(0, 0) = 1/8 | P(0, 1) = 2/8 | P(0, 2) = 1/8 | 0 |
| 1 | 0 | P(1, 1) = 1/8 | P(1, 2) = 2/8 | P(1, 3) = 1/8 |
$$\sum_{x=0}^{1}P_x(x) = 1$$
$$\sum_{y=0}^{3}P_y(y) = 1$$
$$\sum_{y=0}^{3}\sum_{x=0}^{1}P_{xy}(x,y) = 1$$
추가로 joint probability 로부터 X에 대한 marginal probability를 구해보겠습니다.
$$P_x(0) = \sum_{y=0}^{3}P_{xy}(0, y ) = \frac{1}{2}$$
$$P_y(2) = \sum_{x=0}^{1}P_{xy}(x, 2 ) = \frac{3}{8}$$
추가로 Independent의 여부를 구해보겠습니다.
$$P_{xy}(0, 2) = \frac{1}{8} $$
$$P_x(0)P_y(2) =\frac{1}{2} * \frac{3}{8} = \frac{3}{16} \neq P_{xy}(0, 2) $$
따라서 X와 Y는 Independent가 아닙니다.
2번
$$P_{xy}(x,y)= k(2x+y)$$
에 대해,
x = 1,2
y = 1,2
이다.
이때 k, marginal Prob, Independent 여부를 구해보겠습니다.
$$\sum_{x=1}^{2}\sum_{y=1}^{2}k(2x+y) = 1$$
이므로,
k(3 + 4 + 5 + 6) = 1이며, 따라서
$$ k = \frac{1}{18}$$
marginal Prob는 다음과 같습니다.
$$P_x(x) = \sum_{y=1}^{2}\frac{1}{18}(2x + y) = \frac{1}{18}(4x+3)$$
$$P_y(y) = \sum_{x=1}^{2}\frac{1}{18}(2x + y) = \frac{1}{18}(2y+6)$$
Independent 여부는 다음과 같습니다
$$\frac{1}{18}(2x+y) \neq \frac{1}{18}(4x+3) * \frac{1}{18}(2y+6)$$
이므로 Independent하지 않습니다.
'🖥 Computer Science > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] - (6) 기댓값(Expectation)과 분산(Variance), LOTUS(Law of the unconscious statistician, 무의식적인 통계학자의 법칙) (0) | 2022.04.10 |
|---|---|
| [확률과 통계] - (5) 조건부 결합확률분포(joint conditional distribution) (2) | 2022.03.31 |
| [확률과 통계] - (3) 확률변수, 누적분포함수(CDF), 이산확률변수, 확률질량함수(pmf) (5) | 2022.03.26 |
| [확률과 통계] - (2) 순열, 조합, 조건부확률, 베이즈 정리 (0) | 2022.03.17 |
| [확률과 통계] - (1) 집합과 확률 (0) | 2022.03.02 |