🧐 Encoding
알파벳 $\Sigma$ 으로 이루어진 문자열에 대하여
0과 1로 이루어진 binary string(혹은 binary code, codeword) 으로 표현하는 것
간단한 예시를 하나 살펴보면 다음과 같습니다.
| Binary code | |
| A | 00 |
| B | 01 |
| C | 10 |
| D | 11 |
위 표에 주어진대로 다음 문자열 (ABBCCDA) 을 인코딩 해보도록 하겠습니다.
| A | B | B | C | C | D | A |
| 00 | 01 | 01 | 10 | 10 | 11 | 00 |
🧐 Decoding
Encoding 된 binary string을 다시 original string으로 나타내는 것을 의미합니다.
위의 예시에서 디코딩 시에는 인코딩된 binary string을 두 character씩 확인하면서 해당 codeword에 대응되는 알파벳으로 바꾸어주면 됩니다.
🧐 Prefix-Free Code
각 code의 길이가 다른 경우에 대하여 인코딩을 생각해 보도록 하겠습니다.
| Binary code | |
| A | 0001 |
| B | 00 |
| C | 01 |
| D | 001 |
주어진 문자열은 ABBCCDA 입니다.
이는 인코딩 하면 다음과 같습니다.
| A | B | B | C | C | D | A |
| 0001 | 00 | 00 | 01 | 01 | 001 | 0001 |
인코딩 시에는 문제가 발생하지 않지만, 디코딩을 해야 하는 경우 문제가 발생합니다.
시작되는 string인 0001을 보면, 이것이 A인지 BC인지 구분할 수가 없습니다.
이를 해결하기 위해서는 어떤 codeword도 다른 codeword의 prefix가 되지 않아야 합니다.
다르게 표현하면 어떤 codeword도 다른 codeword의 prefix가 되지 않는 경우 decoding을 하는 방법이 유일합니다.
이와 같은 codeword를 prefix-free code라 합니다.
예를 들면 다음과 같은 codeword가 있습니다.
| Binary code | |
| A | 0 |
| B | 100 |
| C | 101 |
| D | 11 |
🧐 Prefix-free code와 Full Binary Tree
Prefix-free code의 경우 codeword table을 Full Binary Tree(각 노드의 child가 0개 혹은 2개로만 이루어진 트리)로 나타내는 것이 가능합니다.
우선 트리를 보며 설명을 이어가도록 하겠습니다.
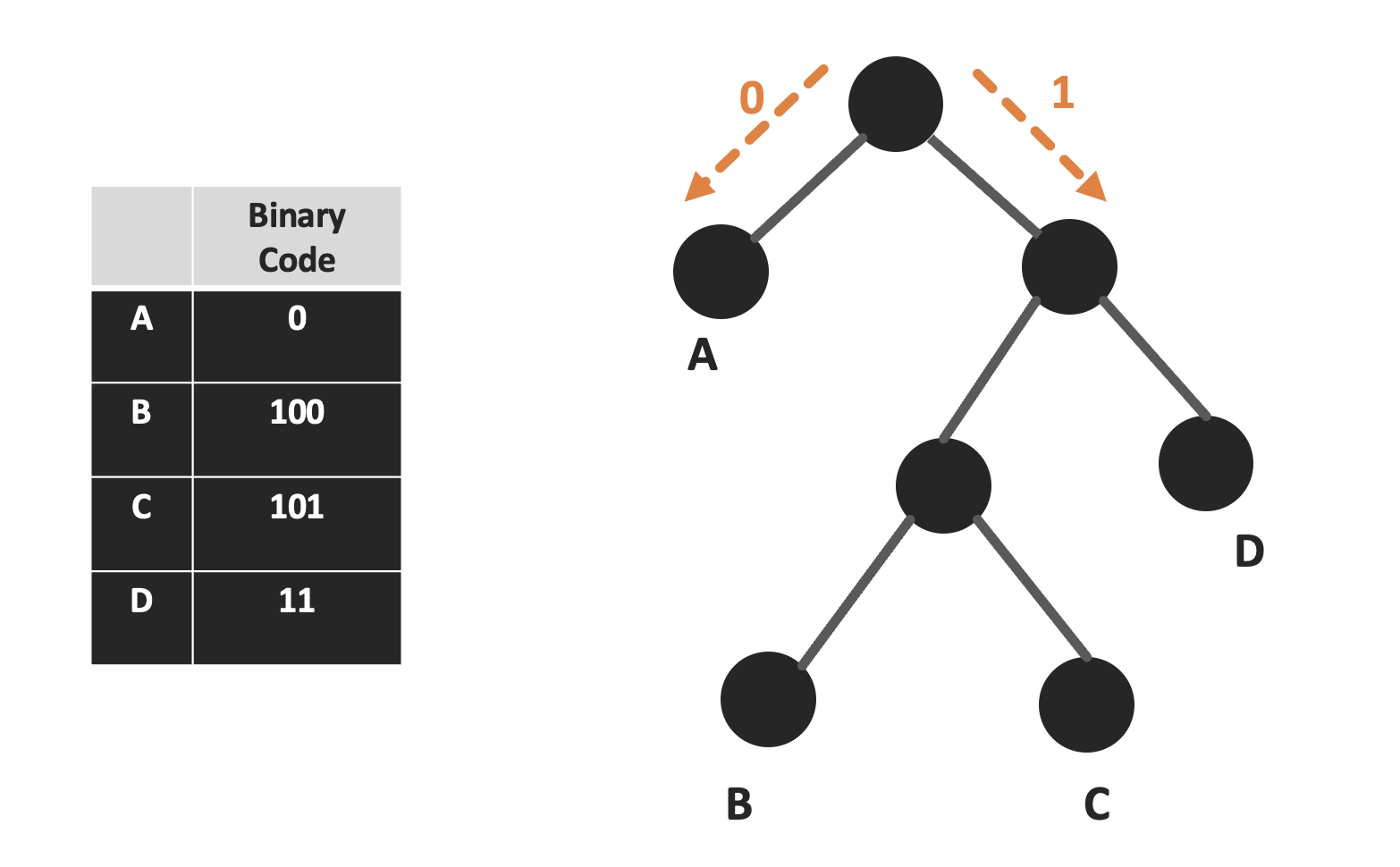
1. Tree의 각 leaf node는 기존 문자열의 각 알파벳에 대응합니다
2. 알파벳 A에 대한 codeword는 tree의 root에서 A까지의 path에 의해 결정됩니다.
3. root에서 leftchild로 갈 경우 cordword 에 0, rightchild로 갈 경우 1을 concatnation 해주는 과정을 통해 codeword를 생성할 수 있습니다.
4. 똑같은 방법으로 decoding 또한 tree만을 이용하여 가능합니다.
⭐️ Fixed-length encoding
각 알파벳에 해당하는 codeword의 길이가 모두 동일한 인코딩을 의미합니다.
Fixed-length encoding을 사용하면 codeword의 길이 단위로 한번에 한 단어씩 디코딩할 수 있으므로 속도가 빠르고 간편합니다.
그러나 문자의 수가 많아지면 codeword의 길이가 늘어나기 때문에 encoding된 결과 문자열의 길이가 매우 길어질 수 있습니다.
⭐️ Variable-length encoding
각 알파벳에 해당하는 codeword의 길이가 다른 인코딩을 의미합니다.
encoding된 결과물의 길이는 짧을수록 좋으며 prefix-free code를 이용하여 encoding을 했을 때 encoding된 결과물의 길이는 다음과 같이 구할 수 있습니다.
$$\Sigma^{n}_{i=1}f_i \cdot (\;depth \; of \; alphabet\; i \; in \;tree\;)$$
이때 $f_i$ 는 기존 문자열에 속한 i의 개수를 의미합니다.
또한 root node의 depth는 0입니다.
🧐 Huffman Encoding
허프만 인코딩의 목적은 Encoding 결과물의 길이가 최소가 되도록 하는 tree를 생성하는 것입니다.
허프만 인코딩에 대응하는 Full Binary Tree를 Huffman tree 라 합니다.
허프만 인코딩은 기본적으로 등장하는 문자의 빈도수가 클수록 대응하는 codeword의 크기를 줄여 전체 결과물의 길이를 줄이는 것입니다.
⭐️ Key Lemma
빈도수(frequency)가 제일 작은 두 leaf node(= alphabet)는 반드시 Huffman tree 에서 제일 큰 depth를 가지고 있어야 합니다.
증명은 귀류법을 통해 가능합니다.
Depth가 가장 큰 두 leaf node $i, j$ 보다 빈도수가 작은 다른 leaf node $k$ 를 가정하겠습니다.
$i$ 와 $k$ 를 Huffman tree에서 교체 시 encoding 결과가 줄어듭니다.
따라서 Huffman encoding이 최적해라는 사실에 모순됩니다.
단계는 다음과 같습니다.
1. 기존 문자열에서 각 알파벳의 빈도를 구합니다.
2. 각각의 알파벳에 해당하는 Leaf Node를 생성합니다.
3. 등장 빈도수가 가장 작은 leaf node 두개를 선택하여 이 둘을 left, right child로 가지는 parent node를 생성합니다.
그리고 해당 노드의 빈도수는 left와 right subtree의 빈도수의 합입니다.
4. node가 하나만 남을 때까지 남아있는 node들에 대하여 (3)을 반복합니다.
⭐️ 예시
예시 문자열은 아래와 같습니다.
BDBBEACDEEAEEDBDCD
우선 해당 문자열에서 각 단어별 빈도수를 구합니다.
| $f_A$ | $f_B$ | $f_C$ | $f_D$ | $f_E$ |
| 2 | 4 | 2 | 5 | 5 |
이제 각각의 알파벳에 해당하는 leaf node를 생성합니다.
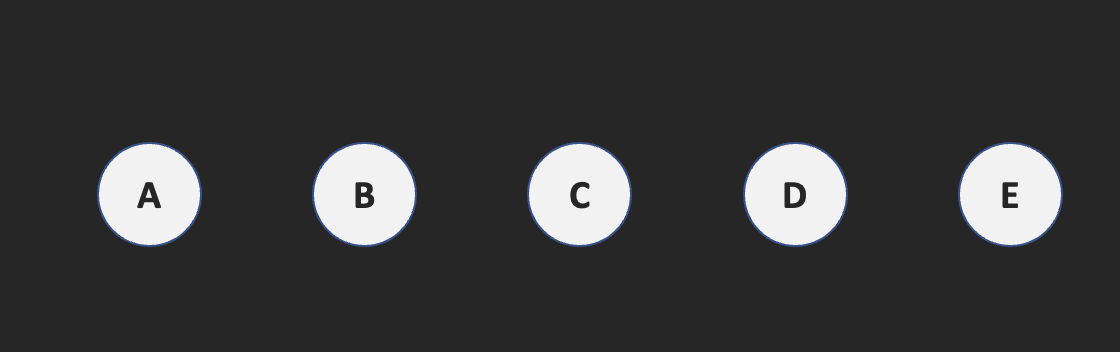
빈도수가 가장 작은 leafnode 두개를 선택하여 이 둘은 left와 right child로 가지는 이진 트리를 생성합니다.
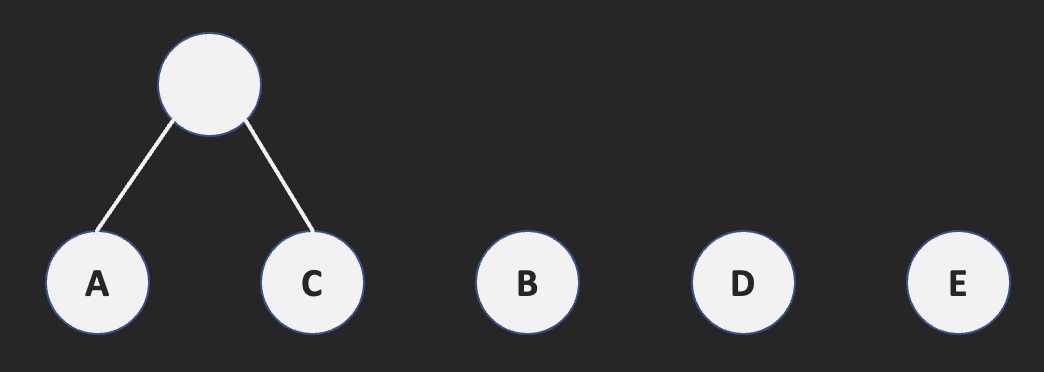
| $f_{A+C}$ | $f_B$ | $f_D$ | $f_E$ | |
| 4 | 4 | 5 | 5 | |
위 과정을 node가 하나만 남을 때까지 계속해서 반복합니다.
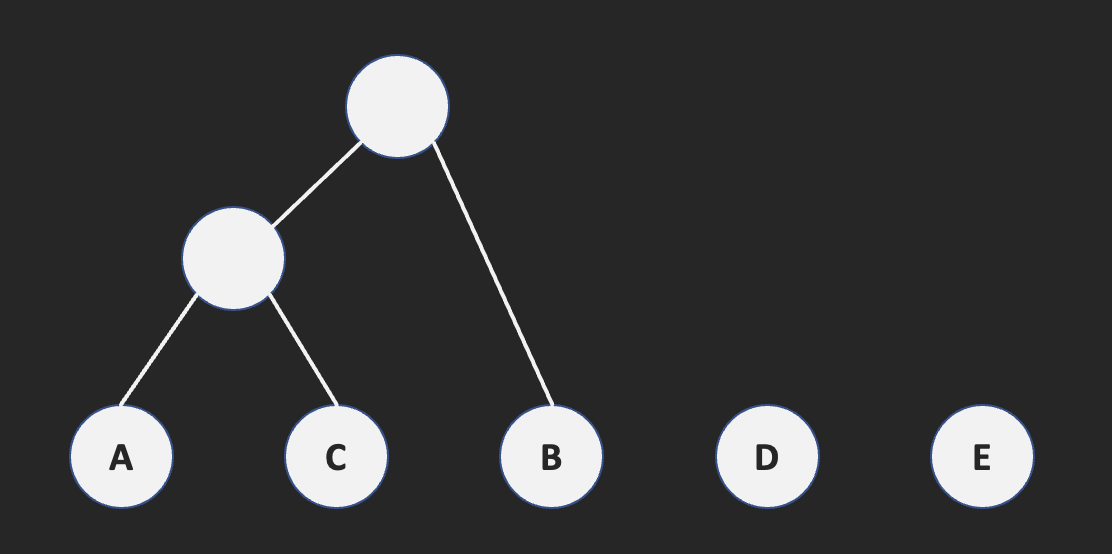
| $f_{A+C+B}$ | $f_D$ | $f_E$ | ||
| 8 | 5 | 5 | ||
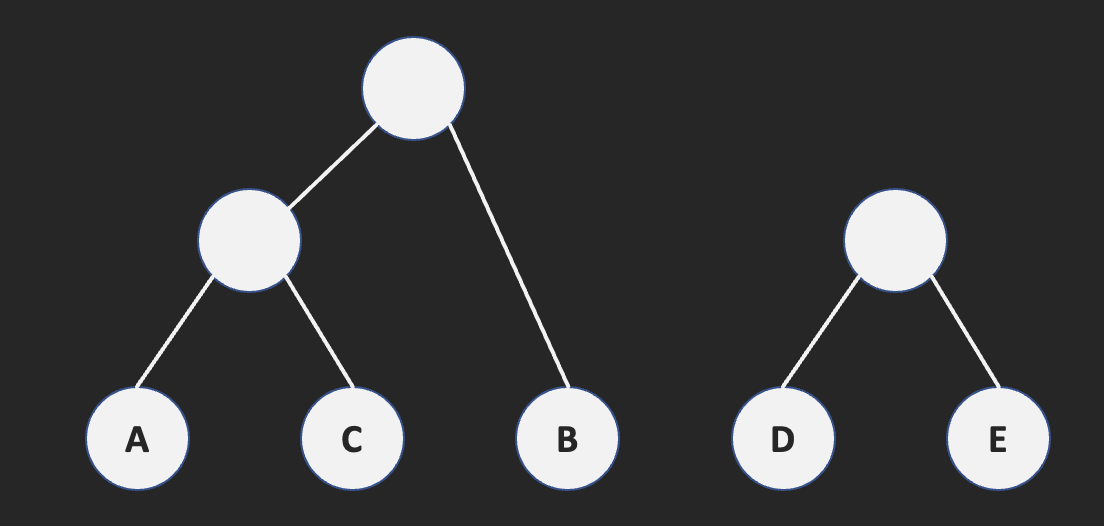
| $f_{A+C+B}$ | $f_{D+E}$ |
| 8 | 10 |
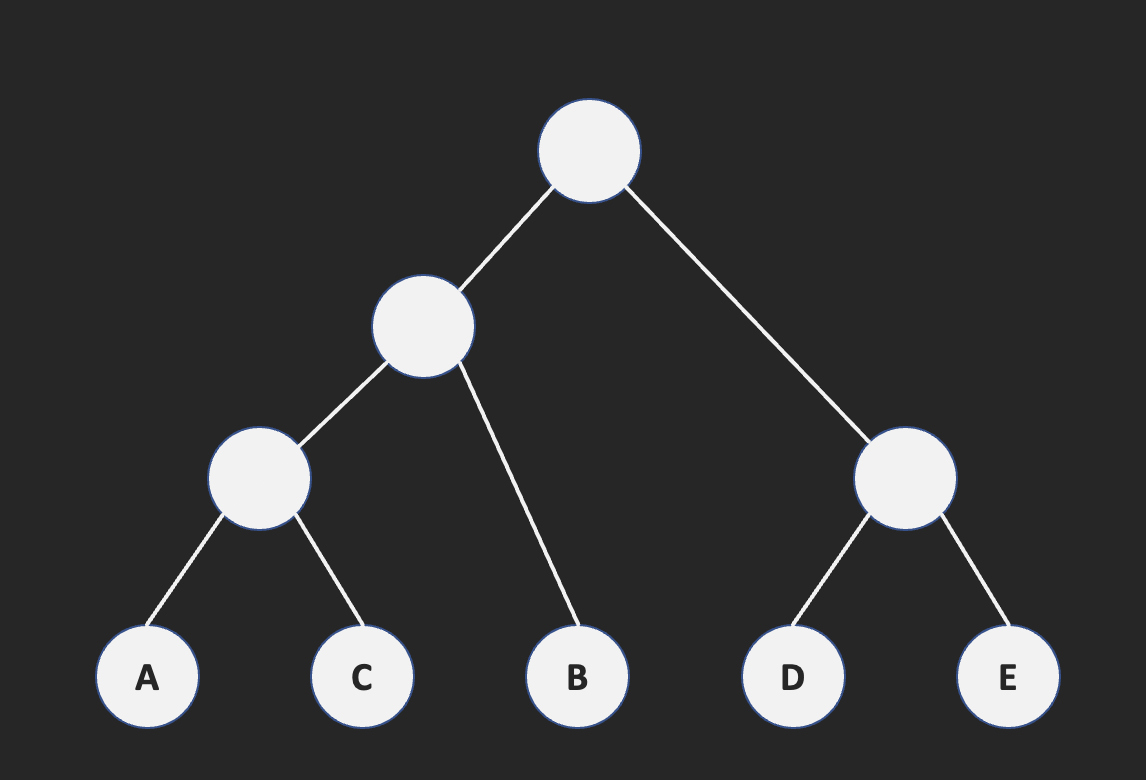
| $f_{A+C+B+D+E}$ |
| 18 |
노드가 하나만 남았으므로 종료한 뒤, 왼쪽 edge를 거치면 0, 오른쪽 edge를 거치면 1로 설정하여 각 알파벳에 대하여 binary code를 설정합니다.
| Binary Code | |
| A | 000 |
| B | 01 |
| C | 001 |
| D | 10 |
| E | 11 |
이를 통해 인코딩을 진행하면 완료됩니다.
🧐 Priority Queue를 통한 구현
위 과정을 빈도수를 우선순위로 가지는 우선순위 큐를 통해 구현할 수 있습니다.
1. 빈도수가 가장 작은 두 알파벳을 선택하기 : deletemin
2. 1에서 선택한 두 alphabet에 해당하는 node를 left와 right로 가지는 tree 생성
3. 1에서 선택한 두 alphabet을 합친 새로운 alphabet을 생성 후 추가 : insert
🧐 수도코드

⭐️ 시간 복잡도
기존 문자열에서 각 alphabet의 빈도수를 측정 : $O(n)$
빈도수 정보를 담은 node 생성하여 Priority queue에 삽입(insert n 번) : $O(n \; log\; n)$
Priority Queue에서 deletemin 2(n-1) 번과 insert n-1 번 : $O(n\;log\;n)$
따라서 총 시간 복잡도는 $O(n\;log\;n)$ 입니다.
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] DP (1) - LIS(최장 증가 부분 수열) (0) | 2022.11.10 |
|---|---|
| [알고리즘] DP (0) - DP 문제를 해결하는 방법 (0) | 2022.11.09 |
| [알고리즘] 그리디 (2) - Interval scheduling (0) | 2022.10.21 |
| [알고리즘] 그리디 (1) - 최소 신장 트리 (Minimum Spanning Tree) (0) | 2022.10.21 |
| [알고리즘] 그리디 (0) -그리디 알고리즘 (0) | 2022.10.13 |