가설 검정 (Hypotheses testing)
어떠한 추측이나 가설에 대하여, 해당 가설의 타당성을 조사하는 것을 가설 검정이라고 합니다.
모수(parameter) $\theta$ 가 알려지지 않은 어떠한 분포를 가정하겠습니다.
그리고 $\Omega $ 를 $\theta$ 에 대한 모수 공간 (paramter space)이라 정의하겠습니다.
$\Omega $ 를 분할(partition)하는 $\Omega_0 $ 과 $\Omega_1 $를 정의하겠습니다.
즉 $\Omega_0 \cap \Omega_1 = \varnothing$ , $\Omega_0 \cup \Omega_1 =\Omega$ 입니다.
위와 같은 상황에서, 통계학자는 실제 모수 $\theta$가 위 두 공간 중 어느 공간에 포함되는지 관심이 있다고 가정하겠습니다.
이를 알아보기 위해서 통계학자는 다음과 같은 가설(hypotheses)을 세웁니다.
모수 $\theta$ 는 $\Omega_0$ 에 존재할거야! $ \to $ $H_0$
모수 $\theta$ 는 $\Omega_1$ 에 존재할거야! $ \to $ $H_1$
위와 같이 가설을 세우고 난 후, 어떤 가설이 참인지를 검정(test) 하여야 합니다.
위와 같이 가능한 결정이 오로지 두 가지뿐인 이러한 유형의 문제를 가설 검정 문제라고 합니다.
이러한 문제에서 잘못된 결정을 내리게 된다면 많은 손해를 볼 수도 있습니다.
가능한 옳은 결정을 내리기 위해 문제를 풀기 전 일부 데이터(표본)를 관찰함으로써 모수에 대한 정보를 얻을 것입니다.
어떤 가설을 선택할지 결정하는 절차를 검정 절차(test procedure) 또는 간단히 검정(test)이라고 합니다.
지금까지의 논의에서 우리는 가설 $H_0$ 과 $H_1$ 을 동등하게 취급했습니다.
그러나 대부분의 문제에서 두 가설은 다르게 취급됩니다.
귀무 가설과 대립 가설 (Null and Alternative Hypotheses)
가설 $H_0$ 를 귀무가설(Null hypotheses) 이라고 하고,
가설 $H_1$ 를 대립가설(Alternative hypotheses) 이라고 합니다.
저희의 목표는 검정을 통하여 귀무가설을 기각(reject)하고,
귀무가설이 기각됨을 통해 대립가설을 채택하는 것입니다.
기각 (reject)
검정을 통해 $\theta$ 가 $\Omega_1$ 에 있다고 결정하면 $H_0$ 을 기각(reject)한다고 합니다.
$\theta$ 가 $\Omega_0$ 에 있다고 결정하면 $H_0$ 을 기각하지 않는다고 합니다.
중요한 것은 $\theta$ 가 $\Omega_0$ 에 있을 때,
$H_1$을 기각하는 것이 아닌
$H_0$을 기각하지 않는다라고 하는 것입니다.
예시
인간의 두개골 폭(Breath) 측정
기원전 4000년 전 두개골의 너비에 대한 측정값은 다음과 같은 정규분포로 모델링합니다. $\sim \;\; N(\mu, \; 26)$
이러한 두개골들이 평균이 약 140mm인 현대 두개골의 너비와 비교하고 싶습니다.
매개변수 공간 $\Omega$ 은 양수이며,
$\Omega_1$ 가 구간 $(0, 140)$인 동안 $\Omega_0$ 은 구간 $[140, \infty)$ 일 수 있습니다.
이 경우 귀무 가설과 대립 가설을 다음과 같이 작성합니다.
$$H_0 \;:\; \mu \geq 140$$
$$H_1 \;:\; \mu < 140$$
단순 가설과 복합 가설 (Simple and Composite Hypotheses)
만약 $\Omega_i \;\;(i \in \left\{ 0,1 \right\})$ 가 오직 하나의 값만을 포함한다면
$\Omega_i$ 는 단순 가설(Simple hypotheses)이라 부릅니다.
그렇지 않은 경우 $\Omega_i$ 는 복합 가설(Composite hypotheses)이라 부릅니다.
예를 들어 $H_0 : \mu =\theta_0 $ 인 경우, $\Omega_0 = \left\{ \theta_0 \right\}$ 이므로, $H_0$ 은 단순 가설입니다.
단측검정과 양측검정 (One-Sided and Two-Sided Hypotheses)
$\theta$ 를 1차원 모수라 하겠습니다.
단측 귀무가설(One-sided null hypotheses)은 다음과 같습니다.
$$H_0 = \theta \leq \theta_0 \;\;\; or \;\;\; \theta \geq \theta_0$$
이에 대응하는 단측 대립가설(One-sided alternative hypotheses)은 다음과 같습니다.
$$H_1 = \theta > \theta_0 \;\;\; or \;\;\; \theta < \theta_0$$
$$H_0 = \theta = \theta_0$$
위와 같이 귀무가설이 단순 가설(simple hypotheses)인 경우,
대응하는 대립가설은 양측(Two-sided) 가설입니다.
위 경우에는 대립 가설이 다음과 같습니다.
$$H_1 = \theta \neq \theta_0$$
Critical Region과 검정통계량(Test statistic)
다음과 같은 예시를 들며 시작하겠습니다.
알려지지 않은 평균 $\mu$ 와, 알려진 분산 $\sigma^{2}$ 을 가지는 정규분포 $N(\mu, \sigma^{2})$ 에서 임의추출한 n개의 표본 $X = (X_1, X_2, ..., X_n)$ 이 있습니다.
저희는 다음과 같은 가설을 검정하고 싶습니다.
$$H_0 : \mu = \mu_0$$
$$H_1 : \mu \neq \mu_0$$
(이때 $\mu_0$ 를 hypothesized value라 부릅니다.)
$H_0 : \mu = \mu_0$이므로, 만약 $\overline{X}_n$ 가 $\mu_0$ 에서 멀리 떨어진 값이라면, $H_0$ 을 기각하는 것이 합리적입니다.
예를 들어 임의의 숫자 c를 하나 지정하겠습니다.
그리고 만약 $\overline{X}_n$ 가 $\mu_0$ 에서 c 이상 떨어져있다면 이를 기각할 수 있습니다.
한 가지 방법은 가능한 모든 데이터 $x = (x1,...,xn)$ 의 집합 $S$ (Sample Space)를 다음 두 집합으로 나누는 것입니다.
$$S_0 = \left\{ x : -c \leq \overline{X}_n - \mu_0 \leq c \right\}$$
$$S_1 = S_0^{C}$$
그리고 $X \in S_1$ 인 경우 귀무가설 $H_0$ 를 기각합니다.
이를 표현하는 더 간단한 방법은, 통계량(statistic) T를 $T = | \overline{X}_n - \mu_0|$ 라 정의한 후, $T > c$ 인 경우 $H_0$ 를 기각하는 것입니다.
위의 예시에서 $S_1$ 을 검정에서의 critical region이라 부릅니다.
요약
검정 절차는 검정의 critical region을 지정하고
관측된 데이터들의 통계량 $T = r(X)$ 이 $S_1$ 에 속할 때 $H_0$ 을 기각하는 과정을 따릅니다.
검정 통계량(test statistic)
통계량(statistic) - 모집단에서 추출한 표본을 이용하여 구할 수 있는 모든 값
검정에서 사용되는 통계량을 검정 통계량(test statistic)이라 부릅니다.
X를 모수 $\theta$ 에 의존하는 분포에서 임의추출한 표본이라 하겠습니다.
$T=r(X)$ 를 통계량(statistic)이라 정의하고, $R$ 을 실수의 부분집합이라고 하겠습니다.
검정 절차가 '$T \in R$인 경우 $H_0$ 을 기각' 하는 형식이라고 가정합니다.
하나의 보편적인 예시로는' $T \geq c$ 일 때 $H_0$ 을 기각 ' 의 형식이 있으며, 앞으로 자주 등장합니다.
이러한 경우 $T$ 를 검정 통계량이라 부릅니다.
기각역 (Rejection Region)
위의 부분에서 $R$ 을 검정의 기각역(rejection region)이라 부릅니다.
검정이 위에서와 같이 검정 통계량 $T$ 와 기각역(rejection region)$R$ 의 관점에서 정의될 때,
집합 $S_1 = \left\{ (x_1,..., x_n) : T \in R \right\}$는 critical region입니다.
일반적으로 검정 통계량 T에 기반한 검정의 기각역(rejection region)은 고정된 간격이거나, 고정된 간격 이외의 부분입니다.
예를 들어, 만약 검정에서 $T \geq c$ 일 때 $H_0$ 를 기각한다고 하면, 기각역(rejection region)은 구간 $[c, \infty )$ 입니다.
이러한 경우 테스트는 다음과 같은 절차를 따릅니다.
일단 검정 통계량이 사용되면, critical region을 계산하는 것 보다, 검정 통계량의 관점에서 모든 것을 표현하는 것이 훨씬 간단합니다.
이제부터 나머지 부분의 모든 테스트는 검정 통계량을 기반으로 합니다.
실제로 대부분의 테스트는 "$T \geq c$인 경우 $H_0$ 기각" 형식으로 작성할 수 있습니다.
$$S_1 = \left\{ (x_1, ..., x_n) \;:\; T \in R \right\}$$
$S_1$ : critical region
$T$ : 검정 통계량(test statistic)
$R$ : 기각역(rejection region)
Power function (검정력 함수)
검정력 함수 $\pi (\theta | \delta)$ 는, 모수 $\theta$ 의 가능한 각 값에 대하여
$\delta$ (테스트)가 귀무가설( $H_0$) 을 기각할 확률을 나타냅니다.
'검정력(Power)이 강하다'는 '귀무가설을 잘 기각시킨다',
'검정력(Power)이 약하다'는 '귀무가설을 잘 기각시키지 못한다'의 의미입니다.
기각역이 커지면 기각할 확률이 높아지고, 기각역이 작아지면 확률이 낮아집니다.
기각할 확률이 높아진다는 것은 검정력 함수 $\pi (\theta | \delta)$ 의 값이 높음을,
기각할 확률이 낮아진다는 것은 검정력 함수 $\pi (\theta | \delta)$ 의 값이 낮음을 의미합니다.
다음과 같이 정의됩니다.
$\delta $ : test (procedure)
$ S_1 $ : $\delta$ 에서의 critical region
$R$ : $\delta$ 에서의 기각역(rejection region)
$T$ : 검정통계량(test Statistic)
위와 같은 상황에서, 검정 $\delta$ 에 대한 power function $\pi(\theta \;|\; \delta)$ 는 다음과 같습니다.
$$\pi (\theta | \delta) = P(X \in S_1 | \theta) $$
$\delta$ 가 검정 통계량 T 및 rejection region으로 설명되는 경우에는 다음과 같이 표현합니다.
$$\pi (\theta | \delta) = P(T \in R | \theta) $$
검정력 함수(Power function)의 결과는 확률입니다.
이상적인 검정력 함수는
$\theta \in \Omega_0$ 인 $\theta$ 에 대해 $\pi (\theta | \delta) = 0 $ 이고,
$\theta \in \Omega_1$ 인 모든 $\theta$ 에 대해 $\pi (\theta | \delta) = 1 $ 일 것입니다.
예시
정규분포를 따르며 분산이 알려진 집단에서의 평균에 대한 가설 검정
대상이 되는 집단이 $N(\mu, \sigma^2)$ 을 따르며, 이때 분산은 알려져 있다고 합니다.
표본평균은 모집단이 $N(\mu, \sigma^2)$ 이므로 다음과 같은 정규분포를 따릅니다.
$$\overline{X}_n \; \sim \; N(\mu, \frac{\sigma^{2}}{n})$$
귀무가설($H_0$ )과 대립가설($H_1$ ), 검정통계량($T$ )과 rejection region($R$ )이 다음과 같을 때
$$H_0 = \mu =\mu_0$$
$$H_1 = \mu \neq \mu_0$$
$$T = |\overline{X}_n - \mu_0|$$
$$R = (c, \infty)$$
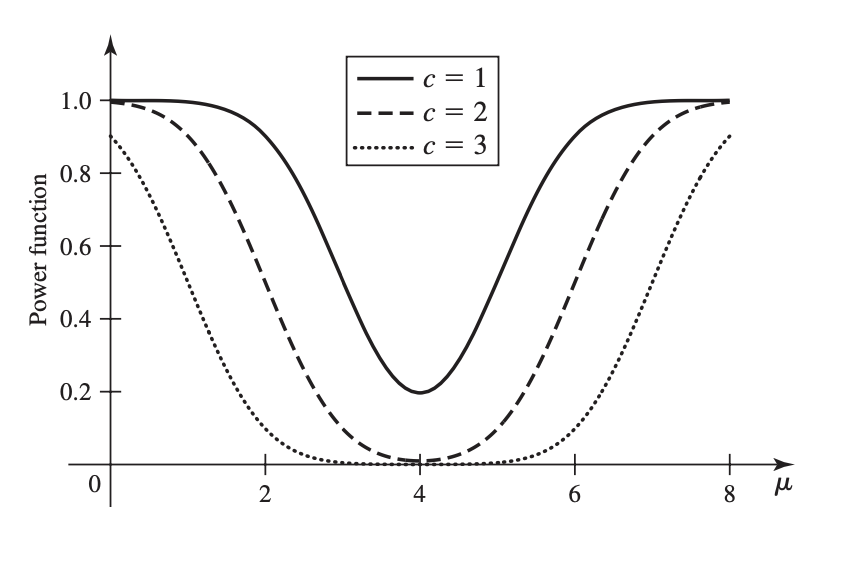
검정력 함수(power functiom)는 다음과 같습니다.
$$\pi(\mu \;|\; \delta) = P(T \in R \; | \; \mu) = P(\overline{X}_n -\mu_0 > c) + P(\overline{X}_n -\mu_0 < -c) $$
$$=P(\frac{\overline{X}_n - \mu}{\frac{\sigma}{\sqrt{n}}} > \frac{\mu_0 + c - \mu}{\frac{\sigma}{\sqrt{n}}} )$$
$$+P(\frac{\overline{X}_n - \mu}{\frac{\sigma}{\sqrt{n}}} < \frac{\mu_0 - c - \mu}{\frac{\sigma}{\sqrt{n}}} )$$
$$= 1 - \Phi(\frac{\mu_0 + c - \mu}{\frac{\sigma}{\sqrt{n}}}) + \Phi(\frac{\mu_0 - c - \mu}{\frac{\sigma}{\sqrt{n}}})$$
1종 오류와 2종 오류 (Type I / II Error)
1종 오류 (Type I Error) : 옳은 귀무가설을 기각하는 오류입니다.
2종 오류 (Type II Error) : 틀린 귀무가설을 기각하지 않는 오류입니다.
검정력 함수(Power function)의 관점에서, 1종 오류를 범할 확률은 다음과 같습니다.
$$\pi(\theta | \delta) \;\;\; if\; \theta \in \Omega_0$$
($\theta \in \Omega_0 \; \to $ 귀무가설( $H_0$ )이 참인 경우에, $\pi(\theta | \delta) \; \to $ 귀무가설을 기각할 확률)
또한 2종 오류를 범할 확률은 다음과 같습니다.
$$1 - \pi(\theta | \delta) \;\;\; if\; \theta \in \Omega_1$$
($\theta \in \Omega_1 \; \to $ 귀무가설( $H_1$ )이 거짓인 경우에, $1 - \pi(\theta | \delta) \; \to $ 귀무가설을 기각하지 않을 확률)
진짜 미치지 않고서야 가능하다면 오류를 범할 확률이 적은 검정을 선택하고 싶을 것입니다.
즉 $\theta \in \Omega_0$에 대하여, 검정력 함수($\pi(\theta | \delta)$)의 값이 낮으며,
$\theta \in \Omega_1$에 대하여, 검정력 함수($\pi(\theta | \delta)$)의 값이 높기를 원합니다.
그러나 이는 불가능합니다.
$\theta \in \Omega_0$에 대한 검정력 함수($\pi(\theta | \delta)$)의 값이 낮은 검정을 선택하면
$\theta \in \Omega_1$에 대한 검정력 함수($\pi(\theta | \delta)$)의 값도 낮아집니다.
1종 오류를 범할 확률이 낮아지면, 2종 오류를 범할 확률이 높아집니다.
역도 성립합니다.
예를 들어
$$\pi (\theta | \delta) = 0 \;\;\;\; \forall \theta \in \Omega_0 \; \to \pi (\theta | \delta) = 0 \;\;\;\; \forall \theta \in \Omega_1 $$
(귀무가설이 참일 때 이를 기각할 확률이 0이라면,
귀무가설이 거짓일 때 이를 기각할 확률이 0, 즉 기각하지 않을 확률이 1입니다.)
또한 다음도 성립합니다.
$$\pi (\theta | \delta) = 1 \;\;\;\; \forall \theta \in \Omega_1 \; \to \pi (\theta | \delta) = 1 \;\;\;\; \forall \theta \in \Omega_0 $$
(귀무가설이 거짓일 때 이를 기각할 확률이 1이라면,
귀무가설이 참일 때 이를 기각할 확률이 1입니다.)
따라서 1종 오류과 2종 오류를 범할 확률 사이에서 균형을 맞추는 것이 중요하며,
대부분의 경우 1종 오류를 범할 최대 확률(Upper Bound)을 제어하여 결정합니다.
즉 다음과 같습니다.
0과 1 사이의 숫자 $\alpha_0$ 를 1종 오류를 범할 최대 확률로 결정합니다.
$$\pi(\theta| \delta) \leq \alpha_0, \;\;\;\;\; \forall \theta \in \Omega_0$$
이후 귀무가설 $H_0$ 를 기각했다면, 귀무가설이 틀린 것이므로 대립가설이 맞다고 주장할 수 있습니다.
귀무가설과 대립가설의 선택
우리가 가설을 세울 때, 귀무가설은 우리가 주장하고 싶은 주장과 반대되게 세워야 합니다.
그리고 귀무가설이 기각되었다면, 우리의 주장이 옳다고 주장할 수 있게 됩니다.
예시
두개골의 폭
현대인의 두개골의 폭의 평균 : 140
기존의 주장 : 두개골의 폭은 오랜 기간 동안 증가되어왔을 것이다.
나의 주장 : 아니
위와 같은 상황에서, 기원전 3000년 경의 두개골의 폭을 $N(\mu, 26)$으로 모델링할 수 있을 때, 귀무가설( $H_0$ )과 대립가설( $H_1$ )은 다음과 같습니다.
$$H_0 : \mu \geq 140$$
$$H_1 : \mu <140$$
유의수준 (Significance Level)
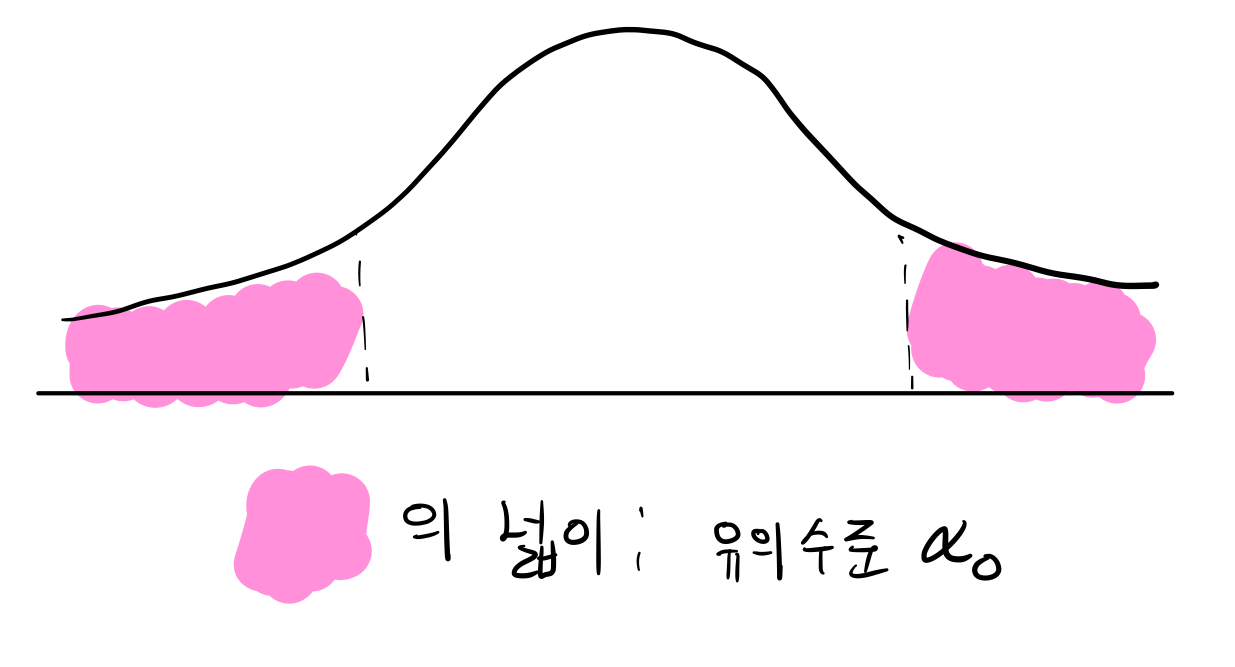
귀무가설을 기각하는 확률을 유의수준이라고 부릅니다.
검정( $\delta$ )이 귀무가설을 기각할 최대 확률이 $\alpha_0$ 라 하겠습니다. 즉 다음과 같습니다.
$$\pi(\theta | \delta) \leq \alpha_0$$
위와 같은 경우에 검정( $\delta $ )를 level-$\alpha_0$ 검정이라고 하며,
검정의 유의 수준(Significance Level)이 $\alpha_0$ 라고 합니다.
검정의 크기(size)는 $\Omega_0$ 에 존재하는 $\theta$ 에 대하여(즉 귀무가설이 옳은 경우),
귀무가설을 기각할 확률의 상한(UpperBound)(즉, 1종 오류를 범할 확률)으로 정의됩니다.
즉 위의 경우 검정의 크기 $\alpha (\delta)$ 는 다음과 같습니다.
$$ \alpha (\delta) = sup_{\theta \in \Omega_o}\pi (\theta | \delta)$$
(sup X는 X 이상의 값들 중 최솟값을 의미합니다.)
정의에 따라 다음이 성립합니다.
1. 만약 검정 $\delta$가 level-$\alpha_0$ 검정이라면, 검정의 크기 $\alpha(\delta)$ 는 최대 $\alpha_0$ 입니다.
2. 만약 귀무가설 $H_0$ 가 단순(Simple) 가설, 즉 $H_0 : \theta = \theta_0$ 라면,
검정 $\delta$의 크기는 $\alpha(\delta) = \pi(\theta_0 | \delta)$ 입니다.
특정 유의 수준을 갖는 테스트 만들기
다음과 같은 가설에 대한 검정을 진행하고 싶다고 가정하겠습니다,.
$$H_0 : \theta \in \Omega_0$$
$$H_1 : \theta \in \Omega_1$$
T를 검정 통계량(test statistic)이라 정의한 후, $T \geq c$ 인 경우에 귀무가설 $H_0$ 를 기각한다고 하겠습니다.
그리고 유의수준(significance level)을 $\alpha_0$ 라 정하고 싶은 욕구가 있다고 하겠습니다.
유의수준은 귀무가설을 기각할 최대 확률이므로,
귀무가설을 기각할 확률을 나타내는 검정력 함수 $\pi (\theta | \delta)$의 최댓값을 $\alpha_0$ 로 정하는 것을 원하는 것입니다.
$$sup_{\theta \in \Omega_0}P(T \geq c | \theta) \leq \alpha_0$$
위에서 왼쪽 부분은 c에 대하여 감소하는 함수입니다.
즉 c가 커진다면 확률은 0이 될 것이므로 위 식은 항상 성립하지만,
$\theta \in 1$ 에 대하여 검정력 함수(귀무가설을 기각할 확률)를 최대한 크게 하려면, c를 가능한 작게 만들어야 합니다.
정규분포를 따르며 분산이 알려진 집단에서의 평균에 대한 가설 검정
대상이 되는 집단이 $N(\mu, \sigma^2)$ 을 따르며, 이때 분산은 알려져 있다고 합니다.
가설은 다음과 같습니다.
$$H_0 : \mu = \mu_0$$
$$H_1 : \mu \neq \mu_0$$
검정 통계량(Test statistic)은 다음과 같습니다.
$$T = |\overline{X}_n - \mu_0|$$
$T > c$ 인 경우 $H_0$ 를 기각한다고 하겠습니다.
즉 다음과 같습니다.
$$\pi(\theta | \delta) = P(T \geq c | \delta)$$
유의수준(significance level)을 $\alpha_0$ 로 정하려 합니다. 즉 다음과 같습니다.
$$sup_{\theta \in \Omega_0} P(T > c| \theta) = P(|\overline{X}_n - \mu_0| > c | \mu_0) \leq \alpha_0$$
이제 c를 정해보겠습니다.
모집단이 $N(\mu, \sigma^2)$ 를 따르기 때문에, 표본평균은 다음과 같은 분포를 따릅니다.
$$N(\mu, \frac{\sigma^2}{n})$$
확률변수 $Y$ 를 다음과 같이 정의하겠습니다.
$$Y = \overline{X}_n - \mu_0 $$
이때 만약 귀무가설에서 주장하는 바와 같이 $\mu = \mu_0$라면 $Y$ 는 다음 정규분포를 따릅니다.
$$N(0, \frac{\sigma^2}{n})$$
$$P(|\overline{X}_n - \mu_0| > c\; | \;\mu_0) \leq \alpha_0$$
위의 식을 정규화하면 아래과 같습니다.
$$P(|Z| \geq \frac{c}{\frac{\sigma}{\sqrt{n}}} \;| \;\mu_0) \leq \alpha_0$$
이것은 아래를 의미합니다.
$$2(1-\Phi(\frac{c}{\frac{\sigma}{\sqrt{n}}})) = \alpha_0$$
위 식을 $\Phi(\frac{c}{\frac{\sigma}{\sqrt{n}}})$ 에 대하여 나타내면 아래과 같습니다.
$$\Phi(\frac{c}{\frac{\sigma}{\sqrt{n}}}) = 1-\frac{\alpha_0}{2}$$
c에 대해 정리하겠습니다.
$$\Phi(\frac{c}{\frac{\sigma}{\sqrt{n}}}) = 1-\frac{\alpha_0}{2}$$
$$\frac{c}{\frac{\sigma}{\sqrt{n}}} = \Phi^{-1}(1- \frac{\alpha_0}{2})$$
$$c = \Phi^{-1}(1- \frac{\alpha_0}{2}) \cdot \frac{\sigma}{\sqrt{n}}$$
정규 분포에 대한 가설 검정을 진행하는 경우, 이를 검정통계량의 관점에서 다시 작성하는 것이 일반적입니다.
즉 검정통계량을 다음과 같이 설정한 후
$$|Z| = \frac{\overline{X}_n - \mu_0}{\frac{\sigma}{\sqrt{n}}}$$
위에서 구한 c를 사용하여 다음과 같이 표현할 수 있습니다.
$$P(|Z| > \Phi^{-1}(1- \frac{\alpha_0}{2})) \leq \alpha_0$$
즉 테스트의 절차를
$|Z| \geq c$ 인 경우 $H_0$ 을 기각하는 것으로 다시 작성하는 것입니다.
그리고 c는 유의수준 $\alpha_0$에 의해 정해집니다.
참고 - 검정통계량의 관점?
통계량은 표본으로 구할 수 있는 모든 것들을 의미하므로, $|Z|$ 역시 통계량입니다.
그리고 검정 절차에서 사용되는 통계량을 검정 통계량이라 부릅니다.
유의확률 (P-value)
level -0.05 검정을 가정하겠습니다.
level -0.05 검정은 위에서 확인했던 것 처럼 $|Z| \geq \Phi^{-1}(1 - \frac{0.05}{2})$인 경우 $H_0$ 을 기각합니다.
이때 $|Z|$ 는 표본을 관찰하여 얻어진 값이므로 항상 고정된 값을 가집니다.
$|Z| = 1.97$ 인 경우 $\alpha_0=0.05$인 검정에서는 $H_0$ 을 기각합니다.
그러나 $\alpha_0=0.01$인 검정에서는 $H_0$ 을 기각하지 않습니다.
만약 $|Z| = 2.78$ 인 경우는 어떨까요?
이미 관찰된 데이터에 대하여, level-$\alpha_0$ 검정에서 $H_0$ 이 기각되게 하는 최소의 $\alpha_0$를 의미합니다.
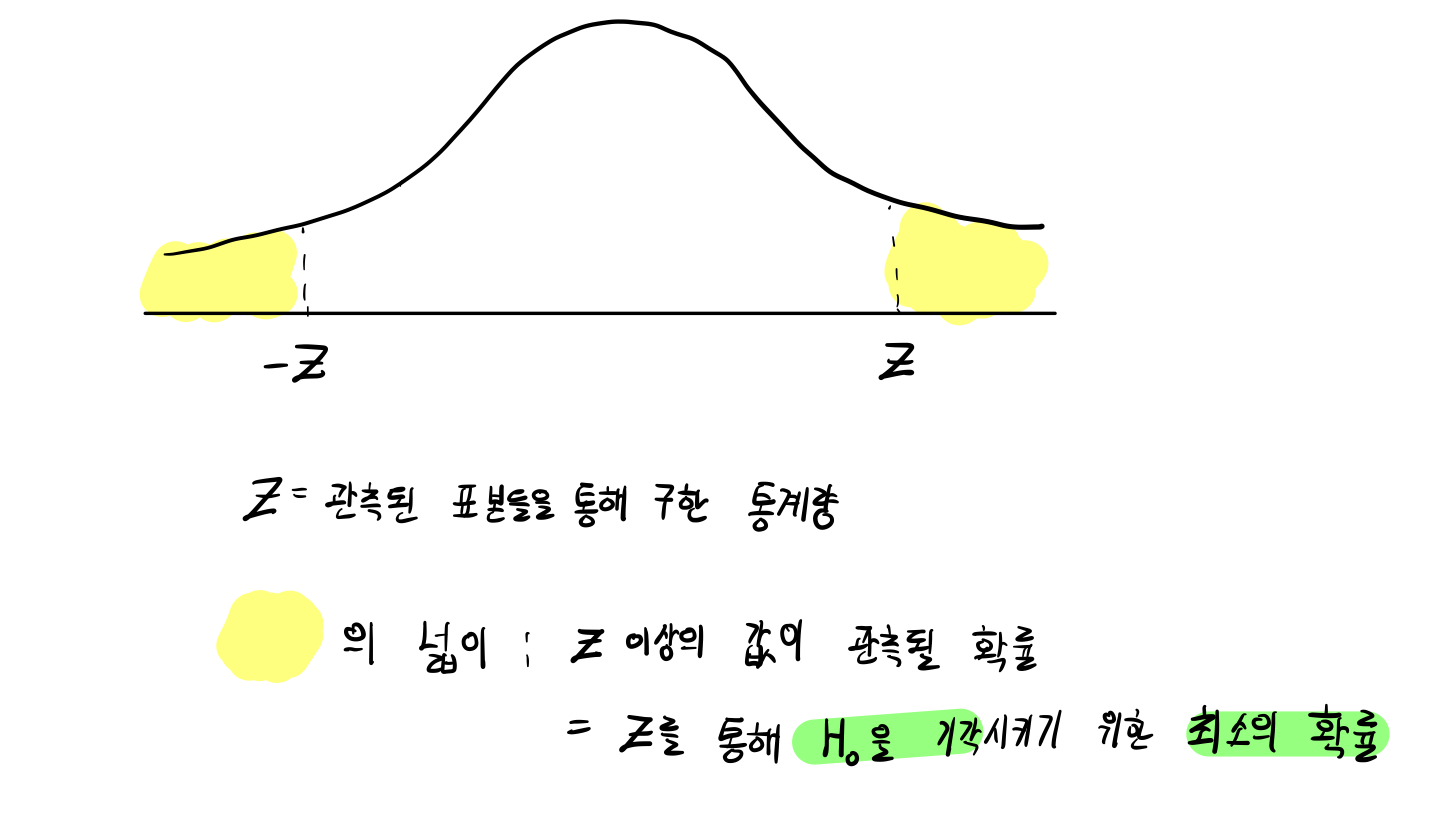
유의수준이 $\alpha_0$라는 것은 검정( $\delta$ )이 $H_0$ 을 기각할 최대 확률이 $\alpha_0$이라는 것이며,
P-value는 $H_0$ 을 기각할 최대 확률이 $\alpha_0$ 인 검정에서, 이미 관측된 데이터로 인해 $H_0$이 기각되는 최소의 $\alpha_0$ 를 의미합니다.
쉽게 말하면 관측된 데이터로 $H_0$ 가 기각되는 최소 확률 입니다.
귀무가설이 기각되는 조건
$$p-value < a_0$$
이때 $a_0$ 는 유의수준(significance level)
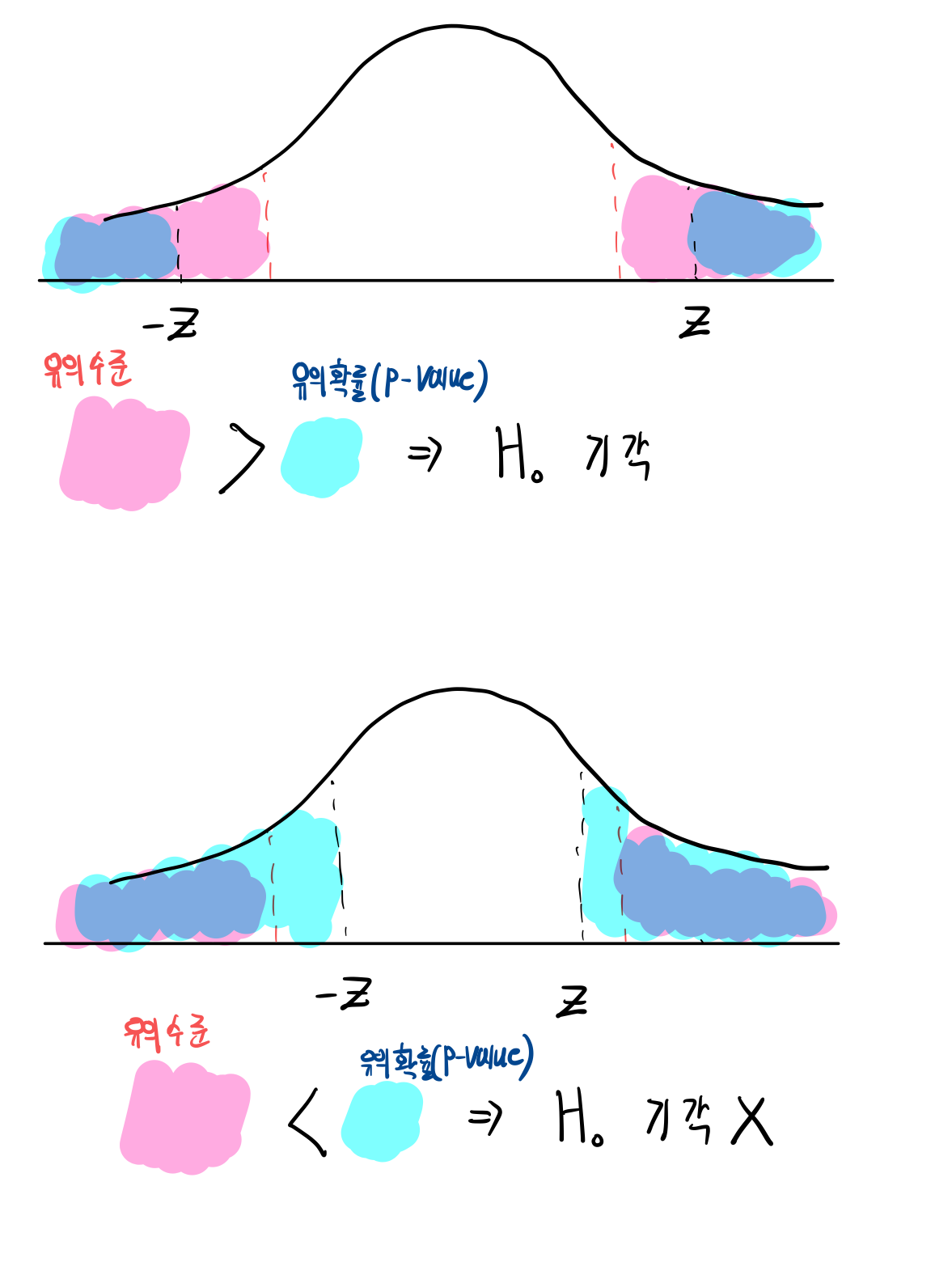
예를 들어 p-value가 0.1인 경우에 $a_0 = 0.11$ 이라면, 이는 p-value보다 크므로 $H_0$ 을 기각시킵니다.
그러나 $a_0 = 0.01$ 이라면, 이는 p-value보다 작으므로 $H_0$ 을 기각시키지 않습니다.
다시 이전 예시로 돌아가서 $|Z| = 2.78$ 인 경우에는 어떻게 될지 확인해 보겠습니다.
명심해야 할 것은, $|Z|$ 는 이미 표본을 통해 관찰된 통계량이라는 것입니다.
$H_0$ 을 기각하기 위해서는 $|Z| \geq 2.78$ 이어야 합니다.
$P(|Z| \geq c) \leq \alpha_0$ 의 식이 기억나시나요?
이때 p-value는 $P(|Z| \geq c) = \alpha_0$ 인 $ \alpha_0 $ 이므로
$$P(|Z| \geq 2.78) = 0.0054$$
(0.0054는 테이블을 참조해서 구했습니다.)
즉 p-value는 0.0054이며,
따라서 유의수준 $\alpha_0$ 가 0.01인 검정에서는 $H_0$ 을 기각하지만,
따라서 유의수준 $\alpha_0$ 가 0.0000000001인 검정에서는 $H_0$ 을 기각하지 않습니다.
T=t로 관찰되었을 때, p-value는 검정 $\delta $ 의 크기입니다.
$$p-value = sup_{\theta \in \Omega_0}\pi(\theta | \delta) = sup_{\theta \in \Omega_0}P(T \geq t | \theta) $$
'🖥 Computer Science > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] - (24) 가설 검정[0] - 가설검정 이해하기 (2) | 2022.06.07 |
|---|---|
| [확률과 통계] - (23) 불편추정량 (Unbiased estimator) (feat. 표본분산을 n-1로 나누는 이유) (0) | 2022.06.01 |
| [확률과 통계] - (22) 신뢰구간(Confidence Intervals) (0) | 2022.05.31 |
| [확률과 통계] - (21) t 분포 (스튜던트 t 분포) (t Distribution) (0) | 2022.05.24 |
| [확률과 통계] - (20) 표본 평균과 표본 분산의 결합분포 (2) | 2022.05.24 |