(스튜던트) T 분포 (Student t-distribution)
이전에 배웠던 카이제곱 분포는 표본들의 통계량을 통해서, 모집단의 분산을 추정하는데 사용되었습니다.
그러면 모집단의 평균은 무엇으로 추정할 수 있을까요?
이번에 배울 T분포를 통해 모집단의 평균을 추정할 수 있습니다.
T분포는 스튜던트 T 분포, 학생 T 분포 등으로 불리며,
표본분산을 이용하여 정규분포를 따르는 모집단의 평균을 추정할 때 주로 사용되는 분포입니다.
모평균에 대한 신뢰구간이나 가설검정에서 사용됩니다.
T 분포의 정의
두개의 독립인 확률변수 Y , Z를 다음과 같이 정의할 때,
$$Y\; \sim \; \chi^{2}(m)$$
$$Z \; \sim \; N(0, 1^{2})$$
확률변수 X를 다음과 같이 정의하면
$$X = \frac{Z}{(\frac{Y}{m})^{\frac{1}{2}}}$$
이때 X는 자유도 m을 가진 t-distribution을 따른다고 하며, 다음과 같이 나타냅니다.
$$X \; \sim \; T(m)$$
T 분포의 p.d.f
x의 범위는 $-\infty$ 부터 $\infty$ 입니다.
$$f(x\;|\;m) = \frac{\Gamma(\frac{m+1}{2})}{(m\pi)^{\frac{1}{2}} \Gamma(\frac{m}{2})}(1+\frac{x^{2}}{m})^{\frac{-(m+1)}{2}} $$
T 분포의 형태
정규분포와 마찬가지로 대칭(Symmetric)인데, 이때 x=0에 대하여 대칭입니다.
자유도가 커질수록 표준정규분포에 가까워집니다.
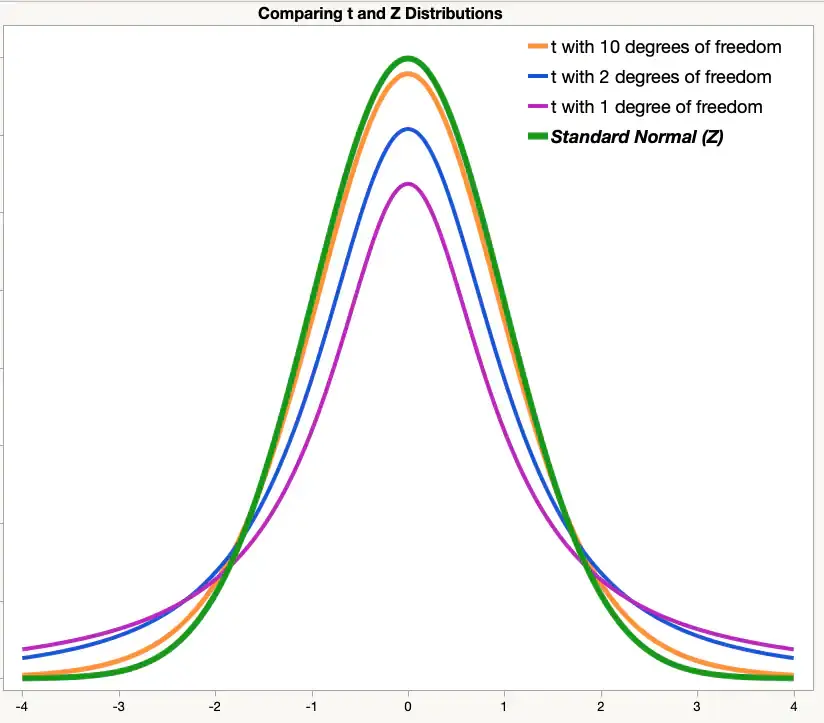
T 분포의 속성
평균
확률변수 X가 자유도 m인 t 분포를 따를 때 평균은 다음과 같습니다.
$$E(X) = \infty \;\;\;\;\;\;\; m \leq 1$$
$$E(X) = 0 \;\;\;\;\;\;\; m > 1$$
분산
확률변수 X가 자유도 m인 t 분포를 따를 때 분산은 다음과 같습니다.
$$Var(X) = \frac{m}{m-2} \;\;\;\;\;\;\; m > 2$$
m.g.f
m.g.f가 존재하기 위해서는 다음을 만족해야 합니다.
$$E(|X|^{k}) < \infty$$
이때 k는 항상 1 이상이지만, m이 1보다 작은 경우 평균이 무한대로 발산하므로, 위 식을 만족하지 않으며, 따라서 m.g.f는 존재하지 않습니다.
정규분포의 표본과의 관계
정규분포 N($\mu$ ,$\sigma^2$)를 따르는 모집단으로부터 추출한 n개의 표본 $X_1$, ..., $X_n$에 대하여,
$\sigma$' 을 다음과 같이 정의합니다.
$$\sigma' = \begin{bmatrix} \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}}{n-1} \end{bmatrix}^{\frac{1}{2}}$$
이때 다음이 성립합니다.
$$\frac{\overline{X}_n - \mu}{\frac{\sigma'}{\sqrt{n}}} \;\sim\;T(n-1)$$
증명
다음과 같이 정의하겠습니다.
$$S^{2}_n = \sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}$$
$$Z = \frac{\overline{X}_n - \mu}{\frac{\sigma}{\sqrt{n}}} \;\; \sim \; N(0, \;1)$$
$$Y = \frac{S^{2}_n}{\sigma^{2}}\;\;\sim\; \chi^{2}(n-1)$$
이때 이전에 배웠듯이 Z와 Y는 독립입니다.
또한 Y가 자유도 n-1인 카이제곱 분포를 따르는 이유는 다음과 같습니다.
$$Y = \frac{S^{2}_n}{\sigma^{2}} = \frac{ \sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}}{\sigma^{2}} \; \sim \; \chi^{2}(n-1)$$
이제 U를 다음과 같이 정의하면, t 분포의 정의에 따라, U는 자유도 n-1을 가지는 t 분포를 따릅니다.
$$U = \frac{Z}{(\frac{Y}{n-1})^{\frac{1}{2}}}\;\sim \;T(n-1)$$
또한 U를 다음과 같이 쓸 수 있습니다.
$$U = \frac{\frac{\overline{X}_n-\mu}{\frac{\sigma}{\sqrt{n}}}}{(\frac{S_n^{2}}{\sigma^{2}(n-1)})^{\frac{1}{2}}}$$
이때 분모와 분자의 $\sigma$는 약분되어 다음과 같아집니다.
$$U = \frac{ \sqrt{n}(\overline{X}_n-\mu) }{(\frac{S_n^{2}}{(n-1)})^{\frac{1}{2}}}$$
이때 분모는 $\sigma$' 과 같습니다. 즉 다음의 식이 도출됩니다.
$$U = \frac{ \sqrt{n}(\overline{X}_n-\mu) }{\sigma '} \;\;\;\;\; \because \sigma' = \begin{bmatrix} \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}}{n-1} \end{bmatrix}^{\frac{1}{2}}$$
즉 다음이 증명됩니다.
$$\frac{\overline{X}_n - \mu}{\frac{\sigma'}{\sqrt{n}}} \;\sim\;T(n-1)$$
위의 증명에서 중요한 부분이 있으며, 다음과 같습니다.
1. U의 값 혹은 U의 분포가 모분산 $\sigma$에 의존하지 않습니다.
2. 다음과 같은 정규화된 확률변수 Z에서 $\sigma$(모분산)를 $\sigma$'로 교체하면 U와 같아지며,
따라서 Z의 분포는 SND에서 자유도가 n-1인 t 분포로 바뀝니다.
$$Z = \frac{(\overline{X}_n-\mu)}{\frac{\sigma}{\sqrt{n}}} \; \sim \; N(0, 1^{2})$$
$$\frac{\overline{X}_n - \mu}{\frac{\sigma'}{\sqrt{n}}} \;\sim\;T(n-1)$$
(t 분포는 매우 큰 n에 대하여 SND와 비슷합니다.)
이때 위에서 알아본 것과 같이 U는 σ를 포함하지 않으며, 또한 따라서 σ에 의존적이지 않은 분포를 따릅니다.
따라서 t 분포는 모분산을 모를 때, 모평균을 추정하기 위해 사용이 가능합니다.
모평균을 추정하는 방법은 이후 신뢰구간을 다룰 때 언급하도록 하겠습니다.
$\sigma$'과 $\sigma$에 대한 M.L.E인 $\sigma$^은 각각 다음과 같으며,
$$\sigma '^{2} = \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2} }{n-1}$$
$$\hat{\sigma }^{2} = \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2} }{n}$$
둘 사이에는 다음 관계가 성립합니다.
$$σ'^{2} = (\frac{n}{n-1})\hat{\sigma^{2}}$$
T 분포와 SND
위에서 살펴보았으나 중요하기에 정리하고 넘어가겠습니다.
정규분포를 따르는 확률변수를 정규화할 때,
$\sigma$(모분산) 대신 $\sigma$'을 사용하여 정규화한다면 U와 같아지며,
따라서 정규화된 분포는 SND에서 자유도가 n-1인 t 분포로 바뀝니다.
$$Z = \frac{(\overline{X}_n-\mu)}{\frac{\sigma}{\sqrt{n}}} \; \sim \; N(0, 1^{2})$$
$$\frac{\overline{X}_n - \mu}{\frac{\sigma'}{\sqrt{n}}} \;\sim\;T(n-1)$$
또한 T분포표를 보면 알 수 있듯이 만약 n이 커진다면, σ'는 σ에 가까워집니다.
따라서 Z에서 σ를 σ'로 교체하는 것은 Z의 분포에 큰 영향을 미치지 않습니다.
이러한 이유로 자유도가 n-1인 t 분포는 n이 커질수록 SND에 근접합니다.
$\sigma$'이 먼가용?
이후 불편추정량 부분에서 다시 언급하겠으나, 이해를 돕기 위해 언급하겠습니다.
위에서 정의된 $\sigma$'은 표본분산이며, 실제 분산에 대한 불편추정량입니다.
이전에 평균과 분산을 둘 다 모를 때, 모분산 $\sigma$에 대한 M.L.E 는 $\sigma$^으로 표기하며, 이는 일반적인 분산의 정의에 따른 '편차제곱의 합의 평균'과 동일하며, 다음과 같았습니다.
$$\hat{\sigma}^{2} = \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}}{n} $$
그러나 위에서 정의된 표본분산을 불편추정량으로 만들기 위해서 표본분산을 구할 때 n 대신 n-1로 나눕니다.
추정량의 기댓값이 모수와 같아질 때, 해당 추정량을 불편추정량이라 부릅니다.
Reference
https://m.blog.naver.com/mykepzzang/220853827288
[확률과 통계] 50. t 분포, Student's t-Distribution
이번에 다룰 주제는 '스튜던트 t 분포(Student's t-Distribution)'입니다. 간단하게 't-분포'라고 많이 ...
blog.naver.com
8.5 스튜던트 t분포, 카이제곱분포, F분포 — 데이터 사이언스 스쿨
.ipynb .pdf to have style consistency -->
datascienceschool.net
https://1992jhlee.tistory.com/19
불편추정량(Unbiased Estimate) - 표본분산은 왜 n-1로 나누나?
통계를 공부하다 보니 굉장히 불편한 것을 하나 만나게 됐다. 그것은 바로 표본에서 분산을 정의할 때 원래 알던 분산의 정의(편차의 제곱의 평균)가 아닌 다른 방식으로 정의한다는 것이다.
1992jhlee.tistory.com
https://hsm-edu.tistory.com/13
[손으로 푸는 통계 ver1.0] 2. 자유도와 불편추정량 (왜 n-1로 나누나요?)
[통계 기초] 2. 자유도와 불편추정량 (왜 n-1로 나누나요?) 지난시간에 배운 분산 수식은 아래와 같습니다. $\begin{align}V(X)&=E\left [ \left ( X-\mu \right )^2 \right ]\\&=\frac{\..
hsm-edu.tistory.com
https://ko.wikipedia.org/wiki/%EB%B6%88%ED%8E%B8_%EC%B6%94%EC%A0%95%EB%9F%89
불편 추정량 - 위키백과, 우리 모두의 백과사전
추정량의 기대값이 모수와 같아진다면, 이 추정량을 불편추정량이라 한다. 표본평균의 기대값은 모평균과 같으므로 불편추정량이다. 표본분산의 기대값은 모분산과 다르므로 불편추정량이 아
ko.wikipedia.org
https://kongdols-room.tistory.com/152
신뢰구간추정(스튜던트 t-분포, 표준정규분포)-확률과통계(21)
신뢰구간추정(t-분포, 표준정규분포) 본 포스팅에서는 신뢰구간에 대한 설명(Confidence interval)과 스튜던트 t-분포(Student's t-distribution), 표준정규분포(Standard Normal Distribution)을 사용하여 신뢰..
kongdols-room.tistory.com
https://soooprmx.com/%EB%AA%A8%ED%8F%89%EA%B7%A0%EC%9D%98-%EC%B6%94%EC%A0%95/
모평균의 추정 · Wireframe
중심극한 정리에 따르면 모집단의 데이터의 분포에 무관하게, 표본의 크기가 충분히 크다면 표본 평균의 분포는 그 평균의 모평균과 같고, 분산이 모분산을 표본수로 나눈 값인 정규분포에 가
soooprmx.com
'🖥 Computer Science > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] - (23) 불편추정량 (Unbiased estimator) (feat. 표본분산을 n-1로 나누는 이유) (0) | 2022.06.01 |
|---|---|
| [확률과 통계] - (22) 신뢰구간(Confidence Intervals) (0) | 2022.05.31 |
| [확률과 통계] - (20) 표본 평균과 표본 분산의 결합분포 (2) | 2022.05.24 |
| [확률과 통계] - (19) 카이제곱 분포 (Chi-Square Distribution) (3) | 2022.05.23 |
| [확률과 통계] - (18) 통계량(statistic)과 표본분포(Sampling Distribution) (0) | 2022.05.23 |
(스튜던트) T 분포 (Student t-distribution)
이전에 배웠던 카이제곱 분포는 표본들의 통계량을 통해서, 모집단의 분산을 추정하는데 사용되었습니다.
그러면 모집단의 평균은 무엇으로 추정할 수 있을까요?
이번에 배울 T분포를 통해 모집단의 평균을 추정할 수 있습니다.
T분포는 스튜던트 T 분포, 학생 T 분포 등으로 불리며,
표본분산을 이용하여 정규분포를 따르는 모집단의 평균을 추정할 때 주로 사용되는 분포입니다.
모평균에 대한 신뢰구간이나 가설검정에서 사용됩니다.
T 분포의 정의
두개의 독립인 확률변수 Y , Z를 다음과 같이 정의할 때,
$$Y\; \sim \; \chi^{2}(m)$$
$$Z \; \sim \; N(0, 1^{2})$$
확률변수 X를 다음과 같이 정의하면
$$X = \frac{Z}{(\frac{Y}{m})^{\frac{1}{2}}}$$
이때 X는 자유도 m을 가진 t-distribution을 따른다고 하며, 다음과 같이 나타냅니다.
$$X \; \sim \; T(m)$$
T 분포의 p.d.f
x의 범위는 $-\infty$ 부터 $\infty$ 입니다.
$$f(x\;|\;m) = \frac{\Gamma(\frac{m+1}{2})}{(m\pi)^{\frac{1}{2}} \Gamma(\frac{m}{2})}(1+\frac{x^{2}}{m})^{\frac{-(m+1)}{2}} $$
T 분포의 형태
정규분포와 마찬가지로 대칭(Symmetric)인데, 이때 x=0에 대하여 대칭입니다.
자유도가 커질수록 표준정규분포에 가까워집니다.

T 분포의 속성
평균
확률변수 X가 자유도 m인 t 분포를 따를 때 평균은 다음과 같습니다.
$$E(X) = \infty \;\;\;\;\;\;\; m \leq 1$$
$$E(X) = 0 \;\;\;\;\;\;\; m > 1$$
분산
확률변수 X가 자유도 m인 t 분포를 따를 때 분산은 다음과 같습니다.
$$Var(X) = \frac{m}{m-2} \;\;\;\;\;\;\; m > 2$$
m.g.f
m.g.f가 존재하기 위해서는 다음을 만족해야 합니다.
$$E(|X|^{k}) < \infty$$
이때 k는 항상 1 이상이지만, m이 1보다 작은 경우 평균이 무한대로 발산하므로, 위 식을 만족하지 않으며, 따라서 m.g.f는 존재하지 않습니다.
정규분포의 표본과의 관계
정규분포 N($\mu$ ,$\sigma^2$)를 따르는 모집단으로부터 추출한 n개의 표본 $X_1$, ..., $X_n$에 대하여,
$\sigma$' 을 다음과 같이 정의합니다.
$$\sigma' = \begin{bmatrix} \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}}{n-1} \end{bmatrix}^{\frac{1}{2}}$$
이때 다음이 성립합니다.
$$\frac{\overline{X}_n - \mu}{\frac{\sigma'}{\sqrt{n}}} \;\sim\;T(n-1)$$
증명
다음과 같이 정의하겠습니다.
$$S^{2}_n = \sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}$$
$$Z = \frac{\overline{X}_n - \mu}{\frac{\sigma}{\sqrt{n}}} \;\; \sim \; N(0, \;1)$$
$$Y = \frac{S^{2}_n}{\sigma^{2}}\;\;\sim\; \chi^{2}(n-1)$$
이때 이전에 배웠듯이 Z와 Y는 독립입니다.
또한 Y가 자유도 n-1인 카이제곱 분포를 따르는 이유는 다음과 같습니다.
$$Y = \frac{S^{2}_n}{\sigma^{2}} = \frac{ \sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}}{\sigma^{2}} \; \sim \; \chi^{2}(n-1)$$
이제 U를 다음과 같이 정의하면, t 분포의 정의에 따라, U는 자유도 n-1을 가지는 t 분포를 따릅니다.
$$U = \frac{Z}{(\frac{Y}{n-1})^{\frac{1}{2}}}\;\sim \;T(n-1)$$
또한 U를 다음과 같이 쓸 수 있습니다.
$$U = \frac{\frac{\overline{X}_n-\mu}{\frac{\sigma}{\sqrt{n}}}}{(\frac{S_n^{2}}{\sigma^{2}(n-1)})^{\frac{1}{2}}}$$
이때 분모와 분자의 $\sigma$는 약분되어 다음과 같아집니다.
$$U = \frac{ \sqrt{n}(\overline{X}_n-\mu) }{(\frac{S_n^{2}}{(n-1)})^{\frac{1}{2}}}$$
이때 분모는 $\sigma$' 과 같습니다. 즉 다음의 식이 도출됩니다.
$$U = \frac{ \sqrt{n}(\overline{X}_n-\mu) }{\sigma '} \;\;\;\;\; \because \sigma' = \begin{bmatrix} \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}}{n-1} \end{bmatrix}^{\frac{1}{2}}$$
즉 다음이 증명됩니다.
$$\frac{\overline{X}_n - \mu}{\frac{\sigma'}{\sqrt{n}}} \;\sim\;T(n-1)$$
위의 증명에서 중요한 부분이 있으며, 다음과 같습니다.
1. U의 값 혹은 U의 분포가 모분산 $\sigma$에 의존하지 않습니다.
2. 다음과 같은 정규화된 확률변수 Z에서 $\sigma$(모분산)를 $\sigma$'로 교체하면 U와 같아지며,
따라서 Z의 분포는 SND에서 자유도가 n-1인 t 분포로 바뀝니다.
$$Z = \frac{(\overline{X}_n-\mu)}{\frac{\sigma}{\sqrt{n}}} \; \sim \; N(0, 1^{2})$$
$$\frac{\overline{X}_n - \mu}{\frac{\sigma'}{\sqrt{n}}} \;\sim\;T(n-1)$$
(t 분포는 매우 큰 n에 대하여 SND와 비슷합니다.)
이때 위에서 알아본 것과 같이 U는 σ를 포함하지 않으며, 또한 따라서 σ에 의존적이지 않은 분포를 따릅니다.
따라서 t 분포는 모분산을 모를 때, 모평균을 추정하기 위해 사용이 가능합니다.
모평균을 추정하는 방법은 이후 신뢰구간을 다룰 때 언급하도록 하겠습니다.
$\sigma$'과 $\sigma$에 대한 M.L.E인 $\sigma$^은 각각 다음과 같으며,
$$\sigma '^{2} = \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2} }{n-1}$$
$$\hat{\sigma }^{2} = \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2} }{n}$$
둘 사이에는 다음 관계가 성립합니다.
$$σ'^{2} = (\frac{n}{n-1})\hat{\sigma^{2}}$$
T 분포와 SND
위에서 살펴보았으나 중요하기에 정리하고 넘어가겠습니다.
정규분포를 따르는 확률변수를 정규화할 때,
$\sigma$(모분산) 대신 $\sigma$'을 사용하여 정규화한다면 U와 같아지며,
따라서 정규화된 분포는 SND에서 자유도가 n-1인 t 분포로 바뀝니다.
$$Z = \frac{(\overline{X}_n-\mu)}{\frac{\sigma}{\sqrt{n}}} \; \sim \; N(0, 1^{2})$$
$$\frac{\overline{X}_n - \mu}{\frac{\sigma'}{\sqrt{n}}} \;\sim\;T(n-1)$$
또한 T분포표를 보면 알 수 있듯이 만약 n이 커진다면, σ'는 σ에 가까워집니다.
따라서 Z에서 σ를 σ'로 교체하는 것은 Z의 분포에 큰 영향을 미치지 않습니다.
이러한 이유로 자유도가 n-1인 t 분포는 n이 커질수록 SND에 근접합니다.
$\sigma$'이 먼가용?
이후 불편추정량 부분에서 다시 언급하겠으나, 이해를 돕기 위해 언급하겠습니다.
위에서 정의된 $\sigma$'은 표본분산이며, 실제 분산에 대한 불편추정량입니다.
이전에 평균과 분산을 둘 다 모를 때, 모분산 $\sigma$에 대한 M.L.E 는 $\sigma$^으로 표기하며, 이는 일반적인 분산의 정의에 따른 '편차제곱의 합의 평균'과 동일하며, 다음과 같았습니다.
$$\hat{\sigma}^{2} = \frac{\sum^{n}_{i=1}(X_i - \overline{X}_n)^{2}}{n} $$
그러나 위에서 정의된 표본분산을 불편추정량으로 만들기 위해서 표본분산을 구할 때 n 대신 n-1로 나눕니다.
추정량의 기댓값이 모수와 같아질 때, 해당 추정량을 불편추정량이라 부릅니다.
Reference
https://m.blog.naver.com/mykepzzang/220853827288
[확률과 통계] 50. t 분포, Student's t-Distribution
이번에 다룰 주제는 '스튜던트 t 분포(Student's t-Distribution)'입니다. 간단하게 't-분포'라고 많이 ...
blog.naver.com
8.5 스튜던트 t분포, 카이제곱분포, F분포 — 데이터 사이언스 스쿨
.ipynb .pdf to have style consistency -->
datascienceschool.net
https://1992jhlee.tistory.com/19
불편추정량(Unbiased Estimate) - 표본분산은 왜 n-1로 나누나?
통계를 공부하다 보니 굉장히 불편한 것을 하나 만나게 됐다. 그것은 바로 표본에서 분산을 정의할 때 원래 알던 분산의 정의(편차의 제곱의 평균)가 아닌 다른 방식으로 정의한다는 것이다.
1992jhlee.tistory.com
https://hsm-edu.tistory.com/13
[손으로 푸는 통계 ver1.0] 2. 자유도와 불편추정량 (왜 n-1로 나누나요?)
[통계 기초] 2. 자유도와 불편추정량 (왜 n-1로 나누나요?) 지난시간에 배운 분산 수식은 아래와 같습니다. $\begin{align}V(X)&=E\left [ \left ( X-\mu \right )^2 \right ]\\&=\frac{\..
hsm-edu.tistory.com
https://ko.wikipedia.org/wiki/%EB%B6%88%ED%8E%B8_%EC%B6%94%EC%A0%95%EB%9F%89
불편 추정량 - 위키백과, 우리 모두의 백과사전
추정량의 기대값이 모수와 같아진다면, 이 추정량을 불편추정량이라 한다. 표본평균의 기대값은 모평균과 같으므로 불편추정량이다. 표본분산의 기대값은 모분산과 다르므로 불편추정량이 아
ko.wikipedia.org
https://kongdols-room.tistory.com/152
신뢰구간추정(스튜던트 t-분포, 표준정규분포)-확률과통계(21)
신뢰구간추정(t-분포, 표준정규분포) 본 포스팅에서는 신뢰구간에 대한 설명(Confidence interval)과 스튜던트 t-분포(Student's t-distribution), 표준정규분포(Standard Normal Distribution)을 사용하여 신뢰..
kongdols-room.tistory.com
https://soooprmx.com/%EB%AA%A8%ED%8F%89%EA%B7%A0%EC%9D%98-%EC%B6%94%EC%A0%95/
모평균의 추정 · Wireframe
중심극한 정리에 따르면 모집단의 데이터의 분포에 무관하게, 표본의 크기가 충분히 크다면 표본 평균의 분포는 그 평균의 모평균과 같고, 분산이 모분산을 표본수로 나눈 값인 정규분포에 가
soooprmx.com
'🖥 Computer Science > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] - (23) 불편추정량 (Unbiased estimator) (feat. 표본분산을 n-1로 나누는 이유) (0) | 2022.06.01 |
|---|---|
| [확률과 통계] - (22) 신뢰구간(Confidence Intervals) (0) | 2022.05.31 |
| [확률과 통계] - (20) 표본 평균과 표본 분산의 결합분포 (2) | 2022.05.24 |
| [확률과 통계] - (19) 카이제곱 분포 (Chi-Square Distribution) (3) | 2022.05.23 |
| [확률과 통계] - (18) 통계량(statistic)과 표본분포(Sampling Distribution) (0) | 2022.05.23 |
