BST의 문제점
일반적인 BST(이진 검색 트리)는 데이터가 삽입되는 순서에 따라 한쪽으로 편향되는 형태로 트리가 형성될 수 있습니다.
예를 들어 입력열이 50 -> 30 -> 100 -> 20 -> 150 인 경우 다음과 같습니다.

그러나 입력열이 20 -> 30 -> 50 -> 100 -> 150 인 경우 다음과 같습니다.
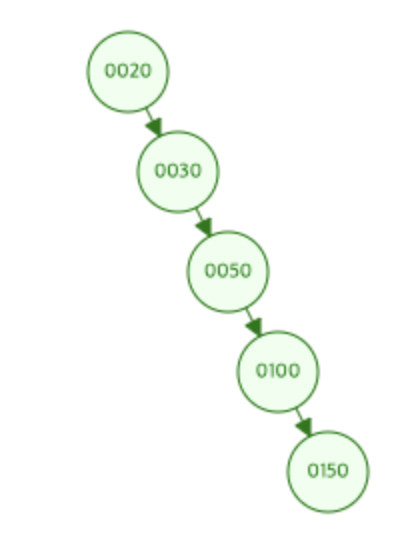
이렇게 BST는 트리의 높이를 $log(n)$ 으로 보장받지 못할 가능성이 있습니다.
트리에서의 성능은 트리의 높이와 연관되어 있습니다.
즉 트리의 높이가 $log(n)$을 보장받지 못한다면, BST의 삽입과 삭제, 검색의 연산 역시 시간복잡도 $O(log(n))$을 보장받지 못합니다.
AVL 트리
AVL 트리는 이진 검색 트리(BST)의 한가지 종류로써 스스로 높이의 균형을 잡는 트리입니다.
AVL 트리를 사용하면 최악의 경우에도 트리의 높이는 $O(log(n))$을 보장받을 수 있게 되어,
삭제, 삽입, 검색등의 작업에서 시작복잡도 $O(log(n))$을 보장받을 수 있는 트리입니다.
AVL 트리는 Balance Factor를 통해 균형을 유지합니다.
AVL 트리의 모든 노드들의 Balance Factor의 값은 -1, 0, 1중에 하나입니다.
Balance Factor
임의의 노드 x에 대하여
x의 왼쪽 서브트리의 높이($h_L$)에서 오른쪽 서브트리의 높이($h_R$)를 뺀 값을 Balance Factor로 정의합니다.
$$BF(x) = h_L(x) - h_R(x)$$
BF가 $|BF| \geq 2$ 인 경우, 트리는 불균형하다고 판단합니다.
불균형 트리
Leaf Node의 높이는 1이라 하겠습니다.
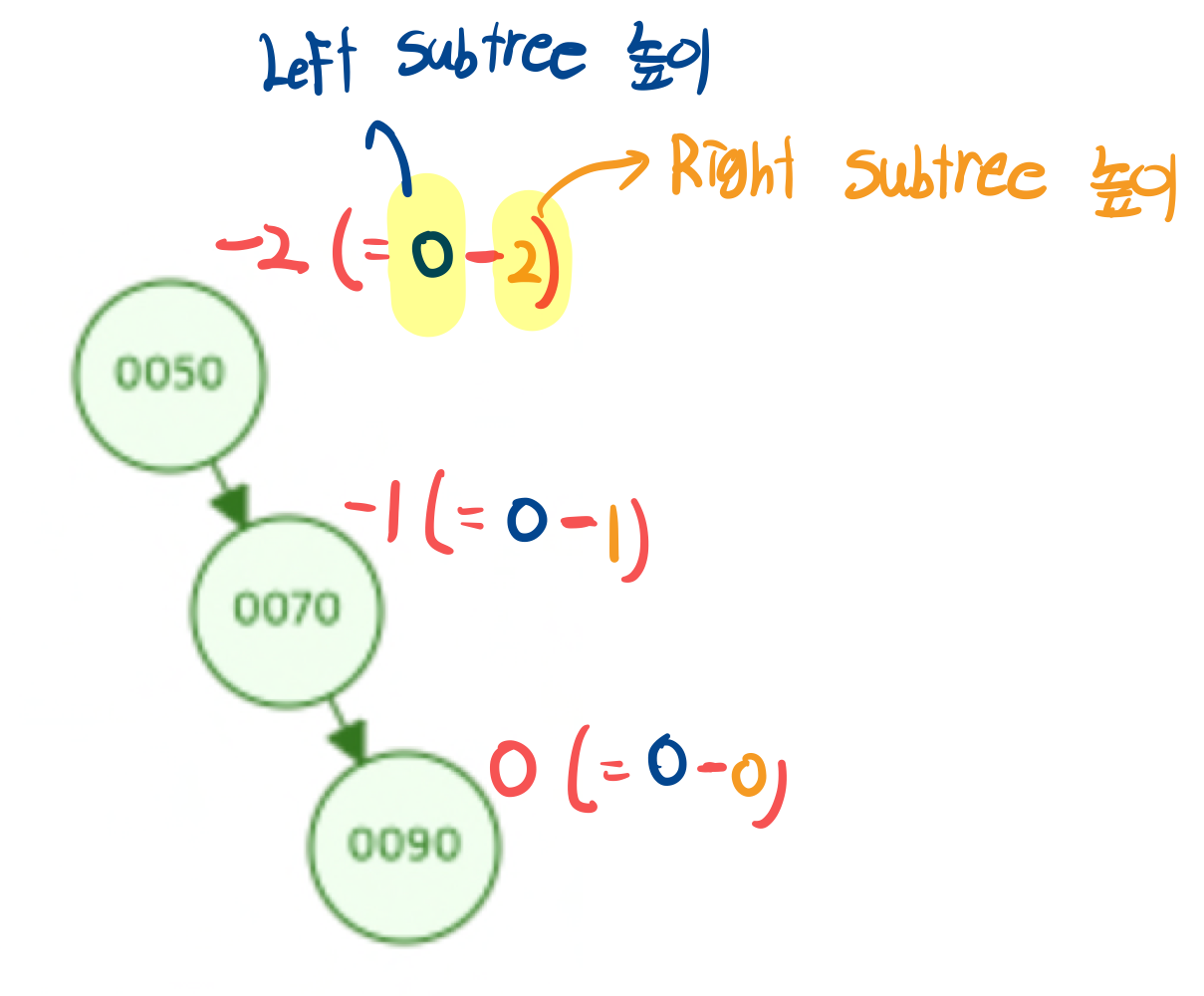
위와 같은 상황에서 AVL 트리는 회전을 통해 균형을 맞춥니다.
균형을 맞추는 방법을 살펴보기 전에 AVL트리의 높이가 $O(log(n))$이 보장되는 원리를 살펴보겠습니다.
AVL 트리의 높이(Height)
우선 높이가 h인 AVL트리가 가질 수 있는 최소한의 노드 수를 생각해 보도록 하겠습니다.
최소한의 노드 수를 $N_h$ 라 하면 다음과 같습니다.
$$N_h=\left\{\begin{matrix} 0 & h=0\\ 1& h=1\\ N_{h-1} + N_{h-2} + 1& h \geq 2\\ \end{matrix}\right.$$
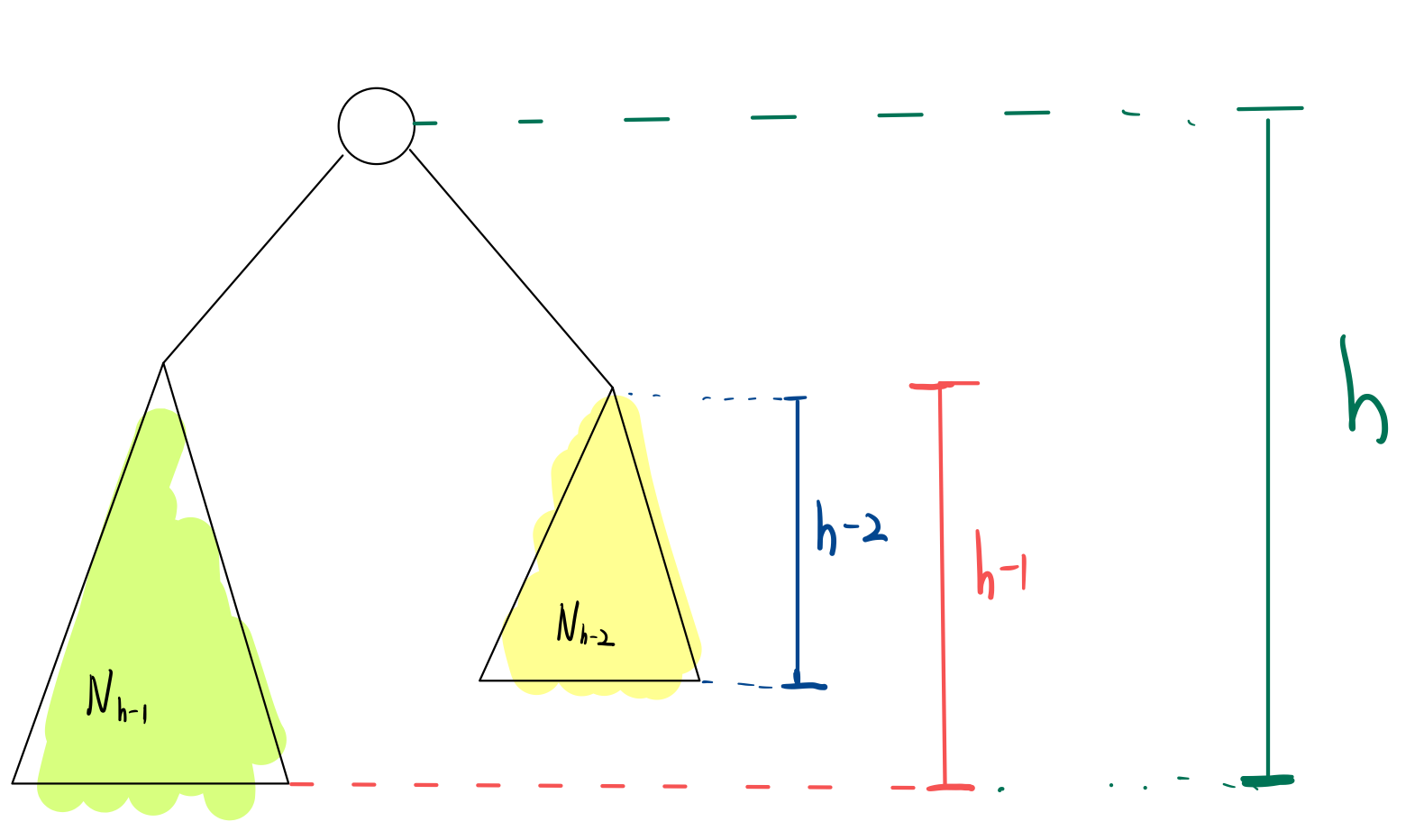
이제 Fibonacci Tree를 살펴보겠습니다.
주어진 높이를 가진 AVL트리 중 최소의 노드 개수를 갖는 트리를 Fibonacci Tree라 합니다.
Fibonacci Tree의 노드 수와 Fibonacci 수의 관계
높이가 h인 Fibonacci Tree의 노드 수는 다음과 같습니다.
$$N_h=\left\{\begin{matrix} 0 & h=0\\ 1& h=1\\ N_{h-1} + N_{h-2} + 1& h \geq 2\\ \end{matrix}\right.$$
n번째 Fibonacci 수는 다음과 같습니다.
$$F_h=\left\{\begin{matrix} 0 & n=0\\ 1& n=1\\ F_{h-1} + F_{h-2} & h \geq 2\\ \end{matrix}\right.$$
이 둘 사이에는 다음 관계식이 성립합니다.
$$N_h = F_{h+2} - 1 $$
Fibonacci Tree의 높이
피보나치 수 $F_h$는 다음에 근사함이 알려져 있습니다.
$$F_h \approx \phi^{h} / \sqrt{5} \;\;\;\;\;\;\;\; \phi = (1 + \sqrt{5})/2$$
Fibonacci Tree의 노드 수와 Fibonacci 수의 관계식을 통해 다음이 성립합니다.
$$N_h = F_{h+2} - 1 \approx (\phi^{h+2} / \sqrt{5})-1$$
N_h를 n이라 하겠습니다.
$$(\phi^{h+2} / \sqrt{5})-1 = n$$
$$\phi^{h+2} = \sqrt{5} (n+1)$$
$$ h + 2 = log_{\phi}(\sqrt{5} (n+1))$$
$$ h = log_{\phi}(\sqrt{5} (n+1)) - 2 = O(lon (n))$$
Fibonacci 트리는 주어진 높이에 대해 최소한의 노드 수를 가진다고 하였습니다.
이는 즉 주어진 노드수가 가질 수 있는 최대 높이를 가지는 것을 의미합니다.
n을 높이가 h인 AVL 트리가 가진 노드 수라고 하겠습니다.
높이 h인 Full Binary Tree가 가질 수 있는 노드의 총 개수는 다음과 같습니다.
$$2^{h} - 1$$
그리고 높이가 h인 AVL 트리가 가질 수 있는 최소 노드의 개수, 즉 높이 h인 Fibonacci Tree의 노드의 수는 다음과 같습니다.
$$N_h \approx (\phi^{h+2} / \sqrt{5})-1 $$
n는 다음 범위에 속합니다.
$$N_h \leq n \leq 2^{h} - 1$$
$$if(n == (2^{h} - 1)), \;\; 2^h = n + 1 \; \to \; h =O(log(n))$$
$$if(n == N_h ) \; \to \; h =O(log(n))$$
따라서 h는 $O(log(n))$이 보장됩니다.
불균형 문제
다음과 같은 4가지 종류가 있습니다.
- LL 문제
- RR 문제
- LR 문제
- RL 문제
LL문제
삽입 또는 삭제로 인해 Left-Left로 서브 트리가 비대해지는 것을 LL문제라 합니다.
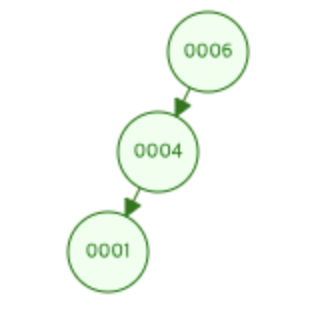
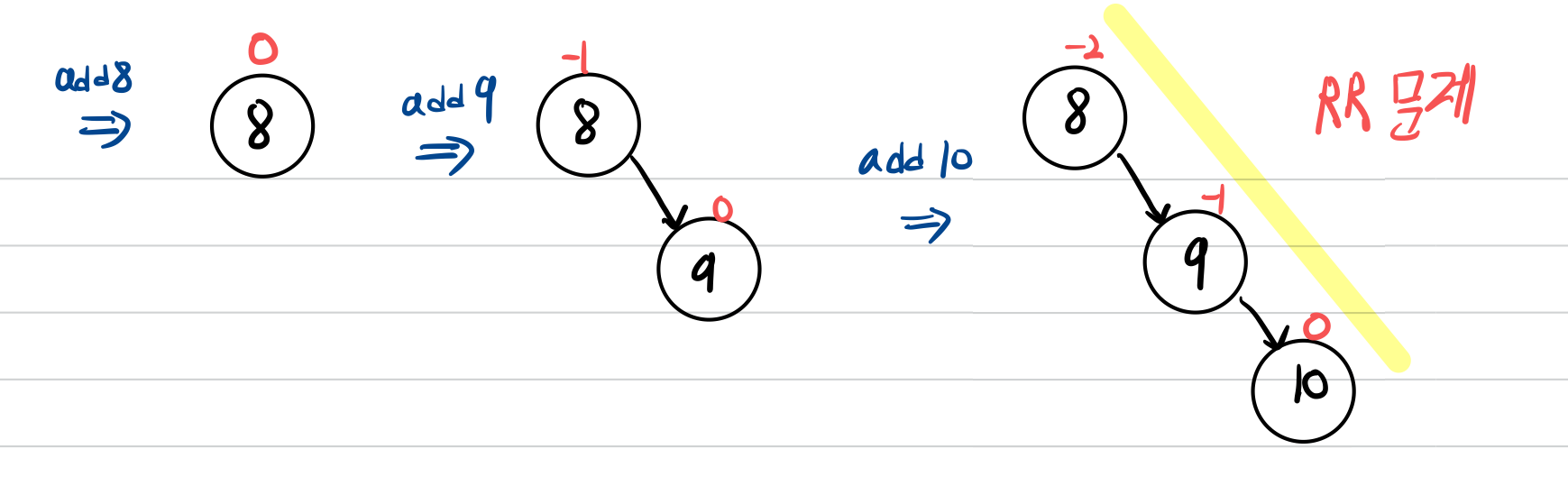
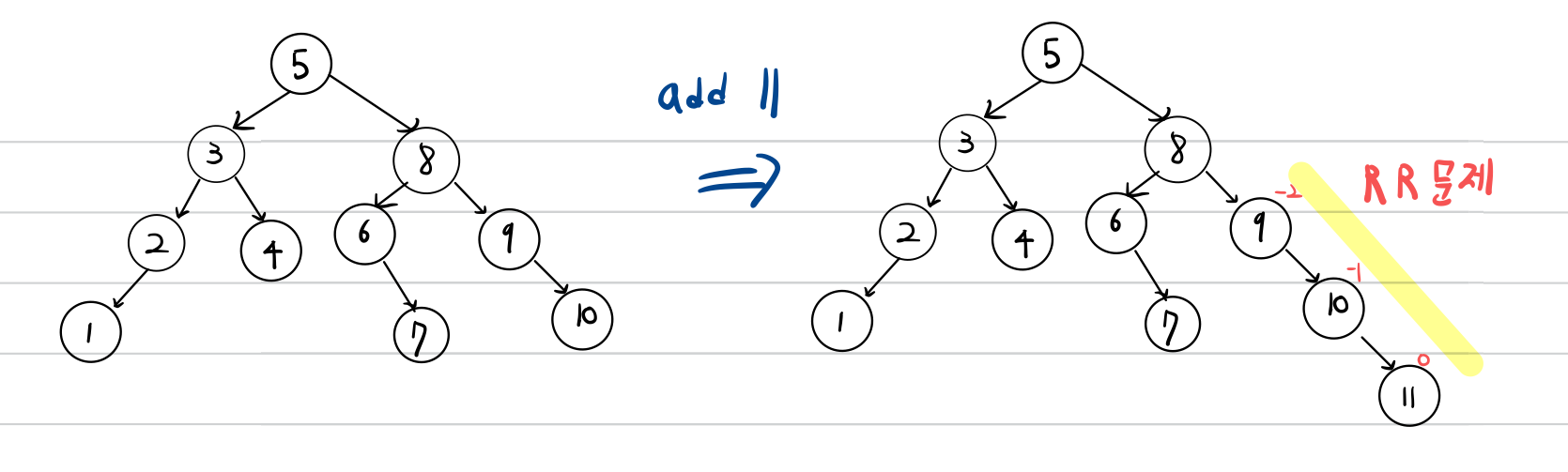
RR문제
삽입 또는 삭제로 인해 Right-Right로 서브 트리가 비대해지는 것을 RR문제라 합니다.
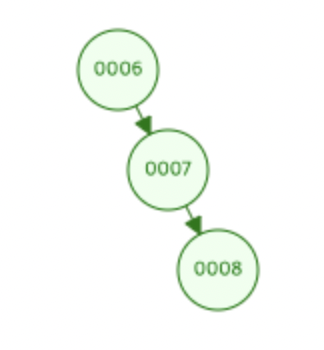
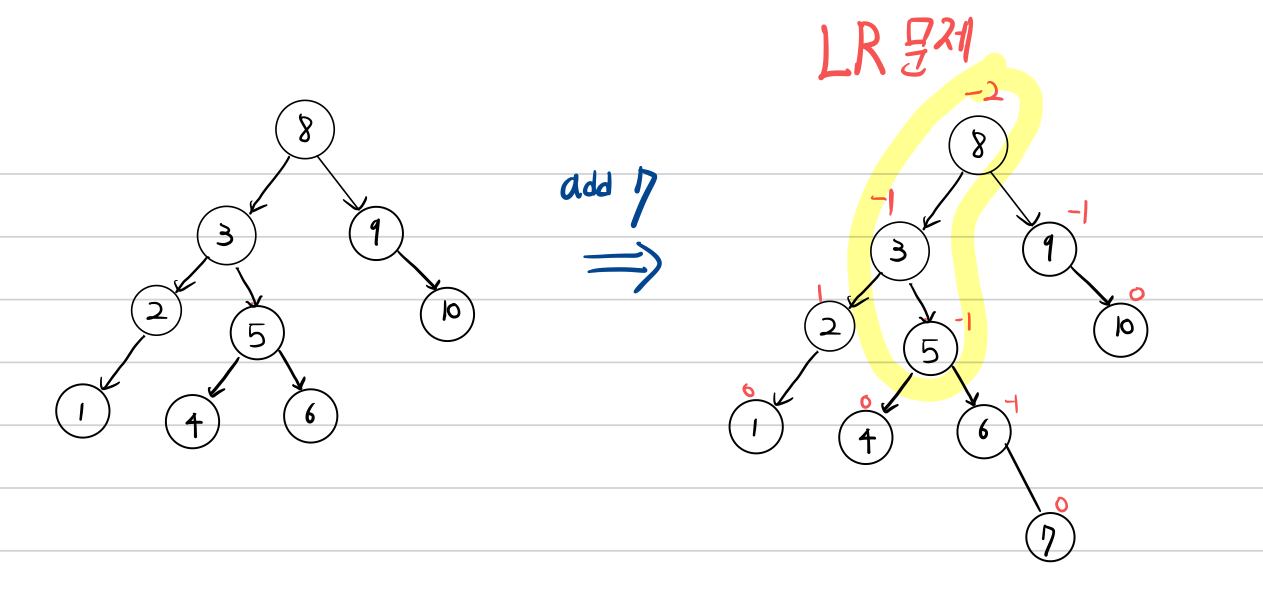
LR문제
삽입 또는 삭제로 인해 Left-Right로 서브 트리가 비대해지는 것을 LR문제라 합니다.
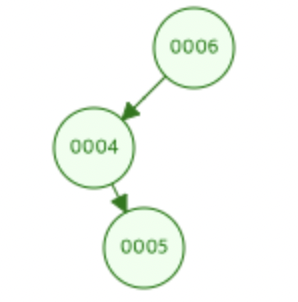
RL문제
삽입 또는 삭제로 인해 Right-Left로 서브 트리가 비대해지는 것을 RL문제라 합니다.

AVL 트리의 회전
다음과 같은 4가지 종류가 있습니다.
- LL 회전
- RR 회전
- LR 회전
- RL 회전
회전하는 동안 회전의 중심이 되는 노드의 left, right 서브트리 관계를 유지해주어야 합니다.
즉 left에 존재한 것은 회전 이후에도 left,
즉 right에 존재한 것은 회전 이후에도 right에 존재해야 합니다.
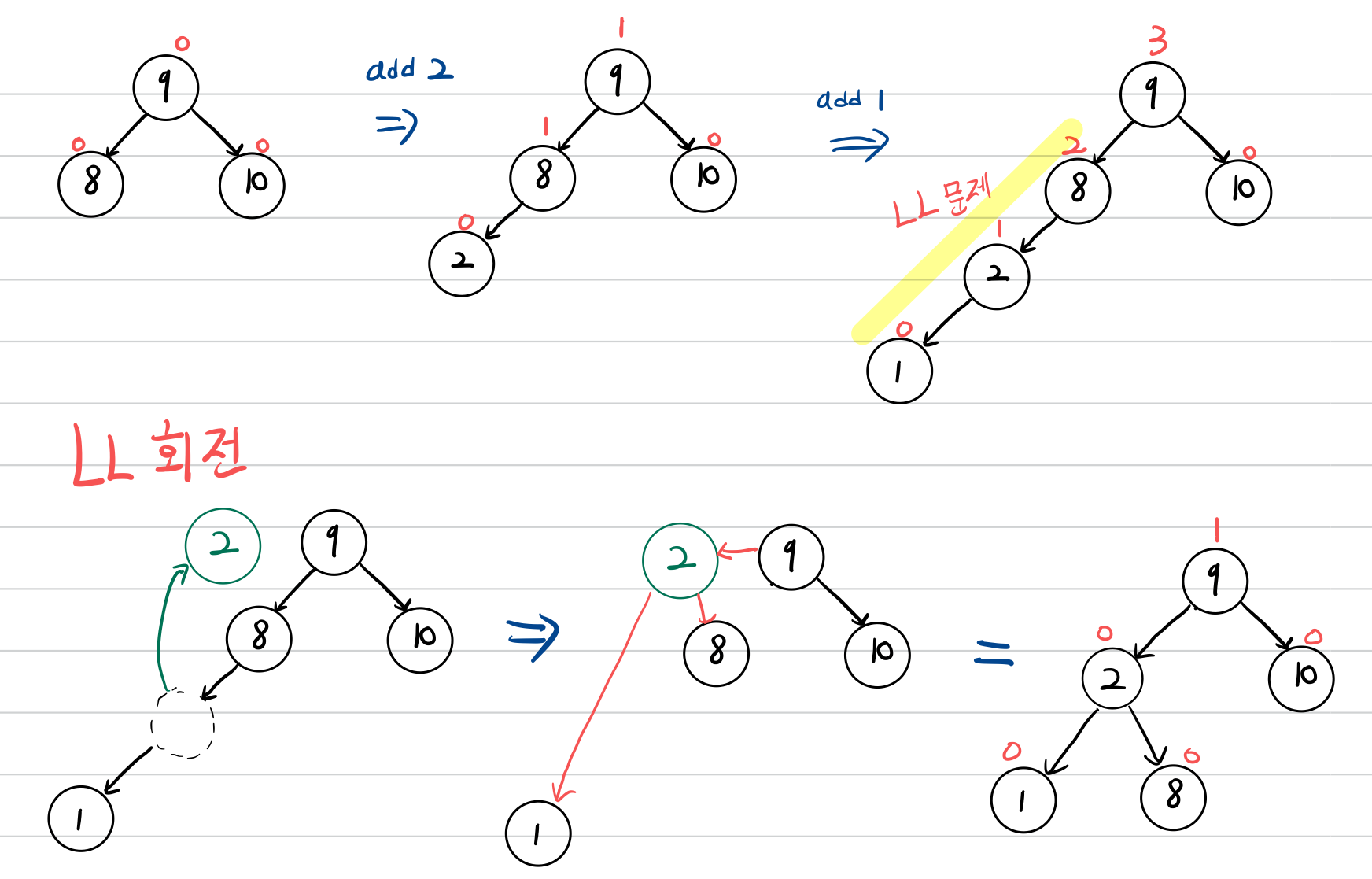
LL 회전
LL문제를 해결하기 위한 회전입니다.
LL 회전은 노드의 Balance Factor가 2일때, 그 좌측 서브트리의 루트노드의 BF가 1인 경우 균형을 맞추기 위한 회전입니다.
LL 회전은 오른쪽으로 돌리는 작업입니다.

BF가 2인 노드의 왼쪽 서브트리를 루트 노드로 만들면서,
왼쪽 서브트리의 오른쪽 서브트리를 기존 루트의 왼쪽 서브트리에 삽입합니다.
좀 더 간단하게 생각하면, 가운데 노드를 가장 위로 올려주는 작업을 하면 됩니다.
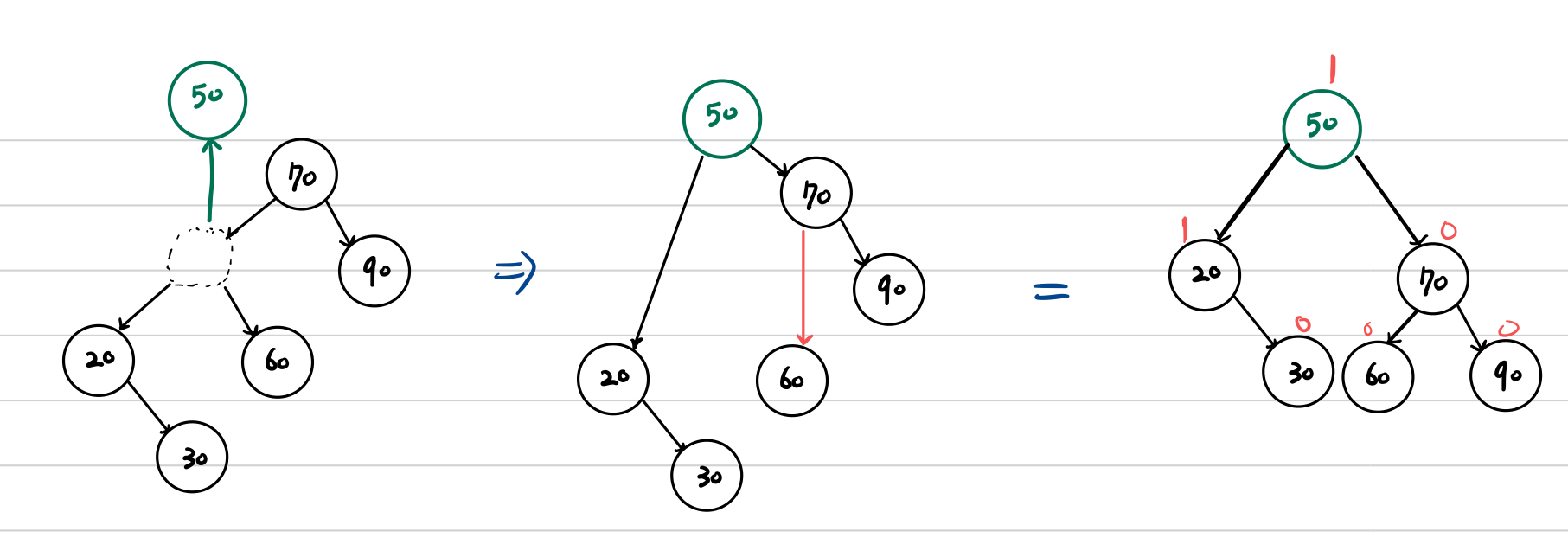
RR 회전
RR문제를 해결하기 위한 회전입니다.
RR 회전은 노드의 Balance Factor가 -2일때, 그 우측 서브트리의 루트노드가 -1인 경우 균형을 맞추기 위한 회전입니다.
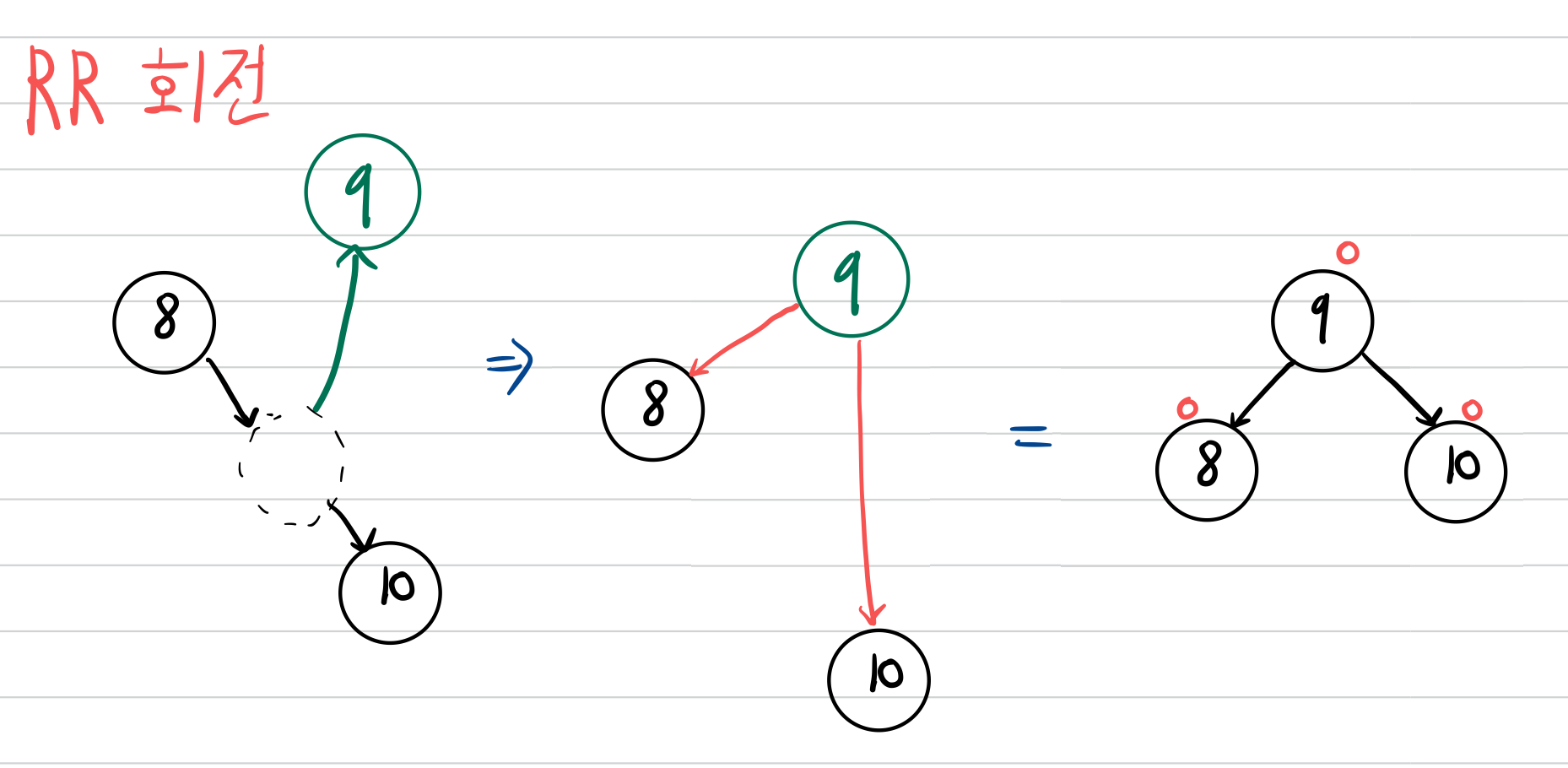
RR 회전은 왼쪽으로 돌리는 작업입니다.
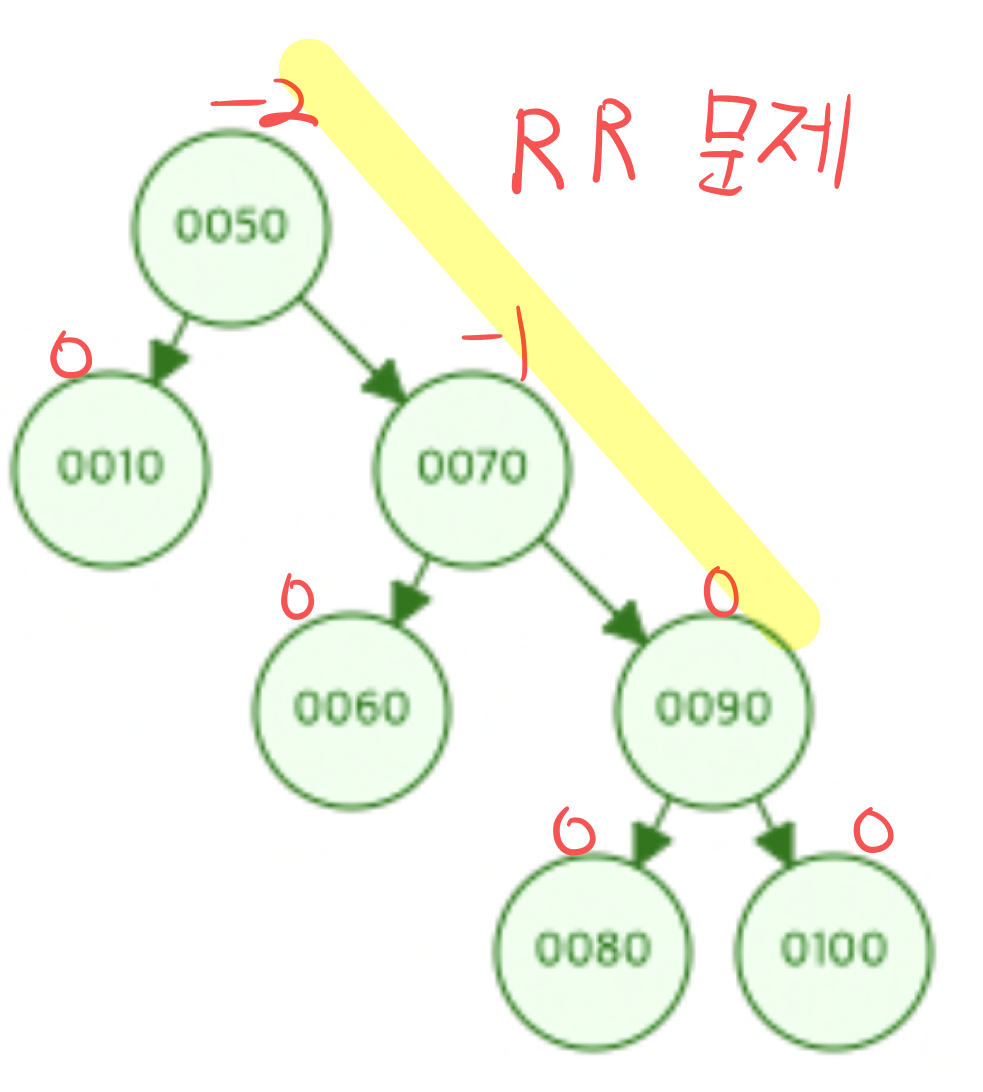
BF가 -2인 노드의 오른쪽 서브트리를 루트 노드로 만들면서,
오른쪽 서브트리의 왼쪽 서브트리를 기존 루트의 오른쪽 서브트리에 삽입합니다.
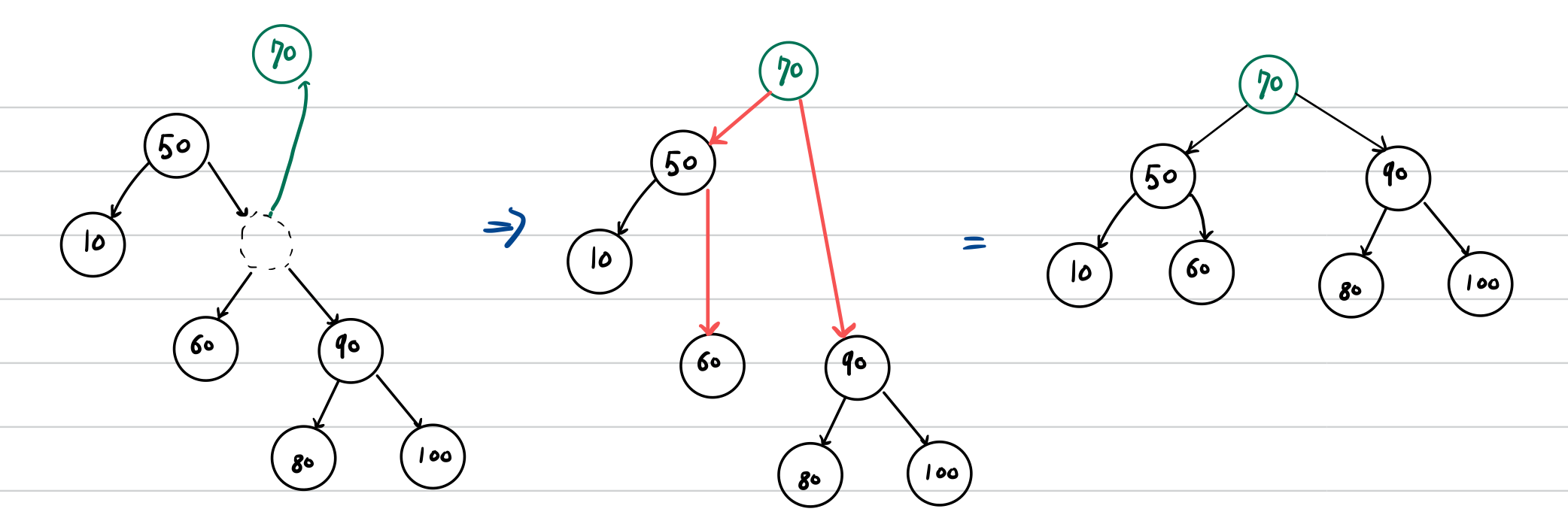
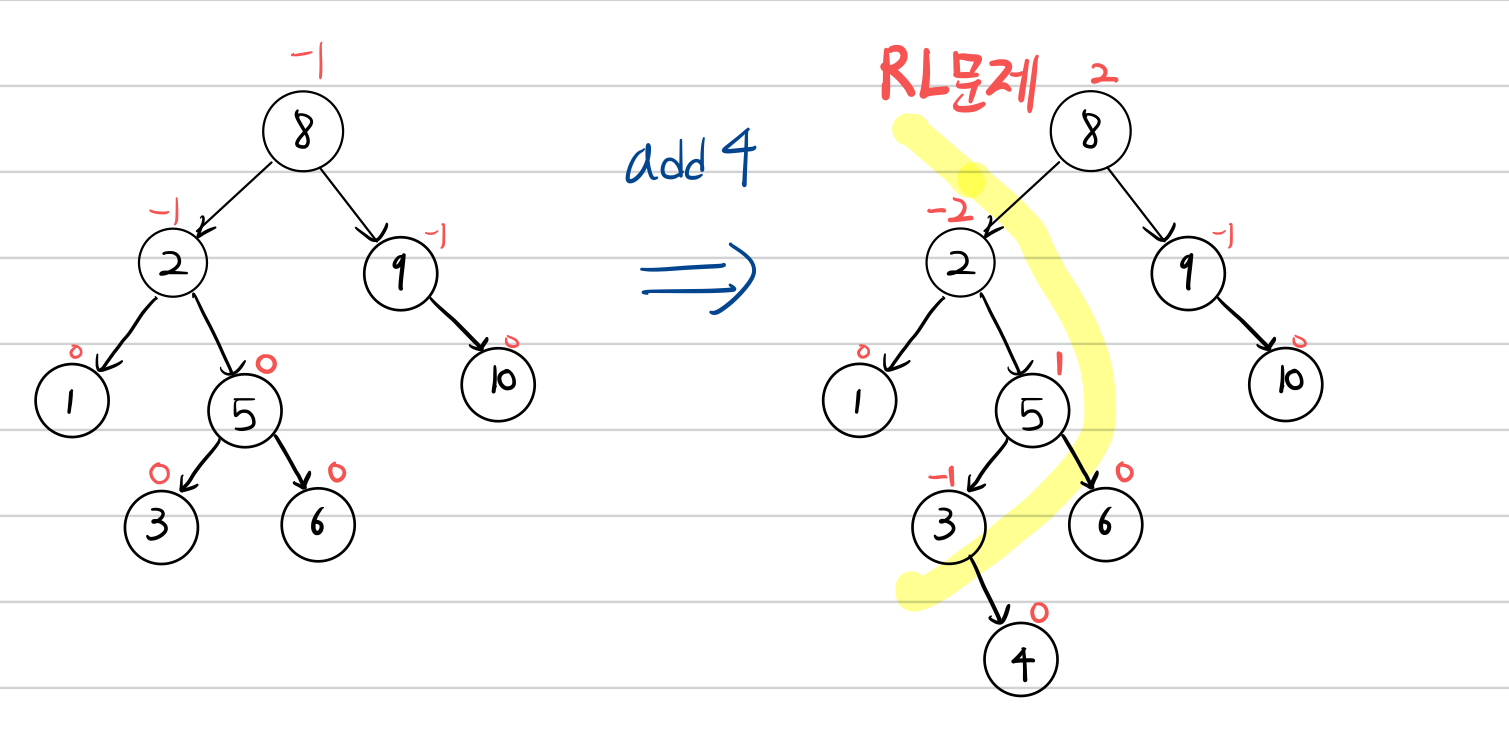
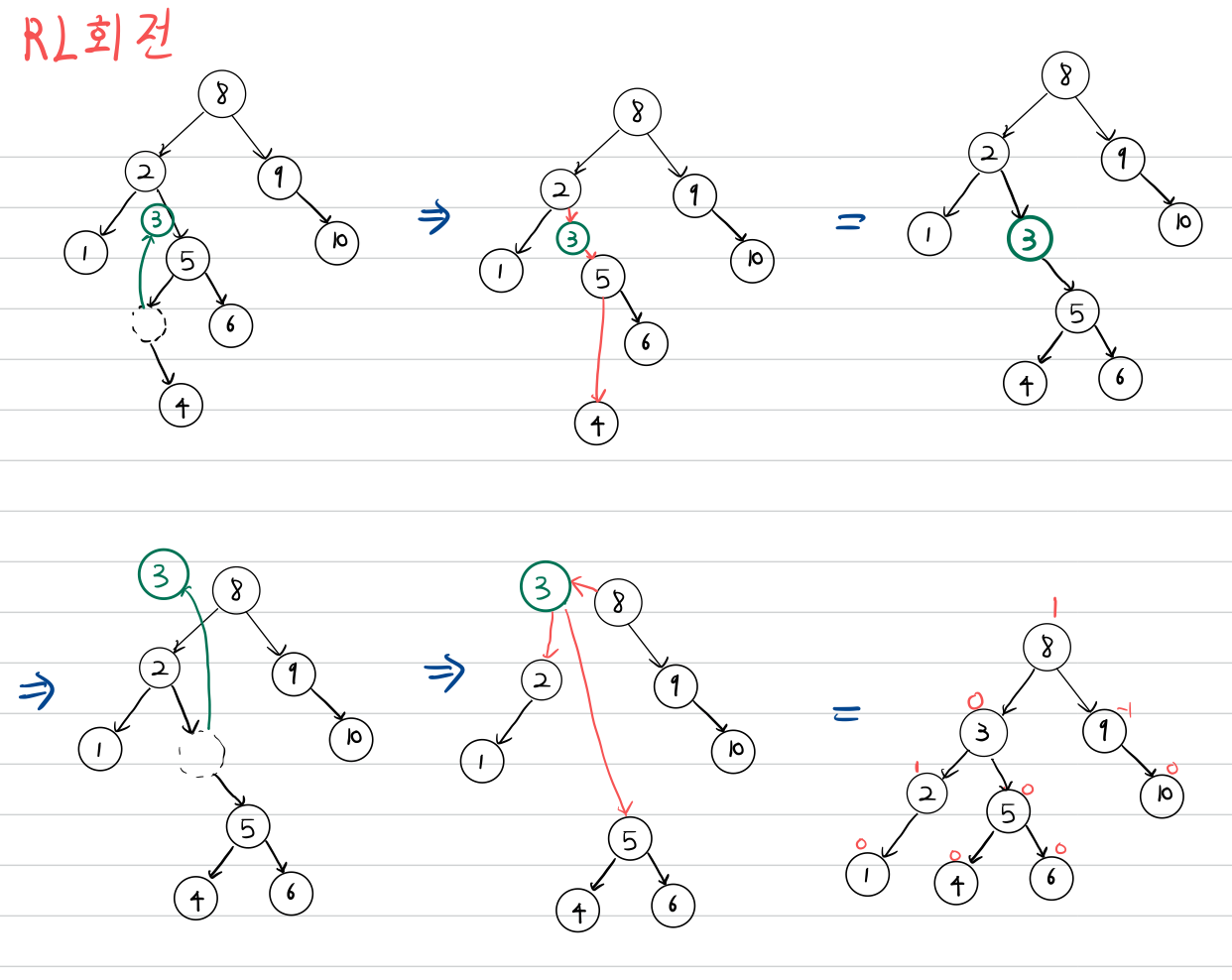
RL 회전
RL문제를 해결하기 위한 회전입니다.
RL 회전은 노드의 Balance Factor가 -2일때, 그 우측 서브트리의 루트노드가 1인 경우 균형을 맞추기 위한 회전입니다.
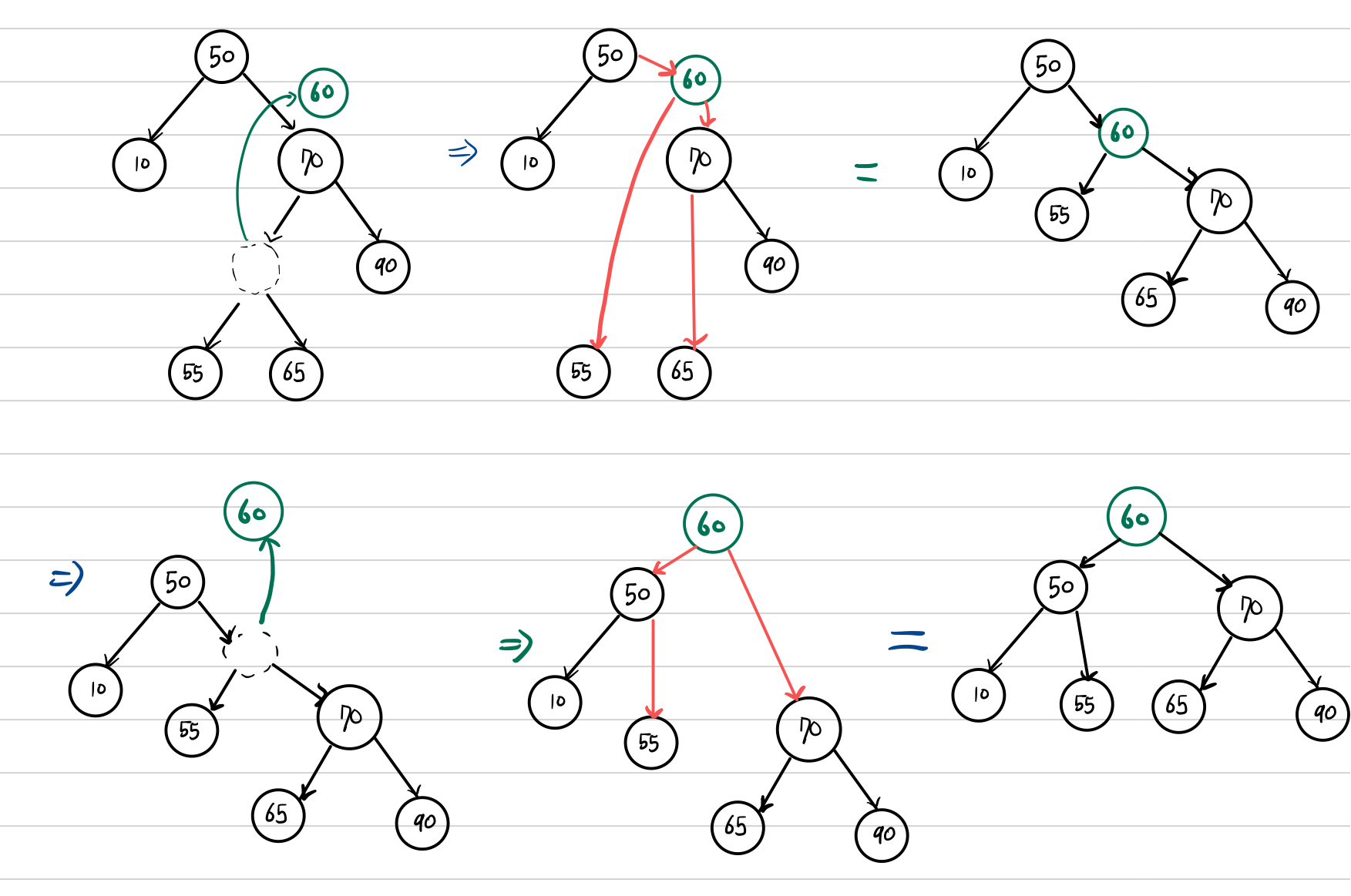
RL 회전은 오른쪽으로 돌리고, 왼쪽으로 돌리는 작업입니다.
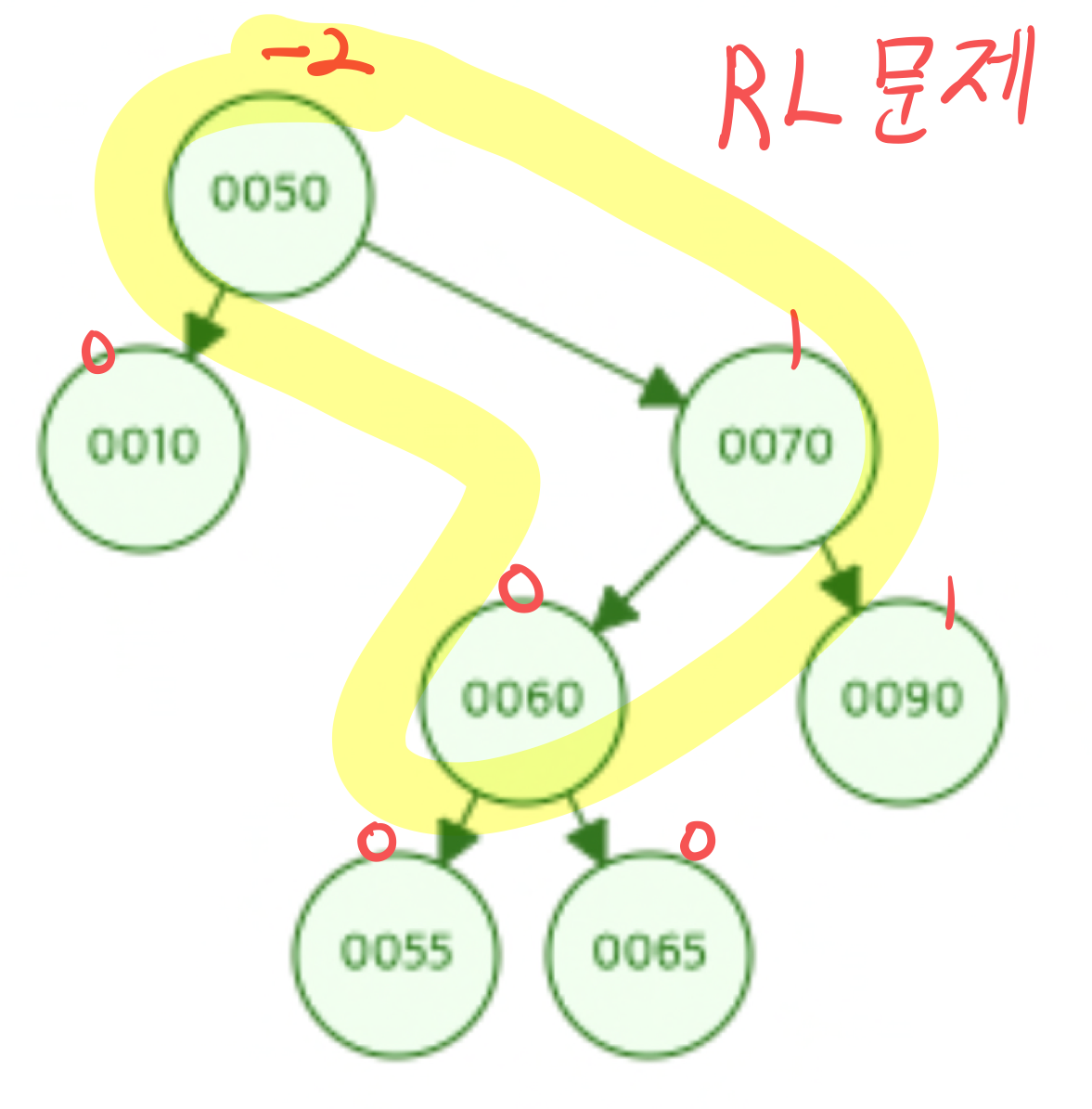
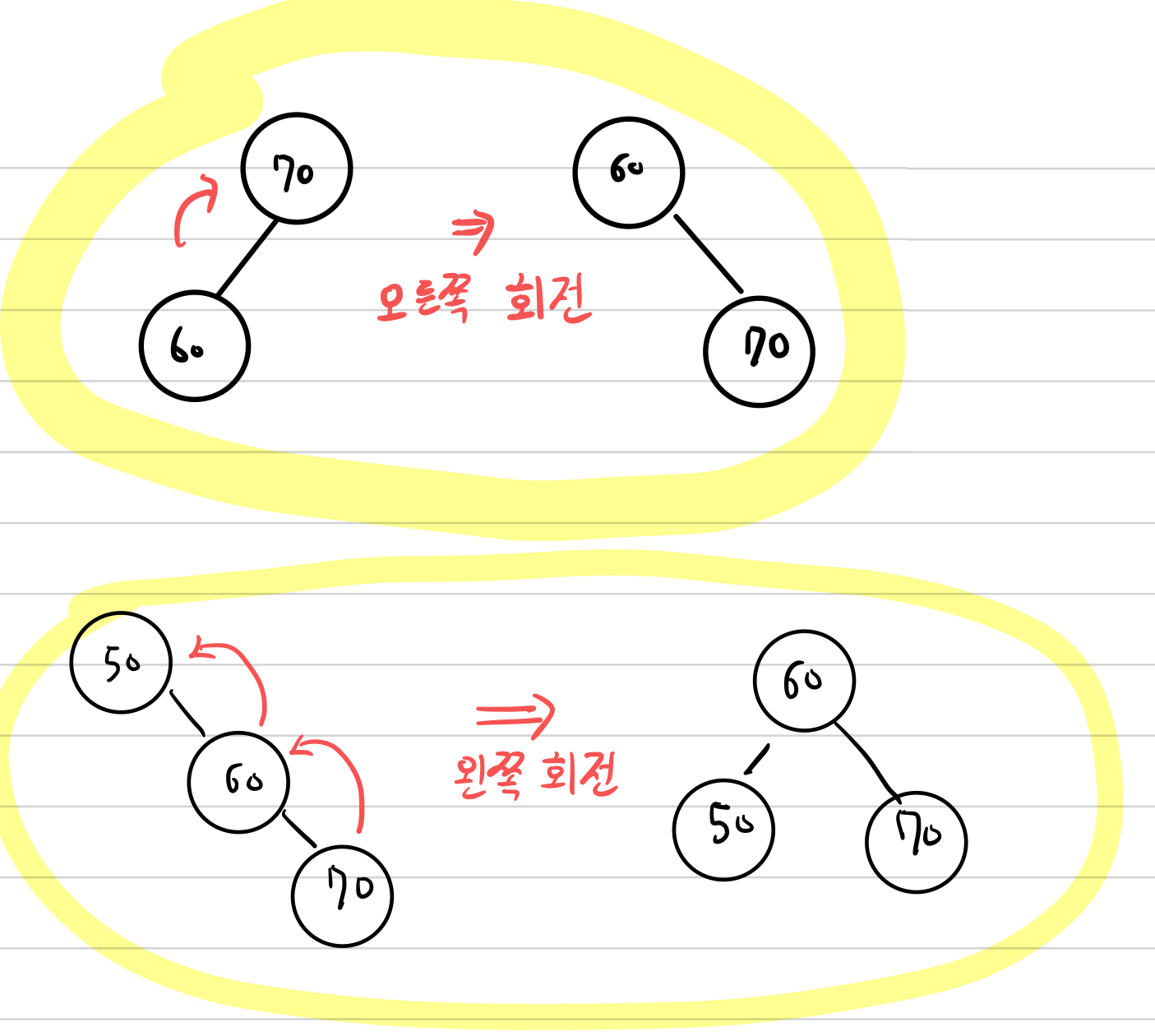
BF가 -2인 노드의 오른쪽 서브트리(BF가 1)의 왼쪽 서브트리에 대하여,
LL회전을 한 후, (오른쪽으로 돌리고)(높이가 1 증가)
RR 회전을 해줍니다. (왼쪽으로 돌리고)(높이가 1 증가)
두번에 걸쳐서 노드를 루트노드로 만들어주는 작업을 거칩니다.
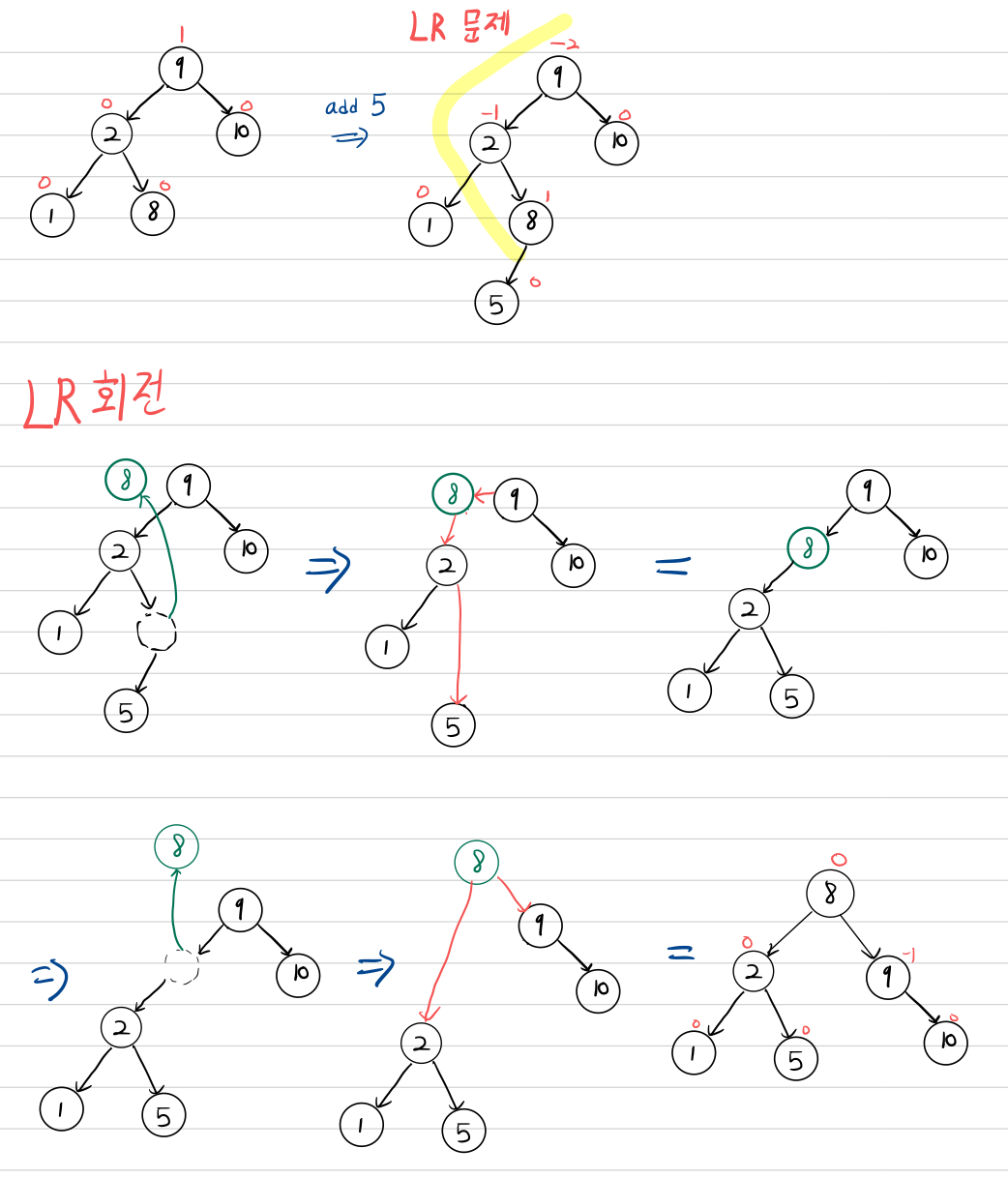
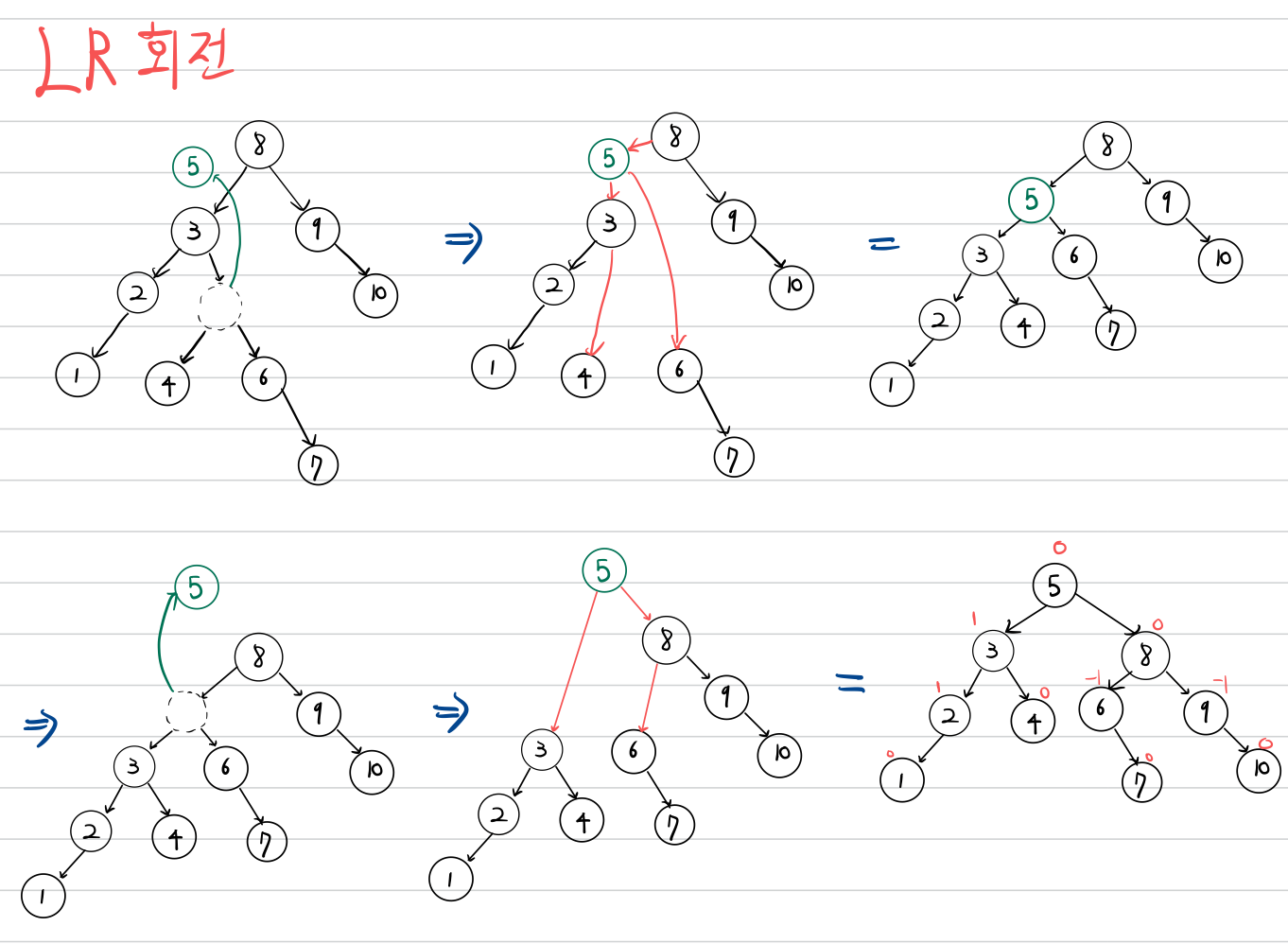
LR 회전
LR 문제를 해결하기 위한 회전입니다.
LR 회전은 노드의 Balance Factor가 2일때, 그 좌측 서브트리의 루트노드가 -1인 경우 균형을 맞추기 위한 회전입니다.
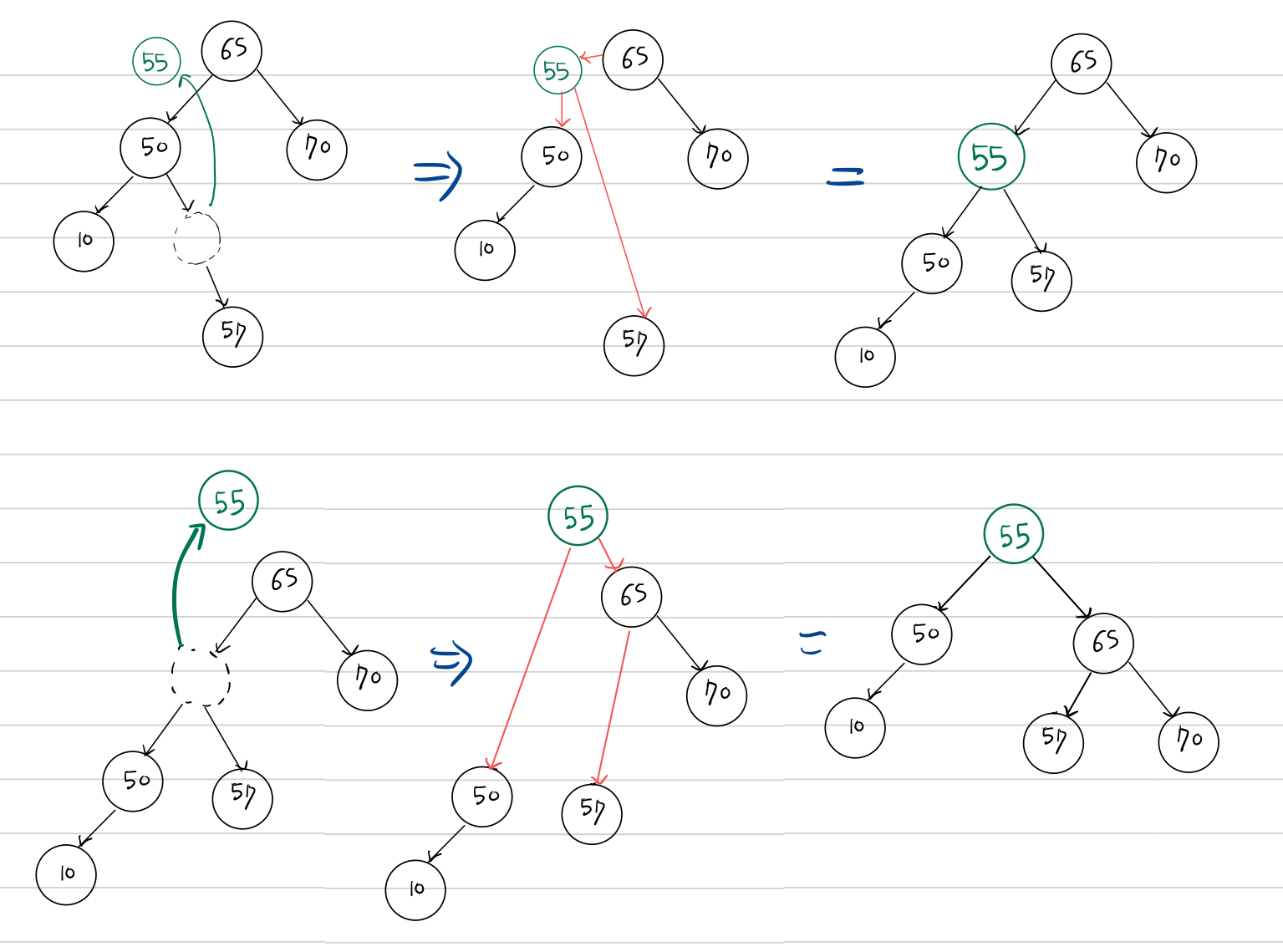
LR 회전은 왼쪽으로 돌리고, 오른쪽으로 돌리는 작업입니다.
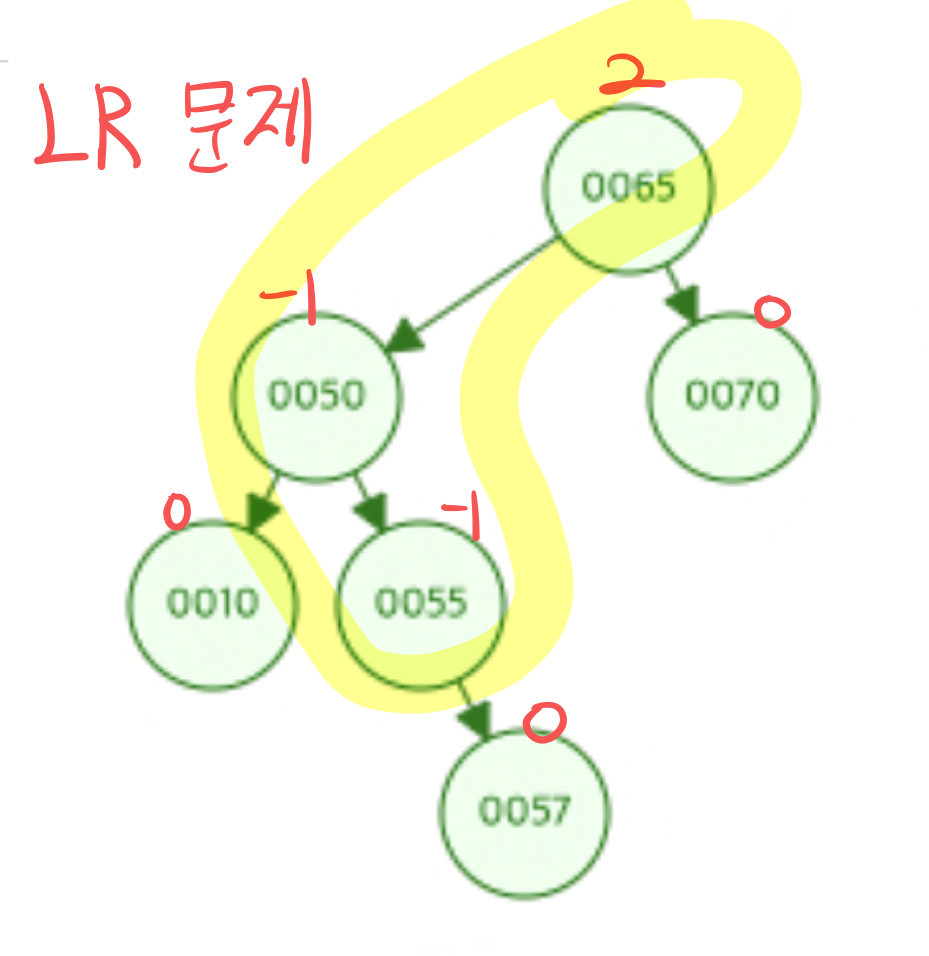
BF가 2인 노드의 왼쪽 서브트리(BF가 -1)의 오른쪽 서브트리에 대하여,
RR회전을 한 후, (왼쪽으로 돌리고)(높이가 1 증가)
LL 회전을 해줍니다. (오른쪽으로 돌리고)(높이가 1 증가)
두번에 걸쳐서 노드를 루트노드로 만들어주는 작업을 거칩니다.
알고리즘
private void rebalance(Node root) {
if (root.right().height() > root.left().height()+1 ) {//Right로 편향된 경우
if (root.right().left().height() > root.right().right().height() ) { // RL회전이 필요한 경우
root.right().rotateRight(); // root의 right에 대하여 LL 회전(오른쪽으로 돌리기)
}
root.rotateLeft();//RR회전 (왼쪽으로 돌리기)
}
else if (root.right().height() + 1 < root.left().height() ) {//Right로 편향된 경우
if (root.left().right().height() > root.left().left().height() ) { // LR회전이 필요한 경우
root.left().rotateLeft(); // root의 left 대하여 RR 회전(왼쪽으로 돌리기)
}
root.rotateRight();//LL회전 (오른쪽으로 돌리기)
}
}
예시
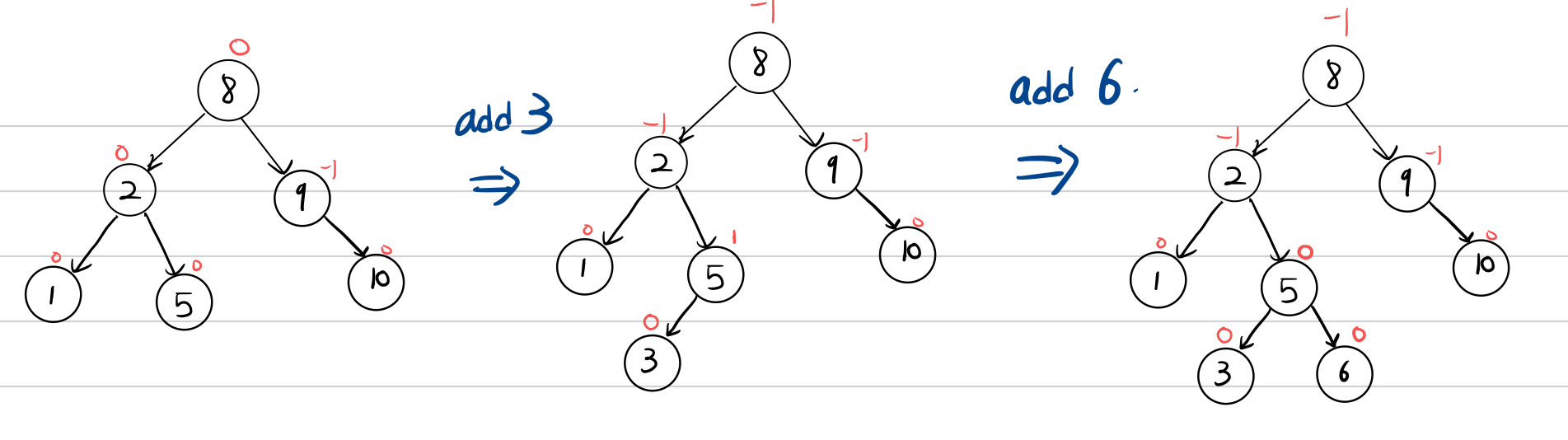
다음 순서로 입력이 들어온다고 하겠습니다.
$$8 \to 9 \to 10 \to 2 \to 1 \to 5 \to 3 \to 6 \to 4 \to 7 \to 11 \to 12$$
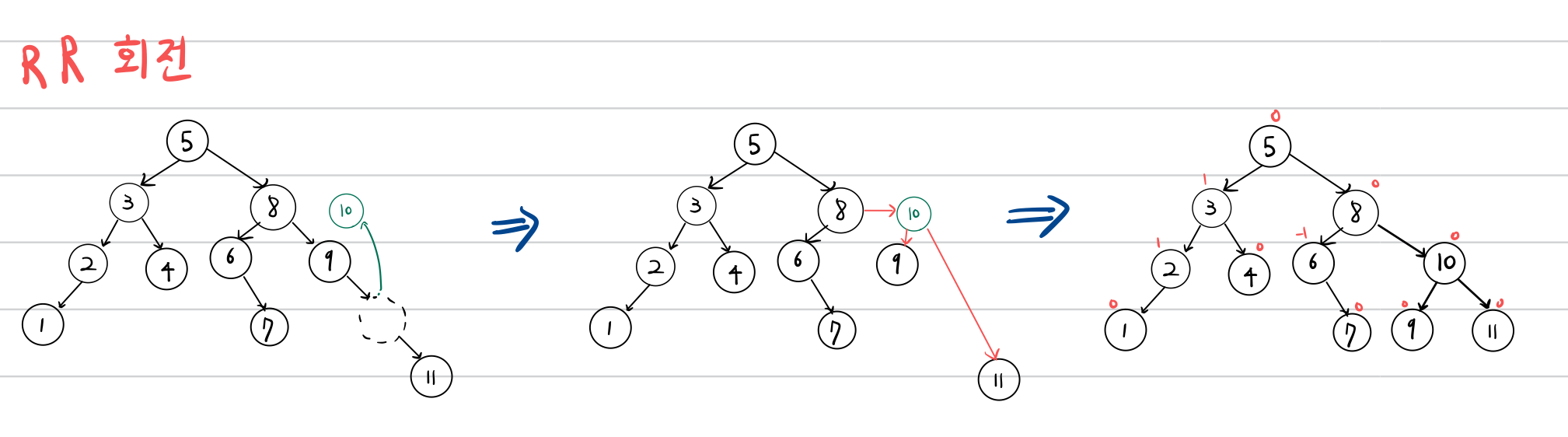
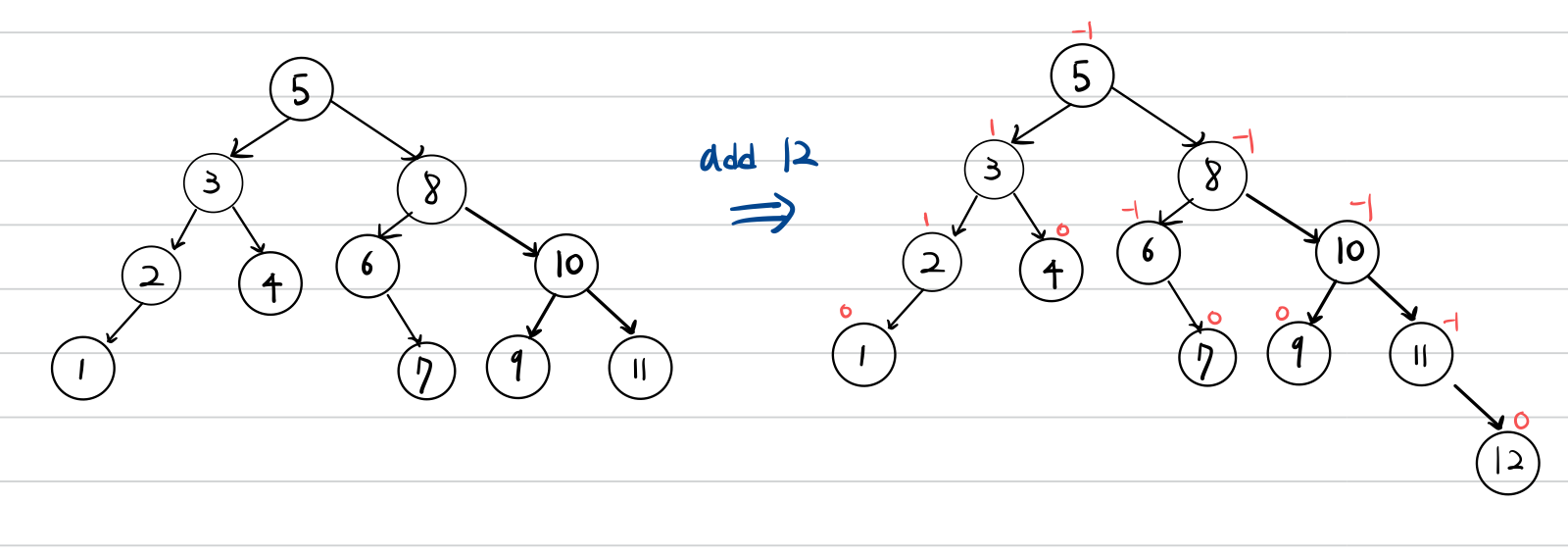
Reference
https://www.youtube.com/watch?v=syGPNOhsnI4&t=454s
'🖥 Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] - B-Tree (0) | 2022.06.10 |
|---|---|
| [자료구조] - 2-3 Tree (4) | 2022.06.10 |
| [자료구조] - Hash(해시) (0) | 2022.06.07 |
| [자료구조] - 딥(Deap : Double Endeded Heap) (0) | 2022.06.07 |
| [자료구조] - 우선순위 큐(Priority Queue) (0) | 2022.06.06 |
BST의 문제점
일반적인 BST(이진 검색 트리)는 데이터가 삽입되는 순서에 따라 한쪽으로 편향되는 형태로 트리가 형성될 수 있습니다.
예를 들어 입력열이 50 -> 30 -> 100 -> 20 -> 150 인 경우 다음과 같습니다.

그러나 입력열이 20 -> 30 -> 50 -> 100 -> 150 인 경우 다음과 같습니다.

이렇게 BST는 트리의 높이를 $log(n)$ 으로 보장받지 못할 가능성이 있습니다.
트리에서의 성능은 트리의 높이와 연관되어 있습니다.
즉 트리의 높이가 $log(n)$을 보장받지 못한다면, BST의 삽입과 삭제, 검색의 연산 역시 시간복잡도 $O(log(n))$을 보장받지 못합니다.
AVL 트리
AVL 트리는 이진 검색 트리(BST)의 한가지 종류로써 스스로 높이의 균형을 잡는 트리입니다.
AVL 트리를 사용하면 최악의 경우에도 트리의 높이는 $O(log(n))$을 보장받을 수 있게 되어,
삭제, 삽입, 검색등의 작업에서 시작복잡도 $O(log(n))$을 보장받을 수 있는 트리입니다.
AVL 트리는 Balance Factor를 통해 균형을 유지합니다.
AVL 트리의 모든 노드들의 Balance Factor의 값은 -1, 0, 1중에 하나입니다.
Balance Factor
임의의 노드 x에 대하여
x의 왼쪽 서브트리의 높이($h_L$)에서 오른쪽 서브트리의 높이($h_R$)를 뺀 값을 Balance Factor로 정의합니다.
$$BF(x) = h_L(x) - h_R(x)$$
BF가 $|BF| \geq 2$ 인 경우, 트리는 불균형하다고 판단합니다.
불균형 트리
Leaf Node의 높이는 1이라 하겠습니다.

위와 같은 상황에서 AVL 트리는 회전을 통해 균형을 맞춥니다.
균형을 맞추는 방법을 살펴보기 전에 AVL트리의 높이가 $O(log(n))$이 보장되는 원리를 살펴보겠습니다.
AVL 트리의 높이(Height)
우선 높이가 h인 AVL트리가 가질 수 있는 최소한의 노드 수를 생각해 보도록 하겠습니다.
최소한의 노드 수를 $N_h$ 라 하면 다음과 같습니다.
$$N_h=\left\{\begin{matrix} 0 & h=0\\ 1& h=1\\ N_{h-1} + N_{h-2} + 1& h \geq 2\\ \end{matrix}\right.$$

이제 Fibonacci Tree를 살펴보겠습니다.
주어진 높이를 가진 AVL트리 중 최소의 노드 개수를 갖는 트리를 Fibonacci Tree라 합니다.
Fibonacci Tree의 노드 수와 Fibonacci 수의 관계
높이가 h인 Fibonacci Tree의 노드 수는 다음과 같습니다.
$$N_h=\left\{\begin{matrix} 0 & h=0\\ 1& h=1\\ N_{h-1} + N_{h-2} + 1& h \geq 2\\ \end{matrix}\right.$$
n번째 Fibonacci 수는 다음과 같습니다.
$$F_h=\left\{\begin{matrix} 0 & n=0\\ 1& n=1\\ F_{h-1} + F_{h-2} & h \geq 2\\ \end{matrix}\right.$$
이 둘 사이에는 다음 관계식이 성립합니다.
$$N_h = F_{h+2} - 1 $$
Fibonacci Tree의 높이
피보나치 수 $F_h$는 다음에 근사함이 알려져 있습니다.
$$F_h \approx \phi^{h} / \sqrt{5} \;\;\;\;\;\;\;\; \phi = (1 + \sqrt{5})/2$$
Fibonacci Tree의 노드 수와 Fibonacci 수의 관계식을 통해 다음이 성립합니다.
$$N_h = F_{h+2} - 1 \approx (\phi^{h+2} / \sqrt{5})-1$$
N_h를 n이라 하겠습니다.
$$(\phi^{h+2} / \sqrt{5})-1 = n$$
$$\phi^{h+2} = \sqrt{5} (n+1)$$
$$ h + 2 = log_{\phi}(\sqrt{5} (n+1))$$
$$ h = log_{\phi}(\sqrt{5} (n+1)) - 2 = O(lon (n))$$
Fibonacci 트리는 주어진 높이에 대해 최소한의 노드 수를 가진다고 하였습니다.
이는 즉 주어진 노드수가 가질 수 있는 최대 높이를 가지는 것을 의미합니다.
n을 높이가 h인 AVL 트리가 가진 노드 수라고 하겠습니다.
높이 h인 Full Binary Tree가 가질 수 있는 노드의 총 개수는 다음과 같습니다.
$$2^{h} - 1$$
그리고 높이가 h인 AVL 트리가 가질 수 있는 최소 노드의 개수, 즉 높이 h인 Fibonacci Tree의 노드의 수는 다음과 같습니다.
$$N_h \approx (\phi^{h+2} / \sqrt{5})-1 $$
n는 다음 범위에 속합니다.
$$N_h \leq n \leq 2^{h} - 1$$
$$if(n == (2^{h} - 1)), \;\; 2^h = n + 1 \; \to \; h =O(log(n))$$
$$if(n == N_h ) \; \to \; h =O(log(n))$$
따라서 h는 $O(log(n))$이 보장됩니다.
불균형 문제
다음과 같은 4가지 종류가 있습니다.
- LL 문제
- RR 문제
- LR 문제
- RL 문제
LL문제
삽입 또는 삭제로 인해 Left-Left로 서브 트리가 비대해지는 것을 LL문제라 합니다.

RR문제
삽입 또는 삭제로 인해 Right-Right로 서브 트리가 비대해지는 것을 RR문제라 합니다.

LR문제
삽입 또는 삭제로 인해 Left-Right로 서브 트리가 비대해지는 것을 LR문제라 합니다.

RL문제
삽입 또는 삭제로 인해 Right-Left로 서브 트리가 비대해지는 것을 RL문제라 합니다.

AVL 트리의 회전
다음과 같은 4가지 종류가 있습니다.
- LL 회전
- RR 회전
- LR 회전
- RL 회전
회전하는 동안 회전의 중심이 되는 노드의 left, right 서브트리 관계를 유지해주어야 합니다.
즉 left에 존재한 것은 회전 이후에도 left,
즉 right에 존재한 것은 회전 이후에도 right에 존재해야 합니다.
LL 회전
LL문제를 해결하기 위한 회전입니다.
LL 회전은 노드의 Balance Factor가 2일때, 그 좌측 서브트리의 루트노드의 BF가 1인 경우 균형을 맞추기 위한 회전입니다.
LL 회전은 오른쪽으로 돌리는 작업입니다.

BF가 2인 노드의 왼쪽 서브트리를 루트 노드로 만들면서,
왼쪽 서브트리의 오른쪽 서브트리를 기존 루트의 왼쪽 서브트리에 삽입합니다.
좀 더 간단하게 생각하면, 가운데 노드를 가장 위로 올려주는 작업을 하면 됩니다.

RR 회전
RR문제를 해결하기 위한 회전입니다.
RR 회전은 노드의 Balance Factor가 -2일때, 그 우측 서브트리의 루트노드가 -1인 경우 균형을 맞추기 위한 회전입니다.
RR 회전은 왼쪽으로 돌리는 작업입니다.

BF가 -2인 노드의 오른쪽 서브트리를 루트 노드로 만들면서,
오른쪽 서브트리의 왼쪽 서브트리를 기존 루트의 오른쪽 서브트리에 삽입합니다.

RL 회전
RL문제를 해결하기 위한 회전입니다.
RL 회전은 노드의 Balance Factor가 -2일때, 그 우측 서브트리의 루트노드가 1인 경우 균형을 맞추기 위한 회전입니다.
RL 회전은 오른쪽으로 돌리고, 왼쪽으로 돌리는 작업입니다.


BF가 -2인 노드의 오른쪽 서브트리(BF가 1)의 왼쪽 서브트리에 대하여,
LL회전을 한 후, (오른쪽으로 돌리고)(높이가 1 증가)
RR 회전을 해줍니다. (왼쪽으로 돌리고)(높이가 1 증가)
두번에 걸쳐서 노드를 루트노드로 만들어주는 작업을 거칩니다.

LR 회전
LR 문제를 해결하기 위한 회전입니다.
LR 회전은 노드의 Balance Factor가 2일때, 그 좌측 서브트리의 루트노드가 -1인 경우 균형을 맞추기 위한 회전입니다.
LR 회전은 왼쪽으로 돌리고, 오른쪽으로 돌리는 작업입니다.

BF가 2인 노드의 왼쪽 서브트리(BF가 -1)의 오른쪽 서브트리에 대하여,
RR회전을 한 후, (왼쪽으로 돌리고)(높이가 1 증가)
LL 회전을 해줍니다. (오른쪽으로 돌리고)(높이가 1 증가)
두번에 걸쳐서 노드를 루트노드로 만들어주는 작업을 거칩니다.

알고리즘
private void rebalance(Node root) {
if (root.right().height() > root.left().height()+1 ) {//Right로 편향된 경우
if (root.right().left().height() > root.right().right().height() ) { // RL회전이 필요한 경우
root.right().rotateRight(); // root의 right에 대하여 LL 회전(오른쪽으로 돌리기)
}
root.rotateLeft();//RR회전 (왼쪽으로 돌리기)
}
else if (root.right().height() + 1 < root.left().height() ) {//Right로 편향된 경우
if (root.left().right().height() > root.left().left().height() ) { // LR회전이 필요한 경우
root.left().rotateLeft(); // root의 left 대하여 RR 회전(왼쪽으로 돌리기)
}
root.rotateRight();//LL회전 (오른쪽으로 돌리기)
}
}
예시
다음 순서로 입력이 들어온다고 하겠습니다.
$$8 \to 9 \to 10 \to 2 \to 1 \to 5 \to 3 \to 6 \to 4 \to 7 \to 11 \to 12$$












Reference
https://www.youtube.com/watch?v=syGPNOhsnI4&t=454s
'🖥 Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] - B-Tree (0) | 2022.06.10 |
|---|---|
| [자료구조] - 2-3 Tree (4) | 2022.06.10 |
| [자료구조] - Hash(해시) (0) | 2022.06.07 |
| [자료구조] - 딥(Deap : Double Endeded Heap) (0) | 2022.06.07 |
| [자료구조] - 우선순위 큐(Priority Queue) (0) | 2022.06.06 |