Deap이란?
완전 이진 트리(Complete Binary Tree)이며, 비어있거나 다음을 만족시키는 자료구조입니다.
1. Root 노드는 아무런 요소를 가지고 있지 않습니다.
2. 왼쪽 서브트리는 min-heap 입니다.
3. 오른쪽 서브트리는 max-heap 입니다.
만약 오른쪽 서브트리가 비어있지 않은 경우 $i_{left}$ 를 왼쪽 서브트리의 임의의 요소라 하겠습니다.
$j_{right}$ 를 $i_{left}$ 에 대응되는 우측 서브트리의 요소라고 하겠습니다.
만약 $j_{right}$ 가 존재하지 않는 경우,
$j_{right}$ 의 위치는 $i_{left}$ 의 부모(parent)노드에 대응되는max-heap의 원소가 됩니다.
항상 $i_{left}$ 는 $j_{right}$ 보다 작거나 같은 값을 가져야만 합니다.
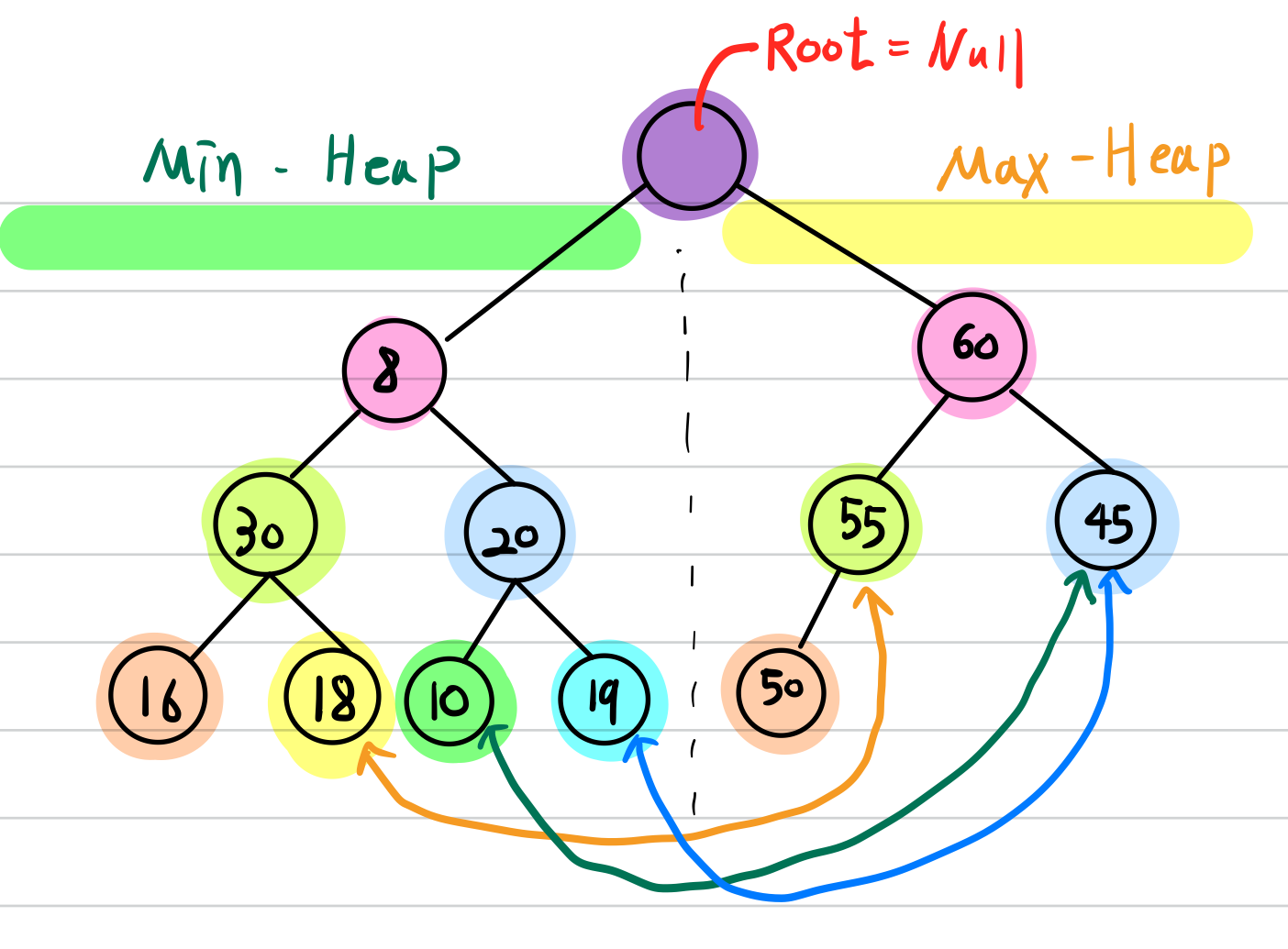
Deap에서 대응하는 요소 찾기
공통적으로 사용되는 성질부터 알아보도록 하겠습니다.
(루트의 인덱스를 항상 1로 생각합니다.)
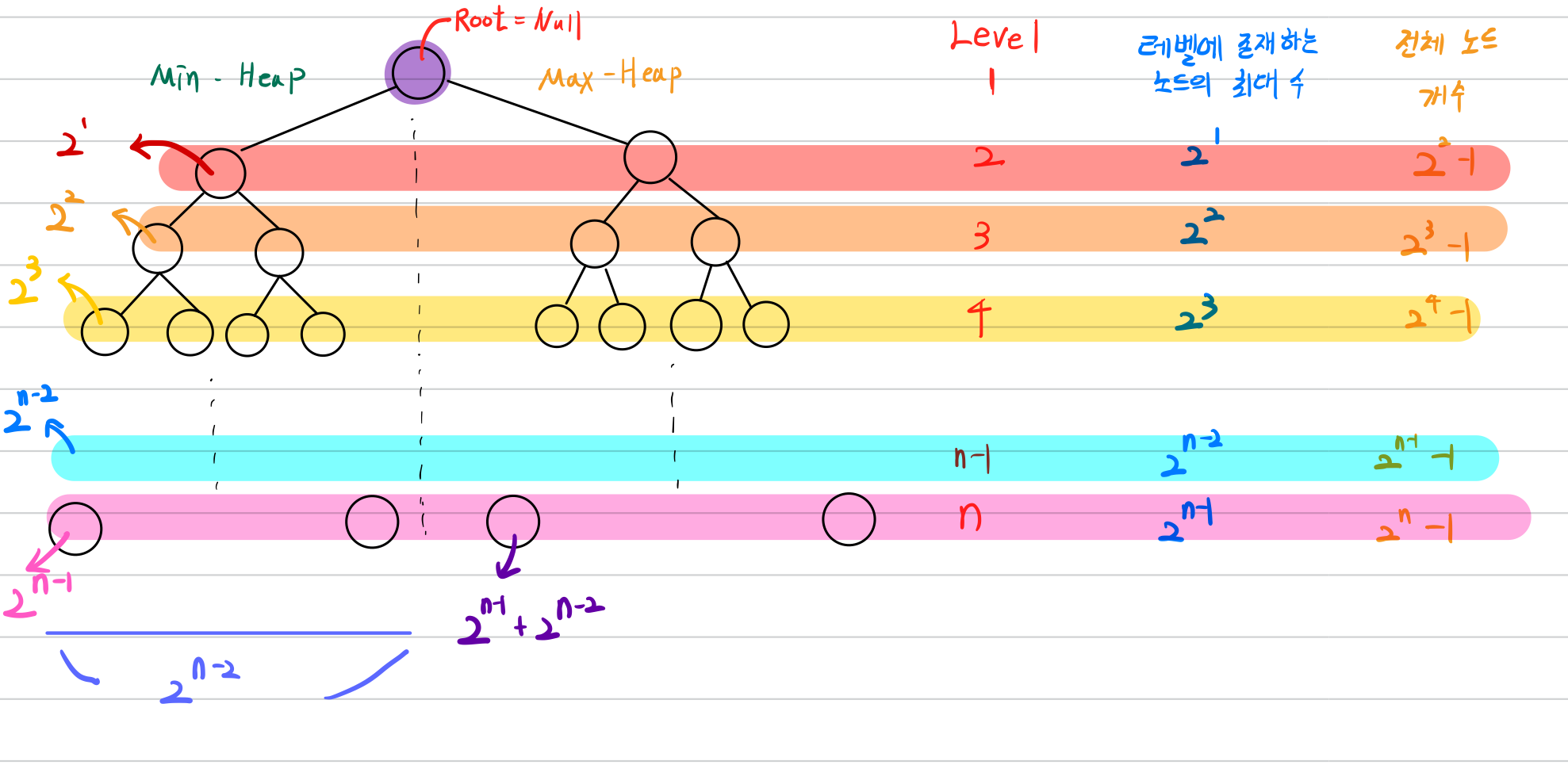
완전 이진 트리에서, 레벨 i에서 존재할 수 있는 노드의 최대 수는 다음과 같습니다.
$$2^{i-1}$$
또한 레벨 i인 트리가 가질 수 있는 노드의 최대 수는 다음과 같습니다.
$$2^{i} - 1$$
위 두 성질을 종합하면, 다음과 같습니다.
레벨 i의 최좌측 노드의 인덱스 = 레벨 i-1 인 트리가 가질 수 있는 최대 노드의 수 + 1
$$= 2^{i-1}$$
레벨 i의 최우측 노드의 인덱스 = 레벨 i-1 인 트리가 가질 수 있는 최대 노드의 수
$$ = 2^{i} - 1$$
인덱스가 주어졌을 때 레벨 구하기
노드의 인덱스가 n인 경우, 해당 레벨 l은 다음과 같습니다.
$$l = [log_2(n)] + 1$$
증명
레벨 l의 시작 인덱스 ~ 레벨 l의 끝 인덱스 사이에 n이 존재해야 하며, n은 정수입니다.
$$2^{l-1} \leq n \leq 2^{l}-1 < 2^{l}$$
$$l-1 \leq log_2(n) < l$$
이때 l-1과 l은 정수이며, 1밖에 차이나지 않기에 [log2(n)]는 l-1이 됩니다.
따라서 l = [log2(n)] + 1이 됩니다.
Min Heap에 대응하는 Max Heap의 요소 찾기
Min Heap에 속한 노드의 인덱스를 i라고 하겠습니다.
대응하는 Max Heap의 요소의 인덱스를 j라고 하면
$$j = 2^{[log_2(i)] - 1} + i$$
이때 j가 존재하지 않는 경우, 즉 j >n(노드의 수)인 경우 j는 다음과 같습니다.
$$j = j/2$$
증명
i번째 노드의 레벨 k는 다음과 같습니다.
$$k = [log_2(i)] + 1$$
레벨 k에 존재할 수 있는 노드의 최대 개수는 다음과 같습니다.
$$2^{k-1}$$
레벨 k에서 Min Heap에 존재할 수 있는 노드의 최대 개수
= 레벨 k에서 Min Heap에 존재할 수 있는 노드의 최대 개수
= 레벨 k에 존재할 수 있는 노드의 최대 개수/2
$$= 2^{k-2}$$
즉 Min-Heap에 대응하는 Max-Heap의 위치는
$$j = i + 2^{[log_2(i)] + 1-2}$$
$$= i + 2^{[log_2(i)] - 1}$$
이때 j가 존재하지 않는 경우, 즉 j > n(노드의 수)인 경우
$$j = j/2$$
Man Heap에 대응하는 Min Heap의 요소 찾기
Max Heap에 속한 노드의 인덱스를 j라고 하겠습니다. 대응하는 Min Heap의 요소의 인덱스를 i라고 하면
$$i = j - 2^{[log_2(j)] - 1} $$
이때 Deap은 완전 이진 트리이므로 Max Heap에 대응하는 Min Heap의 요소는 항상 존재합니다.
위치가 주어졌을 때 Max Heap에 속하는지 여부 판단하기
위치 i가 속한 레벨을 k라 하면 다음과 같습니다.
$$k= [log_2(i)]+1$$
Max Heap에 속하는지의 여부는 다음과 같습니다.
$$i \geq 2^{k-1} + 2^{k-2}$$
이때 다음은 max heap에서의 최좌측 위치입니다.
$$ 2^{k-1} + 2^{k-2}$$
Deap에서의 삽입
1. 원소를 가장 마지막 위치에 삽입합니다.
2. 삽입된 위치가 Max Heap에 속하는지 Min Heap에 속하는지 확인합니다.
3. Min Heap에 속하는 경우 대응되는 Max Heap의 원소와 비교합니다.
(Max Heap에 속하는 경우 3,4,5번의 과정에서 Min과 Max를 반대로 진행합니다.)
4. Max Heap의 원소보다 작은 경우 삽입된 위치의 부모와 비교해가며 망가진 Min Heap을 복구합니다.
5. Max Heap의 원소보다 큰 경우 두 원소를 교체한 후, 교체한 Max Heap의 위치에서 망가진 Max Heap을 복구합니다
Max Heap에 삽입
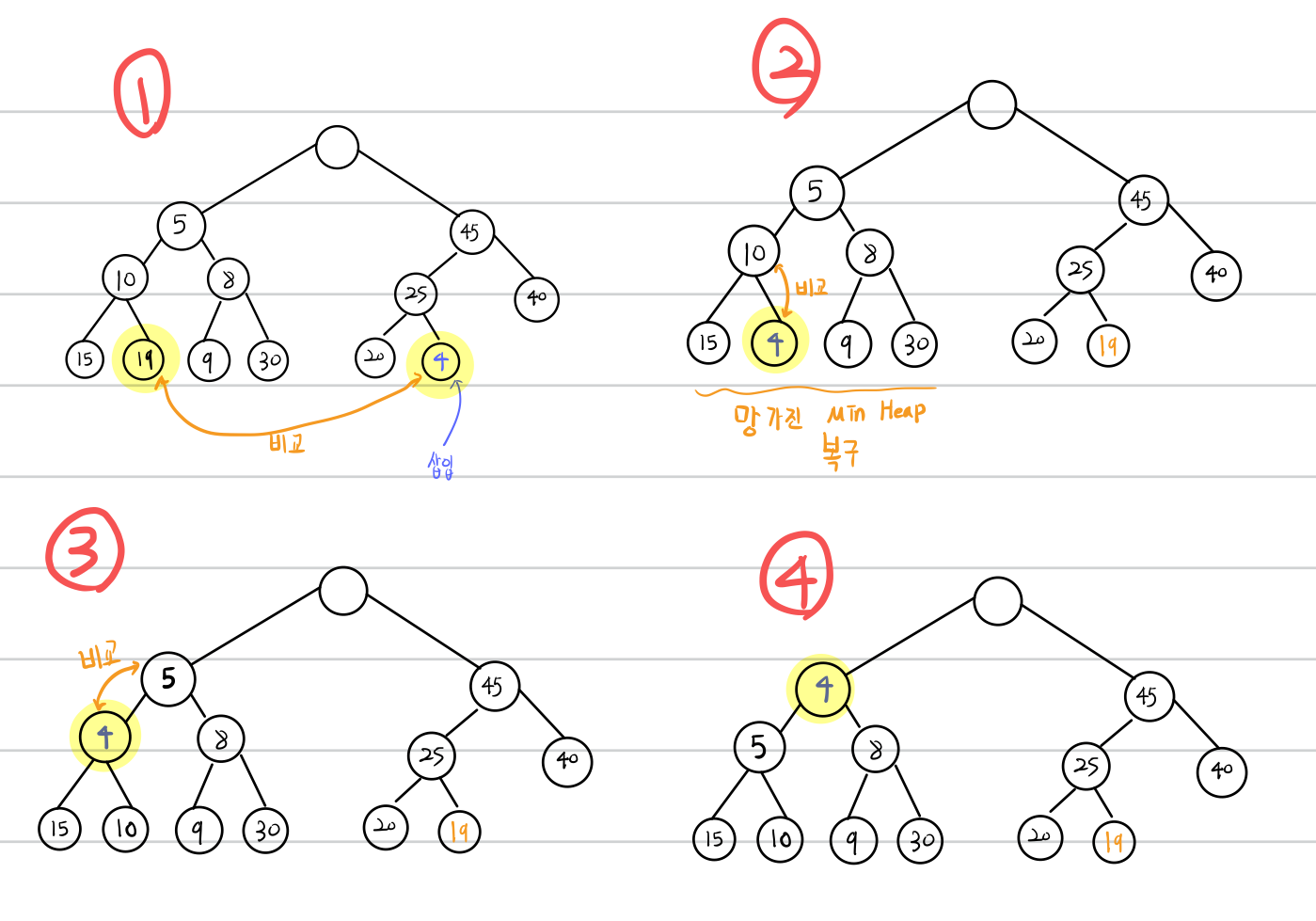
Min Heap에 삽입
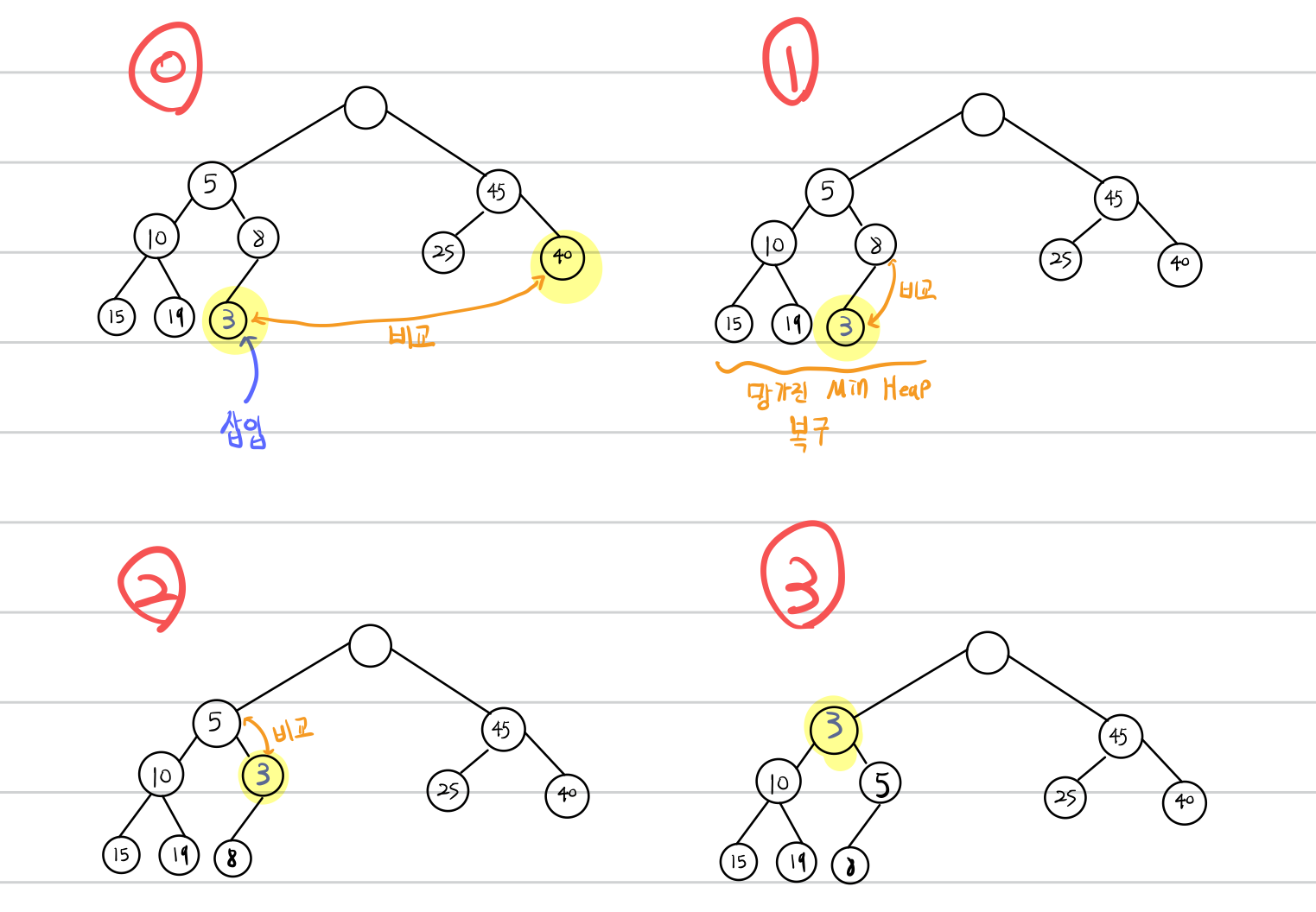
Deap에서의 최솟값 삭제
1. Min Heap의 루트를 제거합니다. 이 값이 최솟값입니다.
2. Min Heap의 루트로부터 시작하여 다음을 반복합니다.
3. 자식 노드를 확인합니다. 존재한다면 자식들 중 더 작은 값을 자신의 위치로 옮깁니다.
4. 이후 자신의 인덱스를 자식의 인덱스로 바꾸어줍니다.
5. 자식 노드가 존재하지 않는다면 반복을 종료합니다.
6. 반복을 종료한 뒤, 가장 마지막 노드를 마지막 위치 자리에서 제거하며, 현재 위치로 옮겨줍니다.
7. Deap이 망가졌으므로 복구를 진행해야 합니다.
아래는 복구하는 과정입니다.
9. 마지막 노드가 삽입된 현재 위치에서 대응되는 Max Heap의 원소와 비교합니다.
10. 현재 위치(Min Heap)의 원소가 Max Heap의 원소보다 크다면 이를 교체해준 후, 망가진 두 Heap을 복구합니다.(이는 삽입과 동일한 과정입니다.)
11. 현재 위치(Min Heap)의 원소가 Max Heap의 원소보다 작지 않다면 망가진 Min-Heap을 복구합니다.
예시 1
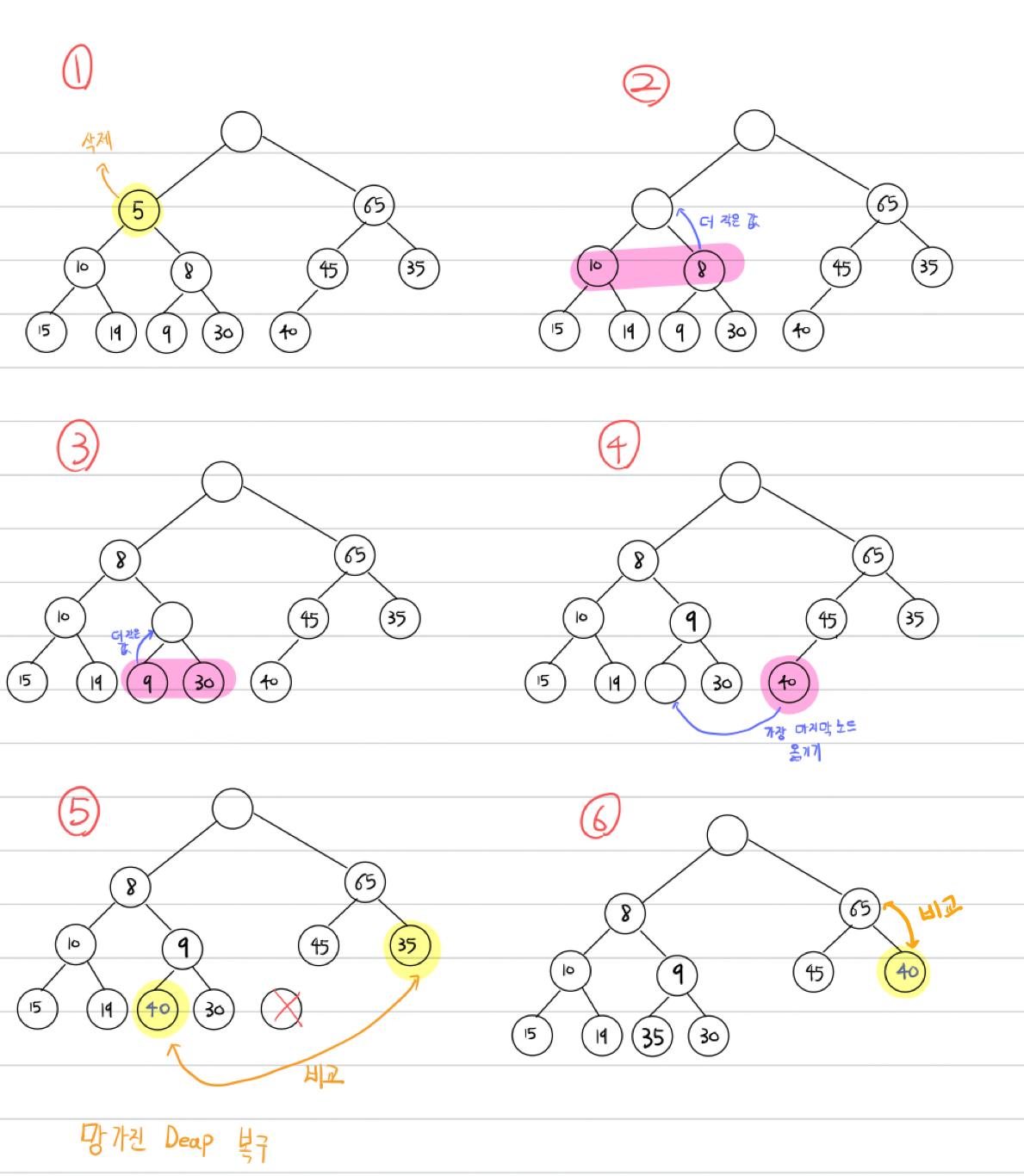
예시 2
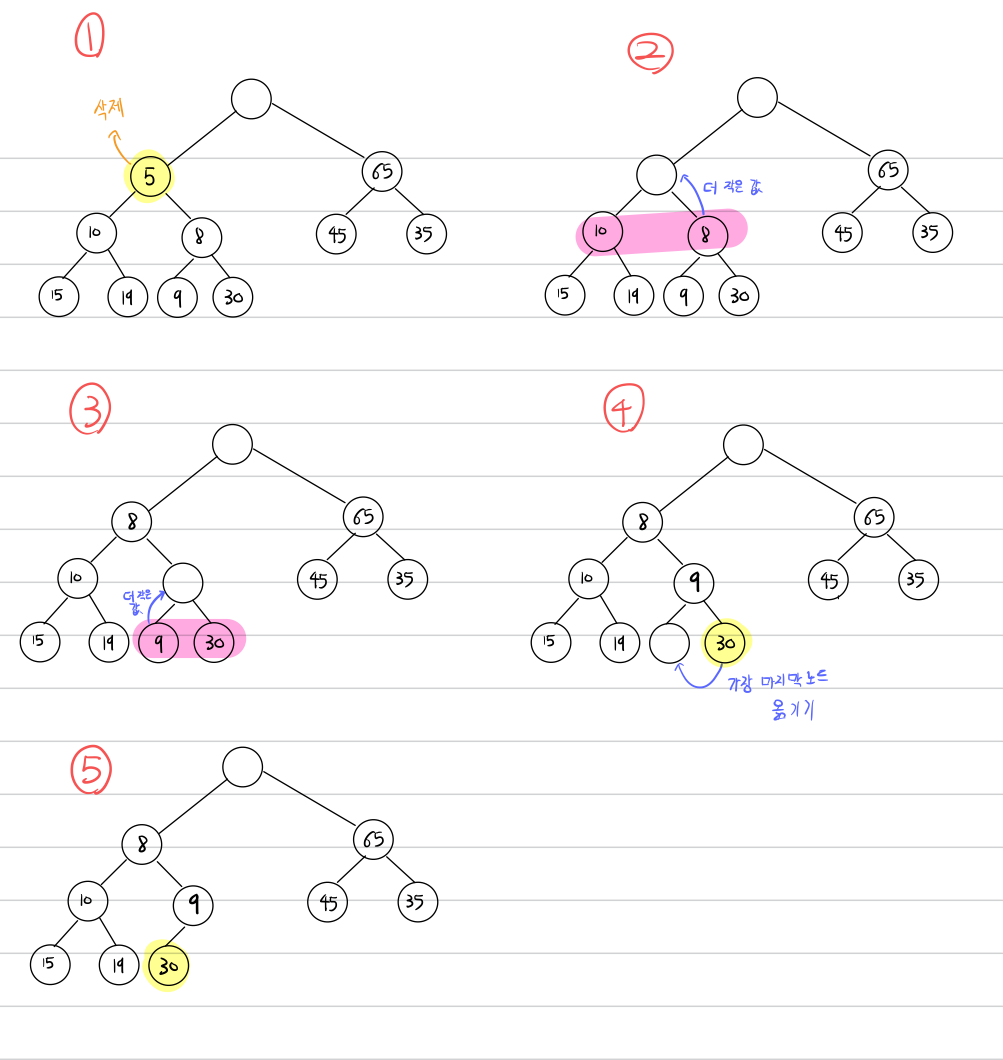
Deap에서의 최댓값 삭제
최솟값 삭제와 비슷합니다.
1. Max Heap의 루트를 제거합니다. 이 값이 최댓값입니다.
2. Max Heap의 루트로부터 시작하여 다음을 반복합니다.
3. 자식 노드를 확인합니다. 존재한다면 자식들 중 더 큰 값을 자신의 위치로 옮깁니다.
4. 이후 자신의 인덱스를 자식의 인덱스로 바꾸어줍니다.
5. 자식 노드가 존재하지 않는다면 반복을 종료합니다.
6. 반복을 종료한 뒤, 가장 마지막 노드를 마지막 위치 자리에서 제거하며, 현재 위치로 옮겨줍니다.
7. Deap이 망가졌으므로 복구를 진행해야 합니다.
아래는 복구하는 과정입니다.
9. 마지막 노드가 삽입된 현재 위치에서 대응되는 Min Heap의 원소와 비교합니다.
10. 현재 위치(Max Heap)의 원소가 Min Heap의 원소보다 크다면 이를 교체해준 후, 망가진 두 Heap을 복구합니다.(이는 삽입과 동일한 과정입니다.)
11. 현재 위치(Min Heap)의 원소가 Max Heap의 원소보다 작지 않다면 망가진 Min-Heap을 복구합니다.
시간복잡도
| 삽입 | 최댓값 삭제 | 최솟값 삭제 |
| $$Olog(n)$$ | $$Olog(n)$$ | $$Olog(n)$$ |
자바로 구현
https://ttl-blog.tistory.com/713
[Java] 자바로 Deap 구현하기
Deap이란? 더보기 https://ttl-blog.tistory.com/712 [자료구조] - 딥(Deap) Deap이란? 완전 이진 트리(Complete Binary Tree)이며, 비어있거나 다음을 만족시키는 자료구조입니다. 1. Root 노드는 아무런 요소를..
ttl-blog.tistory.com
'🖥 Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] - AVL 트리 (0) | 2022.06.09 |
|---|---|
| [자료구조] - Hash(해시) (0) | 2022.06.07 |
| [자료구조] - 우선순위 큐(Priority Queue) (0) | 2022.06.06 |
| [자료구조] - 힙(Heap) (0) | 2022.06.06 |
| [자료구조] - 이진 검색 트리 (Binary Search Tree - BST) (0) | 2022.06.05 |