문맥 자유 언어
문법 G = (V, T, S, P)에서 모든 생성규칙이
$$A \to x$$
의 형태를 가지면 G를 문맥-자유 문법(Context-free Grammer, CFG)이라 합니다.
이때 A와 x는 다음과 같습니다.
$$A \in V, \;\;\;\; x \in (V \cup T)^{*}$$
또한 언어 L에 대해서 L = L(G)를 만족하는 문맥-자유 문법 G가 존재하고, 오직 그럴 때에만 L을 문맥-자유 언어(Context-free Lanuage, CFL)라고 합니다.
위의 정의에 의하여 모든 정규 문법은 문맥 자유 문법이 되며
따라서 정규 언어는 문백 자유 언어임을 알 수 있습니다.
즉 정규 언어군은 문맥 자유 언어군의 진부분 집합입니다.
문맥 자유라는 이름은 문장 형태(sentencial form)에 있는 임의의 변수(Nonterminal Symbol)는 그 변수를 좌변으로 같은 생성규칙에 의하여 치환될 수 있으며
이때 이러한 치환은 문장 형태에 있는 나머지 심벌들과는 상관없이 이루어지기에 문맥에 자유롭다 하여 붙여진 이름입니다.
회문 (palindrome)
다음의 생성 규칙을 갖는 문법은 문맥 자유 문법입니다.
$$G = (\left\{ S \right\}, \left\{ a, b\right\}, S, P)$$
$$S \to aSa\; | \;bSb\; | \;\lambda$$
해당 문법으로 인해 유도되는 언어는 다음과 같습니다.
$$ S \Rightarrow aSa \Rightarrow aaSaa \Rightarrow aabSbaa \Rightarrow aabbaa $$
$$ S \Rightarrow bSb \Rightarrow baSab \Rightarrow baab$$
해당 문법에 의해 정의되는 언어는 다음과 같으며
$$L(G) = \left\{ ww^{R} \; : \; w \in \left\{ a, b \right\} \right\}$$
다음과 같이도 표현합니다.
even-length palindromes in { 𝑎, 𝑏 }*
좌측 우선 유도와 우측 우선 유도
선형 문법이 아닌 문맥 자유 문법에 대한 유도에서, 두 개 이상의 변수를 포함하고 있는 문장 형태가 나타날 수 있습니다.
이러한 경우에 여러 변수들을 어느 순서로 대체할 것인가 선택해야 합니다.
좌측우선 유도 : 유도 과정의 각 단계에서 각 문장 형태의 가장 좌측 변수가 대체되는 유도
우측우선 유도 : 가장 우측 변수가 대체되는 유도
유도 트리 (Derivation Trees)
유도 트리는 유도 과정을 보이는 방법으로 사용되는 수단입니다.
이 표현 방법은 사용된 생성규칙들의 순서와는 무관합니다.
유도 트리는 순서 트리로서 부모 노드는 생성규칙의 좌변에 있는 변수로 라벨이 주어지고, 이 노드의 자식 노드는 대응되는 우변에 있는 심벌들을 표현합니다.
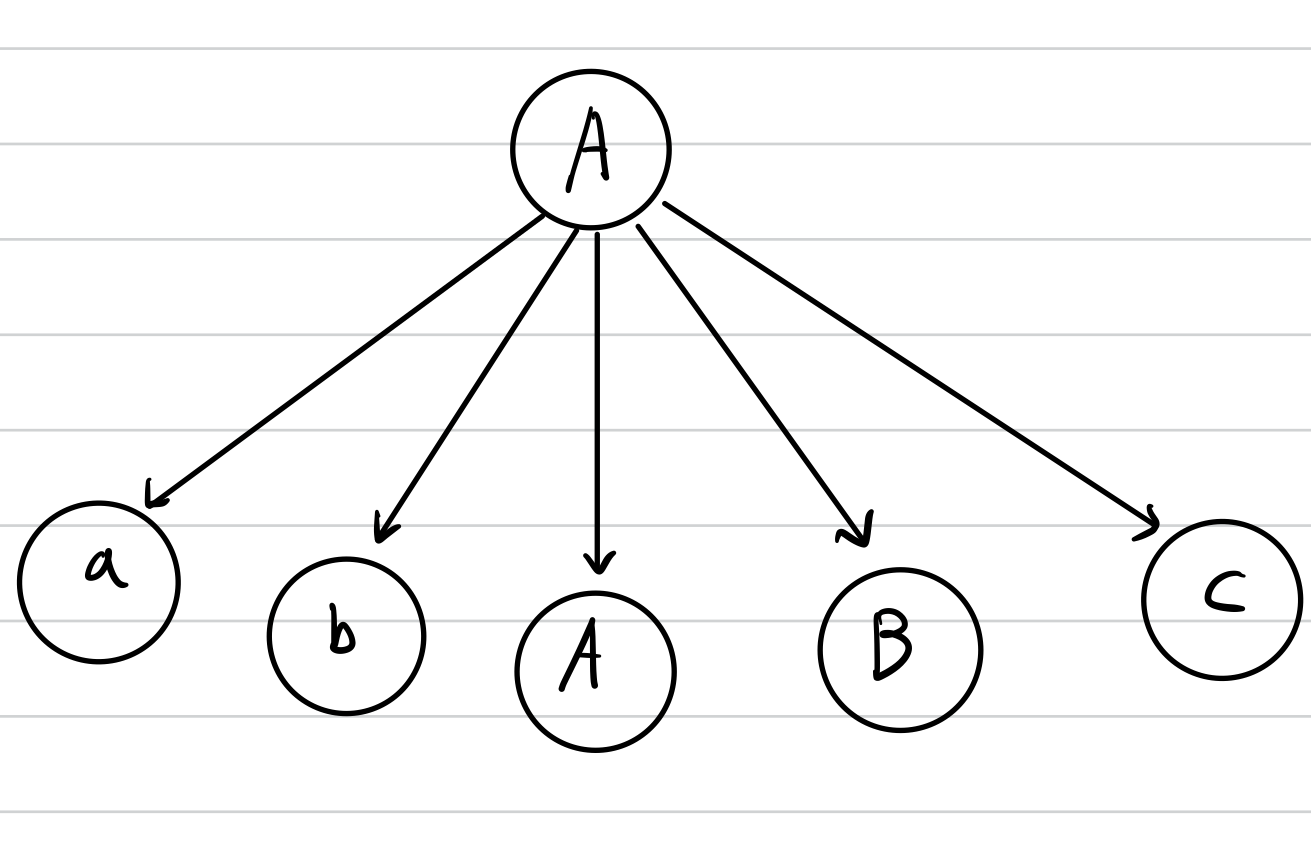
예를 들면 아래 그림은 다음의 생성규칙에 대한 유도 트리의 한 부분을 보여주고 있습니다.
$$A \to abABc$$
즉 유도 트리에서는 생성규칙의 좌변에 있는 변수를 라벨로 갖는 노드는 이 규칙의 우변에 있는 심벌들을 자식 노드들로 가지게 됩니다.
유도 트리의 정의는 다음과 같습니다.
G = (V, T, S, P)가 문맥 자유 문법이라 하면, 순서 트리가 G의 유도 트리가 되기 위한 필요충분조건은 다음과 같습니다.
1. 루트 노드의 라벨은 시작 변수 S입니다.
2. 각 리프 노드의 라벨은 $T \cup \left\{ \lambda \right\}$ 의 심벌입니다.
3. 각 내부 노드의 라벨은 V에 속한 변수입니다.
4. 만약 라벨이 $A \in V$ 인 노드가 라벨이 (왼쪽에서 오른쪽으로 차례로) $a_1, a_2, ..., a_n$ 인 자식 노드들을 갖는다면, P는 다음 형태의 생성규칙을 갖고 있어야 합니다.
$$A \to a_1 a_2 ... a_n$$
5. 라벨이 $\lambda$ 인 자식 노드는 형제 노드가 없습니다.
즉 라벨이 $\lambda$ 인 자식 노드를 갖는, $\lambda$ 노드의 부모 노드는 다른 자식들을 가질 수 없습니다.
트리가 위의 조건들 중에서 3, 4, 5를 항상 만족하며, 1은 반드시 만족할 필요가 없고,
조건 2 대신 다음 조건을 만족하는 경우, 이 트리를 부분 유도 트리(partial derivation tree)라고 합니다.
- 모든 잎 노드는 $( V \cup T \cup \left\{ \lambda \right\} )$ 의 표식을 갖습니다.
유도 트리의 생성물(yeild)은 유도트리의 잎 노드를 왼쪽에서부터 오른쪽으로 차례로 읽어서 얻어진 심벌들의 문자열을 의미합니다.
문장 형태와 유도 트리와의 관계
$G = (V, T, S, P)$ 를 문맥 - 자유 문법이라 할 때, 모든 $w \in L(G)$ 에 대하여, 생성물이 w인 G의 유도 트리가 존재합니다.
역으로 모든 유도 트리의 생성물은 L(G)에 속합니다.
t가 루트 노드가 S인 G의 부분 유도 트리이면, t의 생성물은 G의 문장 형태입니다.
'🖥 Computer Science > 계산이론' 카테고리의 다른 글
| [계산이론] - (12) 문맥 자유 문법의 단순화 (2) | 2022.05.26 |
|---|---|
| [계산이론] - (11) 파싱과 모호성(Parsing, Ambiguity) (0) | 2022.05.26 |
| [계산이론] - (9) 펌핑 보조정리 (Pumping lemma) (0) | 2022.05.22 |
| [계산이론] - (8) 비정규 언어의 식별 (0) | 2022.05.22 |
| [계산이론] - (7) 정규 언어의 폐포(Closure) 성질 (0) | 2022.05.11 |
문맥 자유 언어
문법 G = (V, T, S, P)에서 모든 생성규칙이
A→xA→x
의 형태를 가지면 G를 문맥-자유 문법(Context-free Grammer, CFG)이라 합니다.
이때 A와 x는 다음과 같습니다.
A∈V,x∈(V∪T)∗A∈V,x∈(V∪T)∗
또한 언어 L에 대해서 L = L(G)를 만족하는 문맥-자유 문법 G가 존재하고, 오직 그럴 때에만 L을 문맥-자유 언어(Context-free Lanuage, CFL)라고 합니다.
위의 정의에 의하여 모든 정규 문법은 문맥 자유 문법이 되며
따라서 정규 언어는 문백 자유 언어임을 알 수 있습니다.
즉 정규 언어군은 문맥 자유 언어군의 진부분 집합입니다.
문맥 자유라는 이름은 문장 형태(sentencial form)에 있는 임의의 변수(Nonterminal Symbol)는 그 변수를 좌변으로 같은 생성규칙에 의하여 치환될 수 있으며
이때 이러한 치환은 문장 형태에 있는 나머지 심벌들과는 상관없이 이루어지기에 문맥에 자유롭다 하여 붙여진 이름입니다.
회문 (palindrome)
다음의 생성 규칙을 갖는 문법은 문맥 자유 문법입니다.
G=({S},{a,b},S,P)G=({S},{a,b},S,P)
S→aSa|bSb|λS→aSa|bSb|λ
해당 문법으로 인해 유도되는 언어는 다음과 같습니다.
S⇒aSa⇒aaSaa⇒aabSbaa⇒aabbaaS⇒aSa⇒aaSaa⇒aabSbaa⇒aabbaa
S⇒bSb⇒baSab⇒baabS⇒bSb⇒baSab⇒baab
해당 문법에 의해 정의되는 언어는 다음과 같으며
L(G)={wwR:w∈{a,b}}L(G)={wwR:w∈{a,b}}
다음과 같이도 표현합니다.
even-length palindromes in { 𝑎, 𝑏 }*
좌측 우선 유도와 우측 우선 유도
선형 문법이 아닌 문맥 자유 문법에 대한 유도에서, 두 개 이상의 변수를 포함하고 있는 문장 형태가 나타날 수 있습니다.
이러한 경우에 여러 변수들을 어느 순서로 대체할 것인가 선택해야 합니다.
좌측우선 유도 : 유도 과정의 각 단계에서 각 문장 형태의 가장 좌측 변수가 대체되는 유도
우측우선 유도 : 가장 우측 변수가 대체되는 유도
유도 트리 (Derivation Trees)
유도 트리는 유도 과정을 보이는 방법으로 사용되는 수단입니다.
이 표현 방법은 사용된 생성규칙들의 순서와는 무관합니다.
유도 트리는 순서 트리로서 부모 노드는 생성규칙의 좌변에 있는 변수로 라벨이 주어지고, 이 노드의 자식 노드는 대응되는 우변에 있는 심벌들을 표현합니다.
예를 들면 아래 그림은 다음의 생성규칙에 대한 유도 트리의 한 부분을 보여주고 있습니다.
A→abABcA→abABc
즉 유도 트리에서는 생성규칙의 좌변에 있는 변수를 라벨로 갖는 노드는 이 규칙의 우변에 있는 심벌들을 자식 노드들로 가지게 됩니다.

유도 트리의 정의는 다음과 같습니다.
G = (V, T, S, P)가 문맥 자유 문법이라 하면, 순서 트리가 G의 유도 트리가 되기 위한 필요충분조건은 다음과 같습니다.
1. 루트 노드의 라벨은 시작 변수 S입니다.
2. 각 리프 노드의 라벨은 T∪{λ}T∪{λ} 의 심벌입니다.
3. 각 내부 노드의 라벨은 V에 속한 변수입니다.
4. 만약 라벨이 A∈VA∈V 인 노드가 라벨이 (왼쪽에서 오른쪽으로 차례로) a1,a2,...,ana1,a2,...,an 인 자식 노드들을 갖는다면, P는 다음 형태의 생성규칙을 갖고 있어야 합니다.
A→a1a2...anA→a1a2...an
5. 라벨이 λλ 인 자식 노드는 형제 노드가 없습니다.
즉 라벨이 λλ 인 자식 노드를 갖는, λλ 노드의 부모 노드는 다른 자식들을 가질 수 없습니다.
트리가 위의 조건들 중에서 3, 4, 5를 항상 만족하며, 1은 반드시 만족할 필요가 없고,
조건 2 대신 다음 조건을 만족하는 경우, 이 트리를 부분 유도 트리(partial derivation tree)라고 합니다.
- 모든 잎 노드는 (V∪T∪{λ})(V∪T∪{λ}) 의 표식을 갖습니다.
유도 트리의 생성물(yeild)은 유도트리의 잎 노드를 왼쪽에서부터 오른쪽으로 차례로 읽어서 얻어진 심벌들의 문자열을 의미합니다.
문장 형태와 유도 트리와의 관계
G=(V,T,S,P)G=(V,T,S,P) 를 문맥 - 자유 문법이라 할 때, 모든 $w \in L(G)$ 에 대하여, 생성물이 w인 G의 유도 트리가 존재합니다.
역으로 모든 유도 트리의 생성물은 L(G)에 속합니다.
t가 루트 노드가 S인 G의 부분 유도 트리이면, t의 생성물은 G의 문장 형태입니다.
'🖥 Computer Science > 계산이론' 카테고리의 다른 글
| [계산이론] - (12) 문맥 자유 문법의 단순화 (2) | 2022.05.26 |
|---|---|
| [계산이론] - (11) 파싱과 모호성(Parsing, Ambiguity) (0) | 2022.05.26 |
| [계산이론] - (9) 펌핑 보조정리 (Pumping lemma) (0) | 2022.05.22 |
| [계산이론] - (8) 비정규 언어의 식별 (0) | 2022.05.22 |
| [계산이론] - (7) 정규 언어의 폐포(Closure) 성질 (0) | 2022.05.11 |