서론
저희는 지금까지 정규 언어가 무엇인지에 대해서 배웠고,
정규 언어를 표현하기 위해 정규 표현, 유한 오토마타와 정규 문법을 배웠으며
이들 상호간에 변환하는 방법을 알아보았습니다.
지금부터는 모든 정규 언어들이 가지는 성질에 대해 알아보고자 합니다.
정규 언어들에 합집합, 교집합 등의 연산을 취해 생성되는 새로운 언어들은 어떤 특징들을 가지는지,
어떤 언어가 정규 언어인지 아닌지를 어떻게 보일 수 있는지에 대해 알아보겠습니다.
모든 형식 언어(formal language)는 정규 언어가 아닙니다.
이를 증명하기 위해 정규 언어의 특성을 깊이 이해하고 정규 언어를 포함하는 전체 언어들이 어떠한 성질을 가지고 있는지를 확인해야 합니다.
저희는 앞으로 다음 질문들에 대한 해답을 찾아갈 것입니다.
정규 언어에 연산을 취할 경우 그 결과는 정규 언어인가
주어진 언어의 정규 언어 여부 판정을 할 수 있는가
우선 '정규 언어에 연산을 취할 경우 그 결과는 정규 언어인가'에 대한 의문을 해결해 보도록 하겠습니다.
이러한 질문은 폐포(closue)성질을 묻는 질문입니다.
수학에서, 어떤 집합의 그 위의 관계에 대한 닫힘(영어: closure)은 그 집합의 원소와 관계가 있는 원소가 항상 그 집합에 속한다는 성질이다.
어떤 집합의 어떤 성질에 대한 폐포(閉包, 영어: closure)는 그 집합을 포함하면서 그 성질을 만족시키는 가장 작은 대상이다. 여기서 다루는 성질은 보통 닫힘 성질이다.
위키백과 - https://ko.wikipedia.org/wiki/%ED%8F%90%ED%8F%AC_(%EC%88%98%ED%95%99)
정규 언어의 폐포 성질
두개의 정규 언어 L1과 L2에 대해 이들의 합집합은 정규 표현입니다.
이는 모든 정규 언어들에 대해 성립하며, 따라서 다음과 같이 표현합니다.
정규 언어군(family of regular languages)은 합집합에 대해 폐포(clodsed)되어 있다고 표현합니다.
합집합 뿐만 아니라, 다른 연산들에 대해서도 연산의 결과가 정규 언어인지에 대한 질문들의 답을 구하는 것이 정규 언어의 일반적인 폐포 성질을 찾아가는 것입니다.
간단한 집합 연산에 대한 폐포 성질
정규언어 $L_1$과 $L_2$가 있을 때, 아래의 연산 결과 역시 정규 언어입니다.
$$L_1 \cup L_2,\;\;L_1 \cap L_2, \;\; L_1L_2 ,\;\; \overline{L_1} ,\;\; L_1^{*}, \;\; L_1^R$$
즉 정규 언어는 합집합, 교집합, 접합, 여집합, 스타-폐포, 역(reverse)에 대해 모두 폐포 성질이 성립합니다.
간단한 증명은 다음과 같습니다.
$L_1$과 $L_2$ 가 정규 언어인 경우, $L_1 = (r_1)$ 과 $L_2=(r_2)$ 를 만족하는 정규 표현 $r_1$ 와$r_2$ 가 존재함은 자명합니다.
$$r_1+r_2 \;\; r_1r_2 \;\; r^{*}$$
위의 연산의 결과로 나오는 정규 표현들은 각각 $L_1$ 과 $L_2$ 의 합집합, 접합, 스타-폐포 연산을 표현하는 정규 표현이며, 따라서 이들 연산에 대한 폐포(closed) 성질이 바로 성립합니다.
여집합에 대한 폐포 성질은 다음과 같이 구합니다.
dfa의 정의에서 $\delta^{*}$ 가 전체 함수(total function)이었습니다.
즉 dfa의 알파벳(terminal-symbol)의 스타-폐포 연산으로 인해 만들어지는 문자열(string)에 대해,
확장 전이 함수 $\delta^{*}$ 가 정의됩니다.
$$w \in L \;\; \delta^{*}(q_0, w)$$
$$w \in \overline{L} \;\; \delta^{*}(q_0, w) \in Q - F$$
즉 여집합에 대한 폐포 성질도 성립합니다.
나머지 성질들에 대해서도 증명할 수 있으나, 생략하고 다음으로 넘어가도록 하겠습니다.
지금부터는 기타 연산들 중 2가지(준동형, 우측 몫)에 대한 정규 언어의 폐포 성질에 대해 알아보도록 하겠습니다.
준동형(homomorphism)
$\Sigma$ 와 $\Gamma$ 가 알파벳이라 하면, 다음과 같이 정의된 함수 h를 준동형이라고 합니다.
$$h : \;\; \Sigma \to \Gamma$$
쉽게 말하면, 준동형은 단일 심벌(terminal symbol)을 문자열로 치환(substitution)하는 함수입니다.
또한 $L $ 이 $ \Sigma $ 에 대한 언어이면, $L$ 의 준동형 상(homomorphic image)은 다음과 같이 정의됩니다.
$$h(L) = \left\{ h(w) : w \in L \right\} $$
정규 언어군은 임의의 준동형에 대해 폐포 성질이 성립합니다.
준동형에 대한 예시입니다.
$$\Sigma = \left\{ a, b \right\} \;\;\; \Gamma = \left\{ a, b, c \right\}$$
이때 h를 다음과 같이 정의합니다.
$$h(a) = ab, \;\;h(b) = bbc$$
위 준동형 함수를 문자열 aba에 사용하면 다음과 같습니다.
$$h(aba)=abbbcab$$
또한 다음 언어 L의 준동형 상은
$$ L = \left\{ aa, aba \right\} $$
$$h(L) = \left\{ abab, abbbcab \right\}$$
증명은 생략하겠습니다.
우측 몫(right quotient)
$L_1$ 과 $L_2$ 가 동일한 알파벳에 대한 정규 언어일 때, $L_2$ 에 대한 $L_1$ 의 우측 몫(right quotient)의 정의는 다음과 같습니다.
$$L_1 / L_2 = \left\{ x\;:\; xy \in L_1 \;\; for\;\;some\;\; y \in L_2 \right\}$$
$L_2$ 에 대한 $L_1$의 우측 몫을 구성하기 위하여
$L_2$ 에 속하는 문자열을 후위부(suffix)로 갖는 $L_1$ 에 속한 모든 문자열을 모야 합니다.
이후 문자열에서 후위부를 제거하거 남은 문자열이 $L_1/L_2$ 에 속하게 됩니다.
예시는 다음과 같습니다.
$$L_1 = \left\{ a^{n}b^{m} \; : \; n\geq 1 m \geq 0 \right\} \cup \left\{ ba \right\}$$
$$L_2 = \left\{ b^{m} : m \geq 1 \right\}$$
위와 같이 정의된 언어 $L_1$ 과 $L_2$ 에 대해, $L_1/L_2$ 는 다음과 같습니다.
$$L_1 / L_2 \left\{ a^{n}b^{m} \; : \; n \geq 1, m \geq 0 \right\}$$
정규 언어군은 우측 몫 연산에 대해 폐포 성질이 성립합니다. 증명은 생략하겠습니다.
우측 몫을 구하는 방법
$L_2$ 에 대한 $L_1$ 의 우측 몫( $L_1$ / $L_2$ )을 구하는 방법은 다음과 같습니다.
1. $L_1$ 에 대한 d.f.a를 구성합니다.
2. 해당 d.f.a의 모든 state들에 대해, $L_2$ 에 속한 문자열을 적용하여 final state로 갈 수 있는 state들을 모두 final state로 바꿉니다
이때 $L_2$ 에 속한 모든 문자열에 대해 final state로 갈 필요는 없습니다.
3. 우측 몫의 정의에 따라, $L_2$에 속한 문자열들 중 단 하나라도 적용되어 final state로 향할 수 있다면 이는 가능한 것입니다.
4. 바뀐 d.f.a가 인식하는 문자열이 $L_2$ 에 대한 $L_1$ 의 우측 몫( $L_1/L_2$ )입니다.
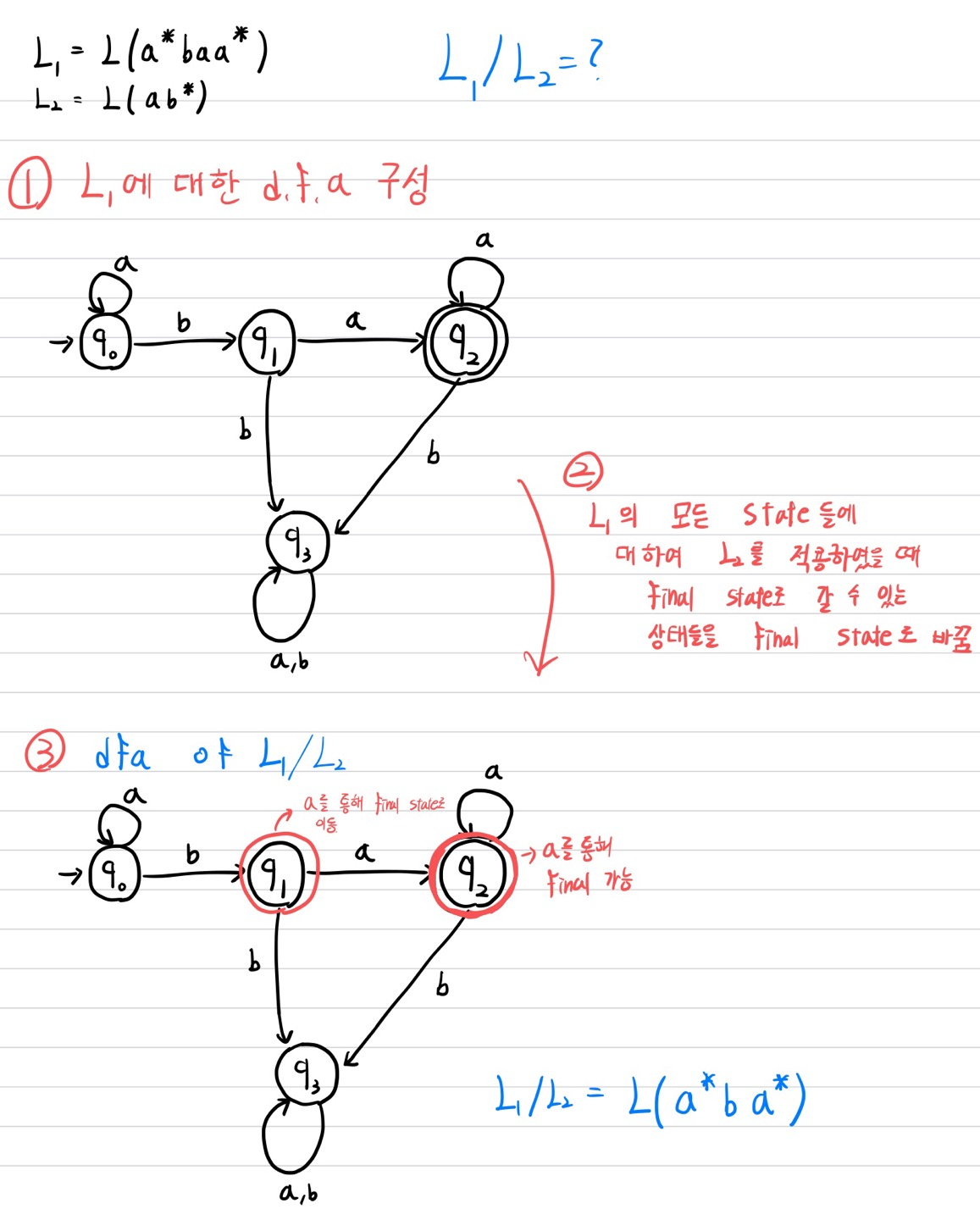
예시)
'🖥 Computer Science > 계산이론' 카테고리의 다른 글
| [계산이론] - (9) 펌핑 보조정리 (Pumping lemma) (0) | 2022.05.22 |
|---|---|
| [계산이론] - (8) 비정규 언어의 식별 (0) | 2022.05.22 |
| [계산이론] - (6) 정규 문법(regular grammer) (2) | 2022.05.11 |
| [계산이론] - (5) 정규 표현 (Regular Expression) (0) | 2022.05.04 |
| [계산이론] - (4) 밀리기계(Mealy Machine), 무어기계(Moore Machine) (0) | 2022.04.25 |
서론
저희는 지금까지 정규 언어가 무엇인지에 대해서 배웠고,
정규 언어를 표현하기 위해 정규 표현, 유한 오토마타와 정규 문법을 배웠으며
이들 상호간에 변환하는 방법을 알아보았습니다.
지금부터는 모든 정규 언어들이 가지는 성질에 대해 알아보고자 합니다.
정규 언어들에 합집합, 교집합 등의 연산을 취해 생성되는 새로운 언어들은 어떤 특징들을 가지는지,
어떤 언어가 정규 언어인지 아닌지를 어떻게 보일 수 있는지에 대해 알아보겠습니다.
모든 형식 언어(formal language)는 정규 언어가 아닙니다.
이를 증명하기 위해 정규 언어의 특성을 깊이 이해하고 정규 언어를 포함하는 전체 언어들이 어떠한 성질을 가지고 있는지를 확인해야 합니다.
저희는 앞으로 다음 질문들에 대한 해답을 찾아갈 것입니다.
정규 언어에 연산을 취할 경우 그 결과는 정규 언어인가
주어진 언어의 정규 언어 여부 판정을 할 수 있는가
우선 '정규 언어에 연산을 취할 경우 그 결과는 정규 언어인가'에 대한 의문을 해결해 보도록 하겠습니다.
이러한 질문은 폐포(closue)성질을 묻는 질문입니다.
수학에서, 어떤 집합의 그 위의 관계에 대한 닫힘(영어: closure)은 그 집합의 원소와 관계가 있는 원소가 항상 그 집합에 속한다는 성질이다.
어떤 집합의 어떤 성질에 대한 폐포(閉包, 영어: closure)는 그 집합을 포함하면서 그 성질을 만족시키는 가장 작은 대상이다. 여기서 다루는 성질은 보통 닫힘 성질이다.
위키백과 - https://ko.wikipedia.org/wiki/%ED%8F%90%ED%8F%AC_(%EC%88%98%ED%95%99)
정규 언어의 폐포 성질
두개의 정규 언어 L1과 L2에 대해 이들의 합집합은 정규 표현입니다.
이는 모든 정규 언어들에 대해 성립하며, 따라서 다음과 같이 표현합니다.
정규 언어군(family of regular languages)은 합집합에 대해 폐포(clodsed)되어 있다고 표현합니다.
합집합 뿐만 아니라, 다른 연산들에 대해서도 연산의 결과가 정규 언어인지에 대한 질문들의 답을 구하는 것이 정규 언어의 일반적인 폐포 성질을 찾아가는 것입니다.
간단한 집합 연산에 대한 폐포 성질
정규언어 $L_1$과 $L_2$가 있을 때, 아래의 연산 결과 역시 정규 언어입니다.
$$L_1 \cup L_2,\;\;L_1 \cap L_2, \;\; L_1L_2 ,\;\; \overline{L_1} ,\;\; L_1^{*}, \;\; L_1^R$$
즉 정규 언어는 합집합, 교집합, 접합, 여집합, 스타-폐포, 역(reverse)에 대해 모두 폐포 성질이 성립합니다.
간단한 증명은 다음과 같습니다.
$L_1$과 $L_2$ 가 정규 언어인 경우, $L_1 = (r_1)$ 과 $L_2=(r_2)$ 를 만족하는 정규 표현 $r_1$ 와$r_2$ 가 존재함은 자명합니다.
$$r_1+r_2 \;\; r_1r_2 \;\; r^{*}$$
위의 연산의 결과로 나오는 정규 표현들은 각각 $L_1$ 과 $L_2$ 의 합집합, 접합, 스타-폐포 연산을 표현하는 정규 표현이며, 따라서 이들 연산에 대한 폐포(closed) 성질이 바로 성립합니다.
여집합에 대한 폐포 성질은 다음과 같이 구합니다.
dfa의 정의에서 $\delta^{*}$ 가 전체 함수(total function)이었습니다.
즉 dfa의 알파벳(terminal-symbol)의 스타-폐포 연산으로 인해 만들어지는 문자열(string)에 대해,
확장 전이 함수 $\delta^{*}$ 가 정의됩니다.
$$w \in L \;\; \delta^{*}(q_0, w)$$
$$w \in \overline{L} \;\; \delta^{*}(q_0, w) \in Q - F$$
즉 여집합에 대한 폐포 성질도 성립합니다.
나머지 성질들에 대해서도 증명할 수 있으나, 생략하고 다음으로 넘어가도록 하겠습니다.
지금부터는 기타 연산들 중 2가지(준동형, 우측 몫)에 대한 정규 언어의 폐포 성질에 대해 알아보도록 하겠습니다.
준동형(homomorphism)
$\Sigma$ 와 $\Gamma$ 가 알파벳이라 하면, 다음과 같이 정의된 함수 h를 준동형이라고 합니다.
$$h : \;\; \Sigma \to \Gamma$$
쉽게 말하면, 준동형은 단일 심벌(terminal symbol)을 문자열로 치환(substitution)하는 함수입니다.
또한 $L $ 이 $ \Sigma $ 에 대한 언어이면, $L$ 의 준동형 상(homomorphic image)은 다음과 같이 정의됩니다.
$$h(L) = \left\{ h(w) : w \in L \right\} $$
정규 언어군은 임의의 준동형에 대해 폐포 성질이 성립합니다.
준동형에 대한 예시입니다.
$$\Sigma = \left\{ a, b \right\} \;\;\; \Gamma = \left\{ a, b, c \right\}$$
이때 h를 다음과 같이 정의합니다.
$$h(a) = ab, \;\;h(b) = bbc$$
위 준동형 함수를 문자열 aba에 사용하면 다음과 같습니다.
$$h(aba)=abbbcab$$
또한 다음 언어 L의 준동형 상은
$$ L = \left\{ aa, aba \right\} $$
$$h(L) = \left\{ abab, abbbcab \right\}$$
증명은 생략하겠습니다.
우측 몫(right quotient)
$L_1$ 과 $L_2$ 가 동일한 알파벳에 대한 정규 언어일 때, $L_2$ 에 대한 $L_1$ 의 우측 몫(right quotient)의 정의는 다음과 같습니다.
$$L_1 / L_2 = \left\{ x\;:\; xy \in L_1 \;\; for\;\;some\;\; y \in L_2 \right\}$$
$L_2$ 에 대한 $L_1$의 우측 몫을 구성하기 위하여
$L_2$ 에 속하는 문자열을 후위부(suffix)로 갖는 $L_1$ 에 속한 모든 문자열을 모야 합니다.
이후 문자열에서 후위부를 제거하거 남은 문자열이 $L_1/L_2$ 에 속하게 됩니다.
예시는 다음과 같습니다.
$$L_1 = \left\{ a^{n}b^{m} \; : \; n\geq 1 m \geq 0 \right\} \cup \left\{ ba \right\}$$
$$L_2 = \left\{ b^{m} : m \geq 1 \right\}$$
위와 같이 정의된 언어 $L_1$ 과 $L_2$ 에 대해, $L_1/L_2$ 는 다음과 같습니다.
$$L_1 / L_2 \left\{ a^{n}b^{m} \; : \; n \geq 1, m \geq 0 \right\}$$
정규 언어군은 우측 몫 연산에 대해 폐포 성질이 성립합니다. 증명은 생략하겠습니다.
우측 몫을 구하는 방법
$L_2$ 에 대한 $L_1$ 의 우측 몫( $L_1$ / $L_2$ )을 구하는 방법은 다음과 같습니다.
1. $L_1$ 에 대한 d.f.a를 구성합니다.
2. 해당 d.f.a의 모든 state들에 대해, $L_2$ 에 속한 문자열을 적용하여 final state로 갈 수 있는 state들을 모두 final state로 바꿉니다
이때 $L_2$ 에 속한 모든 문자열에 대해 final state로 갈 필요는 없습니다.
3. 우측 몫의 정의에 따라, $L_2$에 속한 문자열들 중 단 하나라도 적용되어 final state로 향할 수 있다면 이는 가능한 것입니다.
4. 바뀐 d.f.a가 인식하는 문자열이 $L_2$ 에 대한 $L_1$ 의 우측 몫( $L_1/L_2$ )입니다.
예시)

'🖥 Computer Science > 계산이론' 카테고리의 다른 글
| [계산이론] - (9) 펌핑 보조정리 (Pumping lemma) (0) | 2022.05.22 |
|---|---|
| [계산이론] - (8) 비정규 언어의 식별 (0) | 2022.05.22 |
| [계산이론] - (6) 정규 문법(regular grammer) (2) | 2022.05.11 |
| [계산이론] - (5) 정규 표현 (Regular Expression) (0) | 2022.05.04 |
| [계산이론] - (4) 밀리기계(Mealy Machine), 무어기계(Moore Machine) (0) | 2022.04.25 |