중심극한정리
모집단(Population)이 평균 $\mu$, 분산 $\sigma^2$ 인 임의의 분포를 이룰 때,
이 모집단으로부터 추출된 표본들에 대해서 표본의 크기 n이 충분히 크다면
표본평균은 다음 정규 분포에 수렴한다는 정리입니다.
$$\overline{X_n} \; \sim \; N(\;\mu, \; \frac{\sigma^{2}}{n}\; )$$
린데베르그-레비(Lindeberg and Levy) 중심극한정리
다음과 같이 정의됩니다.
평균 $\mu$, 분산 $\sigma^2$ 를 가지는 모집단으로부터 임의추출한 n개의 표본들에 있을 때, 표본평균은 모든 실수 x에 대해 다음이 성립합니다.
$$\displaystyle \lim_{ n\to \infty} P\left ( \frac{\overline{X_n}-\mu}{\frac{\sigma}{\sqrt{n}}} \leq x \right ) = \Phi(x)$$
이는 다음과 같이 작성할 수 있습니다.
$$\displaystyle \lim_{ n\to \infty} P\left ( \frac{\sqrt{n}\;(\overline{X_n}-\mu)\;}{\sigma} \leq x \right ) = \Phi(x)$$
$$\therefore \;\; \sqrt{n}(\overline{X_n} - \mu)\; \sim \; N(\;0, \sigma^{2})$$
$$\therefore \;\; (\overline{X_n} - \mu) \; \sim \; N(\;0, \frac{\sigma^{2}}{n})$$
$$\therefore \;\; \overline{X_n} \; \sim \; N(\;\mu, \frac{\sigma^{2}}{n})$$
즉 해석은 다음과 같습니다.
1) Sample mean(표본평균)은 평균이 $\mu$, 분산 $\frac{\sigma^{2}}{n}$ 인 Normal distribution으로 수렴(converge)한다.
2) 표본들의 합(X_1+ X_2+ ... + X_n)은 평균이 $n\mu$, 분산 $n\sigma^{2}$인 Normal distribution으로 수렴(converge)한다.
(표본평균 = 표본들의 합 / n(표본들의 개수))
이는 finite Variance가 아니어도 성립하며,
i.i.d는 충분조건이지 필요조건이 아닙니다.
(independent는 필요하지만, identically distributed는 충분조건입니다.
Lyapunov central limit theorem에서는 i.d가 아닌 경우에도 성립합니다.)
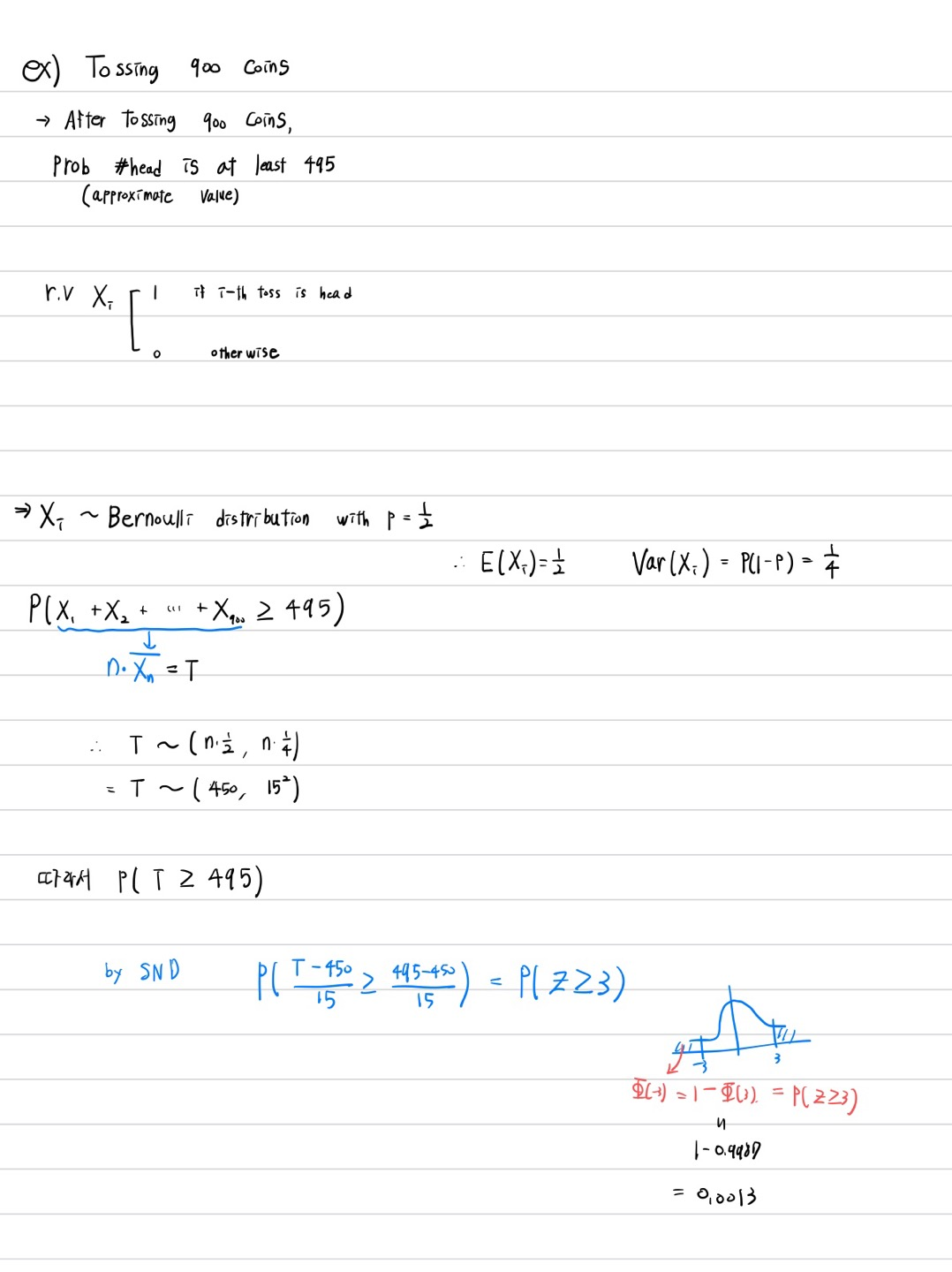
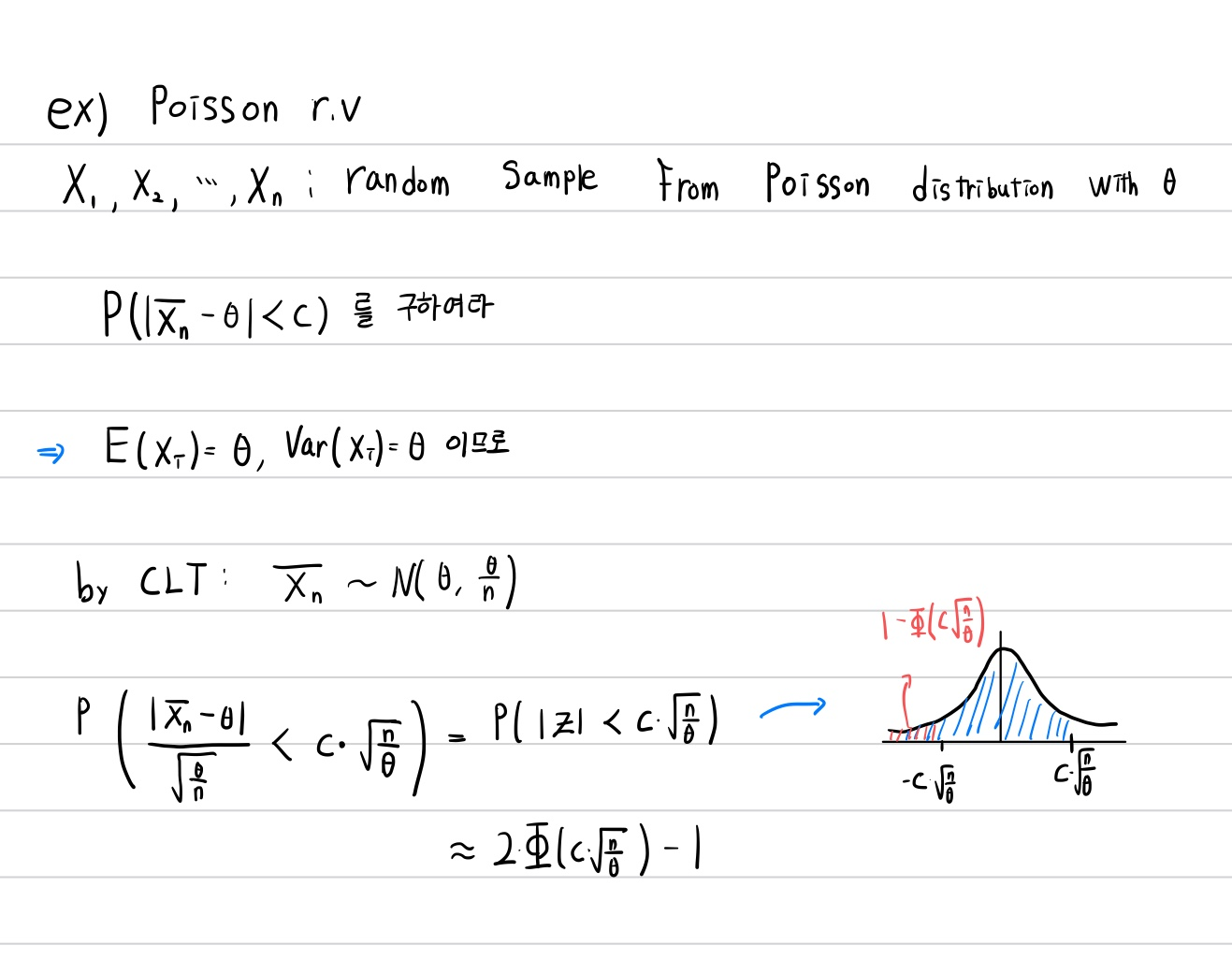
예시)
구간 [a , b]에서 Uniform Distribution의 p.d.f
$$f(x) = \left\{\begin{matrix} \frac{1}{b-a} & (a \leq x \leq b)\\ 0 & otherwise \\ \end{matrix}\right.$$
$$Var(X) = \frac{(b-a)^{2}}{12}$$

참고
https://math.stackexchange.com/questions/920661/clt-infinite-variance
CLT - infinite variance
Student t distribution with df=2 has infinite variance => CLT should not hold(?) Yet, when I draw a large sample thousands of times and plot the histogram of the standardized sample mean, it has a ...
math.stackexchange.com
https://drhongdatanote.tistory.com/57
[개념 통계 17] 중심극한 정리는 무엇이고 왜 중요한가?
안녕하세요. 홍박사입니다. 정말 오랜만에 포스팅을 합니다. 바쁘다는 핑계로 계속 포스팅을 미뤄오다가 마음을 다잡고 짧은 호흡으로라도 포스팅을 하는 것이 좋을 것 같다는 생각이 들었습니
drhongdatanote.tistory.com
https://ko.wikipedia.org/wiki/%EC%A4%91%EC%8B%AC_%EA%B7%B9%ED%95%9C_%EC%A0%95%EB%A6%AC
중심 극한 정리 - 위키백과, 우리 모두의 백과사전
매우 불규칙한 분포도 충분히 많은 수를 더하면 중심극한정리에 따라 결국 정규분포로 수렴한다. 주사위를 n개 흔들 때 나오는 눈의 합 S n = X 1 + ... + X n의 분포가 n이 확대됨에 따라 정규 분포에
ko.wikipedia.org
'🖥 Computer Science > 확률과 통계' 카테고리의 다른 글
| [확률과 통계] - (16) Prior and Posterior Distributions (사전 분포와 사후 분포) (0) | 2022.05.16 |
|---|---|
| [확률과 통계] - (15) 추정(Estimation) (모수[Parameter] 추청) (0) | 2022.05.16 |
| [확률과 통계] - (13) 큰 수의 법칙(Law of Large Numbers) (0) | 2022.05.16 |
| [확률과 통계] - (12) Markov’s inequality(마르코브 부등식), Chebyshev's inequality(체비쇼프 부등식) (0) | 2022.05.16 |
| [확률과 통계] - (11) Sample Mean(표본평균) (0) | 2022.05.09 |