-
🧐 Spanning Tree
-
🧐 최소 신장 트리 (MST)
-
🧐 Kruskal's Algorithm
-
⭐️ 수도코드 - DFS 사용
-
🧐 증명
-
⭐️ Lemma 1 - feasibility(가용성)
-
⭐️ Lemma 2 - optimality(최적)
-
🧐 Union-Find를 사용한 Kruskal's Algorithm
-
⭐️ 수도코드 - Union Find 사용
-
🧐 Prim's Algorithm
-
-
-
⭐️ Cut Property
-
⭐️ 알고리즘
-
⭐️ 수도코드
-
🧐 Prim's Algorithm using Priority Queue
-
⭐️ 수도코드 ( 우선순위 큐 사용 )
🧐 Spanning Tree
그레프 내의 모든 정점을 포함하는 트리들 중, 최소 연결 트리를 의미합니다.
최소 연결의 의미는 간선의 수가 가장 적다는 것을 의미하며, 이를 위해서는 사이클이 존재해서는 안됩니다.
따라서 정점의 수가 $n$ 개인 그래프의 Spanning Tree는 edge가 정확히 $n-1$ 개 존재합니다.
또한 하나의 그래프에는 많은 신장 트리가 존재할 수 있습니다.
🧐 최소 신장 트리 (MST)
신장 트리들 중 edge들의 비용(cost)의 총 합이 최소인 트리를 의미합니다.
동일한 Cost를 가지는 Edge가 여러개 있을 경우 MST도 여러 종류가 나올 수 있으며,
반대로 모든 Edge들의 cost가 구분가능한 경우 MST는 단 하나만 존재할 수 있습니다.
(이는 뒤에서 증명해 보도록 하겠습니다 :D)
다음은 하나의 그래프에 대한 여러 MST를 나타낸 것입니다.
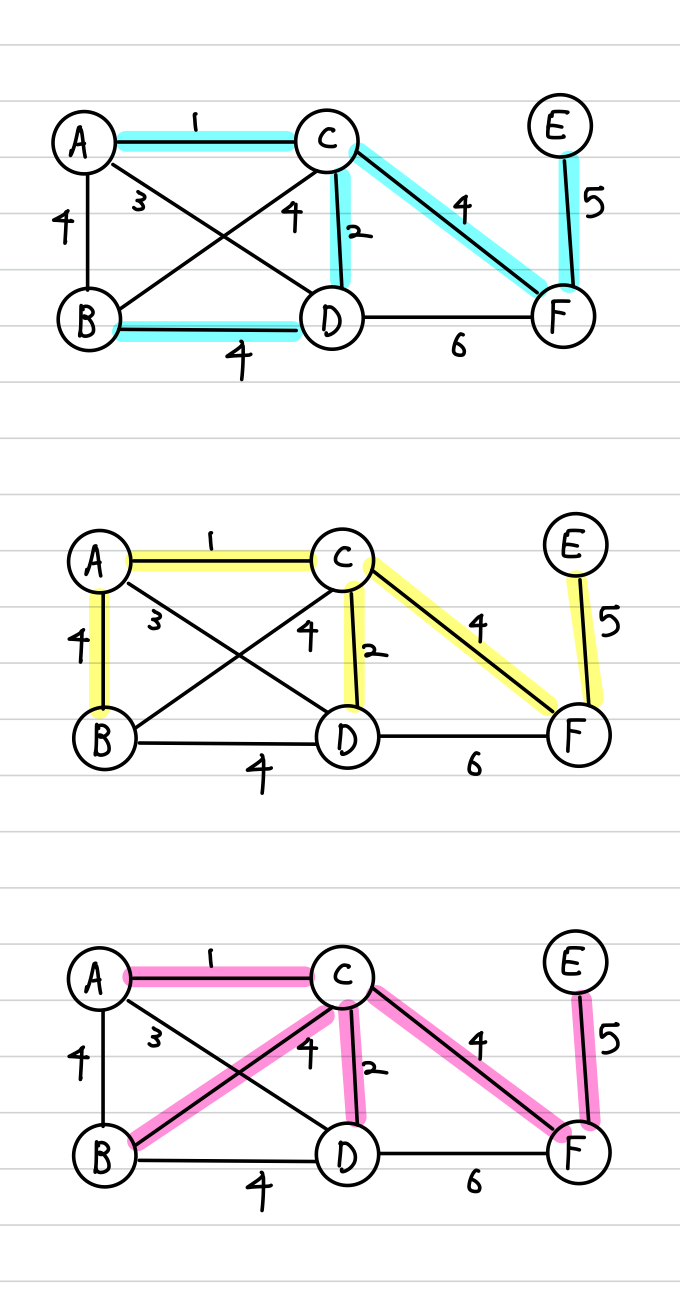
MST를 구하는 알고리즘으로는 크루스칼 알고리즘과 프림의 알고리즘이 있으며, 하나하나 살펴보도록 하겠습니다.
두 알고리즘 모두 Greedy Algorithm 에 속합니다.
(정말 정말 간단하게는)
크루스칼 알고리즘은 edge를 이용하여 MST를 구하며,
프림 알고리즘은 vertex를 이용하여 MST를 구합니다.
🧐 Kruskal's Algorithm
크루스칼 알고리즘은 다음과 같은 과정으로 MST를 구합니다.
우선 전제는 다음과 같습니다.
Connected graph $G$ 가 주어졌을 때, $G$ 의 MST를 $G'$ 으로 표시하며, $G'$ 의 Edge Set을 $T$ 로 나타냅니다.
1. $T$ 를 Empty Set으로 두고 시작합니다.
2. 현재 $T$ 에 추가하더라도 사이클이 생기지 않는 edge들 중, 가중치(cost)가 가장 작은 edge를 $T$ 에 추가합니다.
(이와 같이 $T$ 에 edge $e$ 를 추가해도 spanning tree의 조건을 만족할 때, $T + e$ 는 feasible(가용)하다고 합니다.)
(Spanning Tree의 조건: Connected + 최소 개수의 간선)
3. 2의 과정을 반복합니다.
⭐️ 수도코드 - DFS 사용
알고리즘의 수도코드는 다음과 같습니다.

(1) : 정렬에는 O( $m \; log \; n$ ) 시간이 소요됩니다.
(2) : 사이클 여부 판단은 $G' = (V(G), T)$ 에 대하여 DFS를 수행하여 판단합니다.
따라서 각 edge를 추가할 때마다 최대 $O(n + m)$의 시간이 걸리므로 $O(m (n + m))$
(e를 추가하여 explore를 하며 backedge가 있다면 사이클)
따라서 위의 알고리즘은 총 $O(m log n) + O(m(n+m)) = O(m^{2})$ 시간이 소요됩니다.
이를 더 빠르게 개선하기 위해 Union-Find 자료구조를 사용할 수 있습니다.
그러나 그 전에, 크루스칼 알고리즘이 최적해를 반환함을 증명해보도록 하겠습니다.
🧐 증명
저희가 증명하고자 하는 것은 크루스칼 알고리즘은 항상 최적해를 반환한다는 것입니다.
이를 증명하기 위해 다음과 같은 보조정리들을 증명해보도록 하겠습니다.
⭐️ Lemma 1 - feasibility(가용성)
증명하고자 하는 주장은 다음과 같습니다.
크루스칼 알고리즘의 결과물 $G' = (V(G), T)$ 는 항상 connected 하다.
증명은 귀류법을 통해 진행되며 아래와 같습니다.
$G'$ 이 connected 가 아니라 가정하겠습니다.
$V_1, V_2, ..., V_r$ 을 $G'$ 의 connected component들이라 하겠습니다.
$G$ 는 connected 하므로, 일반성을 잃지 않고
$V_1$ 상의 정점과 $V(G) \setminus V_1 $ 상의 정점을 이어주는 edge $e$가 언제나 적어도 하나 존재합니다.
해당 edge $e$ 를 $G'$ 에 추가하더라도 그래프는 여전이 acyclic 합니다.
따라서 크루스칼 알고리즘은 edge $e$ 를 추가한다는 것에 모순이 발생하며, $G'$ 는 항상 connected 하다고 볼 수 있습니다.
⭐️ Lemma 2 - optimality(최적)
증명하고자 하는 주장은 다음과 같습니다.
크루스칼 알고리즘은 $G$ 의 edge들의 cost가 모두 다를 때, 유일한 MST를 반환한다.
(같은 cost를 가진 edge가 있는 경우, MST는 만들어지지만 유일함은 성립하지 않습니다.)
증명은 귀류법으로 이루어지며 다음과 같습니다.
$T$ 를 크루스칼 알고리즘이 포함하는 edge set,
$T'$ 을 optimal solution(MST)가 포함하는 edge set 이라 하겠습니다.
만약 $T \neq T'$ 라면, $T' \setminus T$ (최적해에 포함되지 않는 간선 중 크루스칼 알고리즘이 고른 간선)에 속하는 간선 $e = (u, v)$ 가 존재해야 합니다.
이때 크루스칼 알고리즘에 의해 $T$ 에서 $u$ 에서 $v$ 까지의 path를 이루는 edge들의 cost의 총 합은 $e$ 의 cost보다 작습니다. (아닌 경우 크루스칼 알고리즘은 e를 반드시 포함합니다.)
이때 $e' $ 를 $T$ 에서 $u$ 에서 $v$ 까지의 path 중 임의의 edge라고 하면,
$T' \setminus \left\{ e \right\} \cup \left\{ e' \right\}$ 의 총 cost는 $T'$ 의 총 cost보다 작으며, 해당 edge들은 여전히 spanning tree를 이룹니다.
따라서 $T'$ 이 optimal 이라는 가정에 모순됩니다.
따라서 주장이 증명됩니다.
🧐 Union-Find를 사용한 Kruskal's Algorithm
Union-Find 자료구조를 사용하면
인접한 두 정점 $v, u$ 에 대하여 find()의 결과가 같은 경우 해당 edge를 추가하게 된다면 사이클이 생기는 것이라 판단할 수 있습니다.
즉 Cycle이 생기는 조건은 다음과 같습니다.
$find(u) == find(v)$
해당 성질을 이용하여 크루스칼 알고리즘을 구현하는 수도코드를 살펴보도록 하겠습니다.
⭐️ 수도코드 - Union Find 사용

(1) : n개의 정점에 대해 수행하므로 $O(n)$
(2) : 정렬하는데 걸리는 시간은 $O(m \; log \; n )$
(3) : find 밑 union 연산을 최대 m 번(간선의 개수) 진행하므로 $O(m \; log\; n)$
따라서 총 $O(m \; log\; n)$ 의 시간이 소요됩니다.
(3) 의 경우 union-find 게시글에서 알아본 property 3에 의하여 성립합니다.
$|V(G)| = n$ 이라고 할때,
m의 최대 개수는 $G$ 의 vertex들 중 중복없이 무작위로 2개 고른 수와 같고, 이는 $\theta(n^2)$ 입니다.
find 및 union은 edge 개수인 m개에 대해 m번 발생하는데,
한번 발생할 때마다 $log \; m = log(n^2)$ 이고, $log(n^2) = 2\;log\;n $ 입니다.
🧐 Prim's Algorithm
MST를 구하는 또 다른 알고리즘입니다.
Cut Property 를 사용합니다.
⭐️ Cut Property
간선 e = ($u$, $v$) 는 MST의 간선들의 집합 $T$ 에 속해 있다
if and only if
e 는 정점 $u$를 포함한 어떤 정점들의 집합 $S$와,
$v$ 를 포함한 $V(G) \setminus S$ 를 이어주는 간선들 중 제일 cost가 작다
증명은 다음과 같습니다.
1. MST 가 위에 해당하는 e 대신, $S$ 와 $V(G) - S$ 를 이어주는 다른 edge $e'$ 를 가지고 있다고 가정하겠습니다.
그러면 e의 성질에 의하여 $T - \left\{ e'\right\} \cup \left\{ e\right\}$ 의 총 cost는 기존의 $T$ 의 총 cost보다 작아지므로, $T$가 MST의 간선들에 집합에 속한다는 가정에 모순입니다.
2. $T$ 가 어떤 MST를 이루는 간선들의 집합이라 하고,
$S$ 와 $V(G) - S$ 를 각각 $T - \left\{ e \right\}$ 의 connected component에 속하는 정점들의 집합이라 하겠습니다.
이때 $e = (u,v)$ 에서 $u$ 와 $v$ 를 이어주는 $e$ 가 아닌 edge $e' $ 에 대하여,
$e'$ 의 cost가 $e$ 보다 더 작다고 가정하겠습니다.
그러면 $T - \left\{ e'\right\} \cup \left\{ e\right\}$ 의 총 cost는 기존의 $T$ 의 총 cost보다 작아지므로,
T가 MST의 edge set 이라는 가정에 모순입니다.
Cut Property에 의해 어떤 임의의 정점들의 집합$S$ (S는 $V(G)$ 의 진부분집합) 에 대하여,
MST는 $S$와 $V(G) \setminus S$ 를 이어주는 간선들 중 cost가 가장 작은 간선을 언제나 포함한다는 것을 알 수 있습니다.
따라서 $S$ 에 속한 정점을 하나씩 늘려가며 cut property를 만족시키도록 간선을 고르면 MST를 생성할 수 있습니다.
⭐️ 알고리즘
다음과 같은 과정으로 이루어집니다.
1. $S = \left\{ v \right\}$ 로 설정합니다.
$v$ 는 $G$ 상의 아무 vertex나 상관없습니다.
2. $S$ 와 $V(G) \setminus S$ 를 이어주는 edge들 중 가장 작은 cost를 가진 $e = (v, w)$를, MST의 edge set $T$ 에 추가합니다.
3. vertex $w$ 를 $S$ 에 추가합니다.
4. 2번과 3번의 과정을 $S = V(G)$ 가 될 때까지 반복합니다.
⭐️ 수도코드

(1) : 정점의 개수인 n번 반복하므로 $O(n)$
(2) : 해당 조건에 해당하는 edge를 찾기 위해 $v, w$ 를 연결하는 edge를 모두 검사해야 하므로 최대 $O(m)$
따라서 총 $O(nm)$ 의 시간 복잡도를 가집니다.
속도를 더 높이기 위해서는 Priority Queue를 사용할 수 있습니다.
🧐 Prim's Algorithm using Priority Queue
사용되는 Priority Queue의 연산은 다음과 같습니다.
(이때 Priority Queue는 수가 낮을수록 우선순위가 높다고 설정되었다고 가정합니다.)
1. findmin() : Priority Queue 에서 priority가 가장 높은 item 반환
2. deletemin() : Priority Queue 에서 priority가 가장 높은 item을 제거 후 반환
3. insert(item) : Priority Queue 에 새로운 item 추가
4. delete(item) : item을 Priority Queue 에서 제거하고 반환
5. decreasekey(item, k) : item의 priority를 k로 변경
1번은 $O(1)$
2, 3번은 $O(log \; n)$
4번은 heap의 위치를 저장하는 array를 만들어 deletemin과 비슷하게 해당 heap의 node를 제거할 수 있으므로 $O(log \; n)$
5번은 delete + insert를 통해 우선순위를 변경할 수 있으므로, $O(log\;n)$
이를 사용한 알고리즘은 다음과 같습니다.
우선 $cost(v)$ 를 다음과 같이 정의합니다.
$V(G)$ 에 속한 정점 $v$ 에 대하여 $cost(v) = min_{u \in S} e(u, v)$
즉 $v$ 에 인접한 정점들 중 비용이 최소인 간선의 cost가 cost(v)가 됩니다.
1. $cost(v)$ 의 초기값은 Prim 알고리즘을 시작할 첫번째 정점을 제외하고는 모두 무한대로 설정합니다.
첫번째 정점은 0으로 설정합니다.
또한 $G$의 각 정점 a 에 대하여, pre(a) 라고 하는 포인터를 두고 초기값을 null(아무것도 가리키지 않음)로 둡니다.
2. 정점들의 비용이 작을수록 우선순위가 높도록 설정된 우선순위 큐 H 에 대하여, 모든 정점들을 삽입합니다.
3. H 에서 deletemin 을 통해 얻은 정점 v 를 $S$ 에 추가합니다.
이후 pre(v) 가 null이 아닌 경우 간선 (v, pre(v)) 를 MST의 간선들의 집합 $T$ 에 추가합니다.
(deletemin을 통해 얻은 정점 v 는 MST에 속하는 정점들의 집합 $S$ 와,
$V(G) - S$ 를 이어주는 정점들 중 가장 비용이 낮은 간선에 포함되며,
v 는 아직 MST에 속하지 않았기 때문에 이를 추가해 주는 것입니다.)
4. 3번에서 꺼낸 v 에 대해, v 와 인접한 모든 정점들의 비용을 다시 계산하여,
cost 값을 변경해야 하는 경우 decreasekey를 사용하여 변경합니다.
이때 v 와 인접한 어느 정점 z 에 대하여 edge e = (v, z) 로 인해 cost(z) 의 값이 변경되었다면,
pre(z) = v 로 변경합니다.
5. 3번과 4번의 과정을 우선순위 큐 $H$ 가 완전히 빌 때까지 반복합니다.
⭐️ 수도코드 ( 우선순위 큐 사용 )

(1) : makequeue는 n번의 insert가 필요하므로 $O(n \; log\; n)$
(2) : deletemin 역시 n의 개수만큼 실행되므로 $O(n \; log\; n)$
(3) : 각 edge를 최대 2번 확인하며, decreasekey는 최대 m번 수행되기 때문에 $O(m \; log\; n)$
따라서 총 $O((m+n) \;log\; n)$ 시간이 소요됩니다.
(3)번의 경우 decresekey는 cost가 업데이트 될때만 수행하는데,
초기화 시 edge가 전부 무한대로 설정하므로 해당 edge를 처음 만날때에 cost가 업데이트됩니다.
그 이후 다시 해당 edge를 만나면 이미 업데이트된 cost라서 decreasekey를 하지 않으므로
decreasekey는 최대 m번(간선의 개수) 수행되는 것입니다.
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그리디 (3) - Huffman Encoding(허프만 부호화) (0) | 2022.10.21 |
|---|---|
| [알고리즘] 그리디 (2) - Interval scheduling (0) | 2022.10.21 |
| [알고리즘] 그리디 (0) -그리디 알고리즘 (0) | 2022.10.13 |
| [알고리즘] 유니온 파인드(Union-Find) 자료구조 (0) | 2022.10.03 |
| [알고리즘] 그래프 (7) - 강한 연결 요소 (Strongly Connected Components) (1) | 2022.09.25 |
🧐 Spanning Tree
그레프 내의 모든 정점을 포함하는 트리들 중, 최소 연결 트리를 의미합니다.
최소 연결의 의미는 간선의 수가 가장 적다는 것을 의미하며, 이를 위해서는 사이클이 존재해서는 안됩니다.
따라서 정점의 수가 $n$ 개인 그래프의 Spanning Tree는 edge가 정확히 $n-1$ 개 존재합니다.
또한 하나의 그래프에는 많은 신장 트리가 존재할 수 있습니다.
🧐 최소 신장 트리 (MST)
신장 트리들 중 edge들의 비용(cost)의 총 합이 최소인 트리를 의미합니다.
동일한 Cost를 가지는 Edge가 여러개 있을 경우 MST도 여러 종류가 나올 수 있으며,
반대로 모든 Edge들의 cost가 구분가능한 경우 MST는 단 하나만 존재할 수 있습니다.
(이는 뒤에서 증명해 보도록 하겠습니다 :D)
다음은 하나의 그래프에 대한 여러 MST를 나타낸 것입니다.

MST를 구하는 알고리즘으로는 크루스칼 알고리즘과 프림의 알고리즘이 있으며, 하나하나 살펴보도록 하겠습니다.
두 알고리즘 모두 Greedy Algorithm 에 속합니다.
(정말 정말 간단하게는)
크루스칼 알고리즘은 edge를 이용하여 MST를 구하며,
프림 알고리즘은 vertex를 이용하여 MST를 구합니다.
🧐 Kruskal's Algorithm
크루스칼 알고리즘은 다음과 같은 과정으로 MST를 구합니다.
우선 전제는 다음과 같습니다.
Connected graph $G$ 가 주어졌을 때, $G$ 의 MST를 $G'$ 으로 표시하며, $G'$ 의 Edge Set을 $T$ 로 나타냅니다.
1. $T$ 를 Empty Set으로 두고 시작합니다.
2. 현재 $T$ 에 추가하더라도 사이클이 생기지 않는 edge들 중, 가중치(cost)가 가장 작은 edge를 $T$ 에 추가합니다.
(이와 같이 $T$ 에 edge $e$ 를 추가해도 spanning tree의 조건을 만족할 때, $T + e$ 는 feasible(가용)하다고 합니다.)
(Spanning Tree의 조건: Connected + 최소 개수의 간선)
3. 2의 과정을 반복합니다.
⭐️ 수도코드 - DFS 사용
알고리즘의 수도코드는 다음과 같습니다.

(1) : 정렬에는 O( $m \; log \; n$ ) 시간이 소요됩니다.
(2) : 사이클 여부 판단은 $G' = (V(G), T)$ 에 대하여 DFS를 수행하여 판단합니다.
따라서 각 edge를 추가할 때마다 최대 $O(n + m)$의 시간이 걸리므로 $O(m (n + m))$
(e를 추가하여 explore를 하며 backedge가 있다면 사이클)
따라서 위의 알고리즘은 총 $O(m log n) + O(m(n+m)) = O(m^{2})$ 시간이 소요됩니다.
이를 더 빠르게 개선하기 위해 Union-Find 자료구조를 사용할 수 있습니다.
그러나 그 전에, 크루스칼 알고리즘이 최적해를 반환함을 증명해보도록 하겠습니다.
🧐 증명
저희가 증명하고자 하는 것은 크루스칼 알고리즘은 항상 최적해를 반환한다는 것입니다.
이를 증명하기 위해 다음과 같은 보조정리들을 증명해보도록 하겠습니다.
⭐️ Lemma 1 - feasibility(가용성)
증명하고자 하는 주장은 다음과 같습니다.
크루스칼 알고리즘의 결과물 $G' = (V(G), T)$ 는 항상 connected 하다.
증명은 귀류법을 통해 진행되며 아래와 같습니다.
$G'$ 이 connected 가 아니라 가정하겠습니다.
$V_1, V_2, ..., V_r$ 을 $G'$ 의 connected component들이라 하겠습니다.
$G$ 는 connected 하므로, 일반성을 잃지 않고
$V_1$ 상의 정점과 $V(G) \setminus V_1 $ 상의 정점을 이어주는 edge $e$가 언제나 적어도 하나 존재합니다.
해당 edge $e$ 를 $G'$ 에 추가하더라도 그래프는 여전이 acyclic 합니다.
따라서 크루스칼 알고리즘은 edge $e$ 를 추가한다는 것에 모순이 발생하며, $G'$ 는 항상 connected 하다고 볼 수 있습니다.
⭐️ Lemma 2 - optimality(최적)
증명하고자 하는 주장은 다음과 같습니다.
크루스칼 알고리즘은 $G$ 의 edge들의 cost가 모두 다를 때, 유일한 MST를 반환한다.
(같은 cost를 가진 edge가 있는 경우, MST는 만들어지지만 유일함은 성립하지 않습니다.)
증명은 귀류법으로 이루어지며 다음과 같습니다.
$T$ 를 크루스칼 알고리즘이 포함하는 edge set,
$T'$ 을 optimal solution(MST)가 포함하는 edge set 이라 하겠습니다.
만약 $T \neq T'$ 라면, $T' \setminus T$ (최적해에 포함되지 않는 간선 중 크루스칼 알고리즘이 고른 간선)에 속하는 간선 $e = (u, v)$ 가 존재해야 합니다.
이때 크루스칼 알고리즘에 의해 $T$ 에서 $u$ 에서 $v$ 까지의 path를 이루는 edge들의 cost의 총 합은 $e$ 의 cost보다 작습니다. (아닌 경우 크루스칼 알고리즘은 e를 반드시 포함합니다.)
이때 $e' $ 를 $T$ 에서 $u$ 에서 $v$ 까지의 path 중 임의의 edge라고 하면,
$T' \setminus \left\{ e \right\} \cup \left\{ e' \right\}$ 의 총 cost는 $T'$ 의 총 cost보다 작으며, 해당 edge들은 여전히 spanning tree를 이룹니다.
따라서 $T'$ 이 optimal 이라는 가정에 모순됩니다.
따라서 주장이 증명됩니다.
🧐 Union-Find를 사용한 Kruskal's Algorithm
Union-Find 자료구조를 사용하면
인접한 두 정점 $v, u$ 에 대하여 find()의 결과가 같은 경우 해당 edge를 추가하게 된다면 사이클이 생기는 것이라 판단할 수 있습니다.
즉 Cycle이 생기는 조건은 다음과 같습니다.
$find(u) == find(v)$
해당 성질을 이용하여 크루스칼 알고리즘을 구현하는 수도코드를 살펴보도록 하겠습니다.
⭐️ 수도코드 - Union Find 사용

(1) : n개의 정점에 대해 수행하므로 $O(n)$
(2) : 정렬하는데 걸리는 시간은 $O(m \; log \; n )$
(3) : find 밑 union 연산을 최대 m 번(간선의 개수) 진행하므로 $O(m \; log\; n)$
따라서 총 $O(m \; log\; n)$ 의 시간이 소요됩니다.
(3) 의 경우 union-find 게시글에서 알아본 property 3에 의하여 성립합니다.
$|V(G)| = n$ 이라고 할때,
m의 최대 개수는 $G$ 의 vertex들 중 중복없이 무작위로 2개 고른 수와 같고, 이는 $\theta(n^2)$ 입니다.
find 및 union은 edge 개수인 m개에 대해 m번 발생하는데,
한번 발생할 때마다 $log \; m = log(n^2)$ 이고, $log(n^2) = 2\;log\;n $ 입니다.
🧐 Prim's Algorithm
MST를 구하는 또 다른 알고리즘입니다.
Cut Property 를 사용합니다.
⭐️ Cut Property
간선 e = ($u$, $v$) 는 MST의 간선들의 집합 $T$ 에 속해 있다
if and only if
e 는 정점 $u$를 포함한 어떤 정점들의 집합 $S$와,
$v$ 를 포함한 $V(G) \setminus S$ 를 이어주는 간선들 중 제일 cost가 작다
증명은 다음과 같습니다.
1. MST 가 위에 해당하는 e 대신, $S$ 와 $V(G) - S$ 를 이어주는 다른 edge $e'$ 를 가지고 있다고 가정하겠습니다.
그러면 e의 성질에 의하여 $T - \left\{ e'\right\} \cup \left\{ e\right\}$ 의 총 cost는 기존의 $T$ 의 총 cost보다 작아지므로, $T$가 MST의 간선들에 집합에 속한다는 가정에 모순입니다.
2. $T$ 가 어떤 MST를 이루는 간선들의 집합이라 하고,
$S$ 와 $V(G) - S$ 를 각각 $T - \left\{ e \right\}$ 의 connected component에 속하는 정점들의 집합이라 하겠습니다.
이때 $e = (u,v)$ 에서 $u$ 와 $v$ 를 이어주는 $e$ 가 아닌 edge $e' $ 에 대하여,
$e'$ 의 cost가 $e$ 보다 더 작다고 가정하겠습니다.
그러면 $T - \left\{ e'\right\} \cup \left\{ e\right\}$ 의 총 cost는 기존의 $T$ 의 총 cost보다 작아지므로,
T가 MST의 edge set 이라는 가정에 모순입니다.
Cut Property에 의해 어떤 임의의 정점들의 집합$S$ (S는 $V(G)$ 의 진부분집합) 에 대하여,
MST는 $S$와 $V(G) \setminus S$ 를 이어주는 간선들 중 cost가 가장 작은 간선을 언제나 포함한다는 것을 알 수 있습니다.
따라서 $S$ 에 속한 정점을 하나씩 늘려가며 cut property를 만족시키도록 간선을 고르면 MST를 생성할 수 있습니다.
⭐️ 알고리즘
다음과 같은 과정으로 이루어집니다.
1. $S = \left\{ v \right\}$ 로 설정합니다.
$v$ 는 $G$ 상의 아무 vertex나 상관없습니다.
2. $S$ 와 $V(G) \setminus S$ 를 이어주는 edge들 중 가장 작은 cost를 가진 $e = (v, w)$를, MST의 edge set $T$ 에 추가합니다.
3. vertex $w$ 를 $S$ 에 추가합니다.
4. 2번과 3번의 과정을 $S = V(G)$ 가 될 때까지 반복합니다.
⭐️ 수도코드

(1) : 정점의 개수인 n번 반복하므로 $O(n)$
(2) : 해당 조건에 해당하는 edge를 찾기 위해 $v, w$ 를 연결하는 edge를 모두 검사해야 하므로 최대 $O(m)$
따라서 총 $O(nm)$ 의 시간 복잡도를 가집니다.
속도를 더 높이기 위해서는 Priority Queue를 사용할 수 있습니다.
🧐 Prim's Algorithm using Priority Queue
사용되는 Priority Queue의 연산은 다음과 같습니다.
(이때 Priority Queue는 수가 낮을수록 우선순위가 높다고 설정되었다고 가정합니다.)
1. findmin() : Priority Queue 에서 priority가 가장 높은 item 반환
2. deletemin() : Priority Queue 에서 priority가 가장 높은 item을 제거 후 반환
3. insert(item) : Priority Queue 에 새로운 item 추가
4. delete(item) : item을 Priority Queue 에서 제거하고 반환
5. decreasekey(item, k) : item의 priority를 k로 변경
1번은 $O(1)$
2, 3번은 $O(log \; n)$
4번은 heap의 위치를 저장하는 array를 만들어 deletemin과 비슷하게 해당 heap의 node를 제거할 수 있으므로 $O(log \; n)$
5번은 delete + insert를 통해 우선순위를 변경할 수 있으므로, $O(log\;n)$
이를 사용한 알고리즘은 다음과 같습니다.
우선 $cost(v)$ 를 다음과 같이 정의합니다.
$V(G)$ 에 속한 정점 $v$ 에 대하여 $cost(v) = min_{u \in S} e(u, v)$
즉 $v$ 에 인접한 정점들 중 비용이 최소인 간선의 cost가 cost(v)가 됩니다.
1. $cost(v)$ 의 초기값은 Prim 알고리즘을 시작할 첫번째 정점을 제외하고는 모두 무한대로 설정합니다.
첫번째 정점은 0으로 설정합니다.
또한 $G$의 각 정점 a 에 대하여, pre(a) 라고 하는 포인터를 두고 초기값을 null(아무것도 가리키지 않음)로 둡니다.
2. 정점들의 비용이 작을수록 우선순위가 높도록 설정된 우선순위 큐 H 에 대하여, 모든 정점들을 삽입합니다.
3. H 에서 deletemin 을 통해 얻은 정점 v 를 $S$ 에 추가합니다.
이후 pre(v) 가 null이 아닌 경우 간선 (v, pre(v)) 를 MST의 간선들의 집합 $T$ 에 추가합니다.
(deletemin을 통해 얻은 정점 v 는 MST에 속하는 정점들의 집합 $S$ 와,
$V(G) - S$ 를 이어주는 정점들 중 가장 비용이 낮은 간선에 포함되며,
v 는 아직 MST에 속하지 않았기 때문에 이를 추가해 주는 것입니다.)
4. 3번에서 꺼낸 v 에 대해, v 와 인접한 모든 정점들의 비용을 다시 계산하여,
cost 값을 변경해야 하는 경우 decreasekey를 사용하여 변경합니다.
이때 v 와 인접한 어느 정점 z 에 대하여 edge e = (v, z) 로 인해 cost(z) 의 값이 변경되었다면,
pre(z) = v 로 변경합니다.
5. 3번과 4번의 과정을 우선순위 큐 $H$ 가 완전히 빌 때까지 반복합니다.
⭐️ 수도코드 ( 우선순위 큐 사용 )

(1) : makequeue는 n번의 insert가 필요하므로 $O(n \; log\; n)$
(2) : deletemin 역시 n의 개수만큼 실행되므로 $O(n \; log\; n)$
(3) : 각 edge를 최대 2번 확인하며, decreasekey는 최대 m번 수행되기 때문에 $O(m \; log\; n)$
따라서 총 $O((m+n) \;log\; n)$ 시간이 소요됩니다.
(3)번의 경우 decresekey는 cost가 업데이트 될때만 수행하는데,
초기화 시 edge가 전부 무한대로 설정하므로 해당 edge를 처음 만날때에 cost가 업데이트됩니다.
그 이후 다시 해당 edge를 만나면 이미 업데이트된 cost라서 decreasekey를 하지 않으므로
decreasekey는 최대 m번(간선의 개수) 수행되는 것입니다.
'🖥 Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그리디 (3) - Huffman Encoding(허프만 부호화) (0) | 2022.10.21 |
|---|---|
| [알고리즘] 그리디 (2) - Interval scheduling (0) | 2022.10.21 |
| [알고리즘] 그리디 (0) -그리디 알고리즘 (0) | 2022.10.13 |
| [알고리즘] 유니온 파인드(Union-Find) 자료구조 (0) | 2022.10.03 |
| [알고리즘] 그래프 (7) - 강한 연결 요소 (Strongly Connected Components) (1) | 2022.09.25 |
