이진 검색 트리란?
BinarySearchTree 인터페이스
public interface BinarySearchTree<Key extends Comparable<Key> >{
boolean isEmpty();
boolean isFull();
int size();
boolean contains(Key key);
Key get(Key key);
boolean add(Key key);
Key remove(Key key);
void inOrder();
void clear();
}
BinaryNode<E> 구현
BST의 내부 노드로 사용할 BinaryNode는 다음과 같습니다.
public class BinaryNode<E> {
private E element;
private BinaryNode<E> left;
private BinaryNode<E> right;
public boolean hasLeft(){
return this.left != null;
}
public boolean hasRight(){
return this.right != null;
}
public boolean isLeaf() {
return this.left == null && this.right == null;
}
public boolean hasOneChild() {
return !isLeaf() && !hasTwoChild();
}
public boolean hasTwoChild() {
return this.left != null && this.right != null;
}
public BinaryNode(E element) {this.element = element;}
public E element() {return this.element;}
public void setElement(E element) {this.element = element;}
public BinaryNode<E> left() {return left;}
public void setLeft(BinaryNode<E> left) {this.left = left;}
public BinaryNode<E> right() {return right;}
public void setRight(BinaryNode<E> right) {this.right = right;}
}
세부 구현
우선 필드와 기본적인 메서드부터 확인하겠습니다.
public class BSTByLinkedNode <Key extends Comparable<Key>> implements BinarySearchTree<Key>{
private BinaryNode<Key> root;
private int size;
//== Getter / Setter ==//
public BinaryNode<Key> root() {
return root;
}
private void setRoot(BinaryNode<Key> root) {
this.root = root;
}
private void setSize(int size) {
this.size = size;
}
@Override
public boolean isEmpty() {
return this.size == 0;
}
@Override
public boolean isFull() {
return false;
}
BST에서 중요한 부분은 조회, 삽입, 삭제의 구현입니다.
우선 가장 간단한 조회부터 확인하겠습니다.
조회
public Key get(Key key) {
BinaryNode<Key> current = this.root;
while (current != null) {
int compareTo = key.compareTo(current.element());
//== Key 가 더 큰 경우 ==//
if (compareTo > 0) {current = current.right();}
//== Key 가 더 작은 경우 ==//
if (compareTo < 0) {current = current.left();}
//== 동일한 경우 ==//
if (compareTo == 0) {return current.element();}
}
return null;
}설명
우선 root 노드를 current로 설정합니다.
이후 current가 null이 될 때까지 아래 과정을 반복합니다.
- current의 key와 입력받은 키를 비교합니다.
- 입력받은 키가 더 큰 경우, 찾는 값은 우측 서브트리에 존재하므로 current를 current.right()로 바꾸어줍니다.
- 입력받은 키가 더 작은 경우, 찾는 값은 좌측 서브트리에 존재하므로 current를 current.left()로 바꾸어줍니다.
- 키가 동일한 것이므로 해당 값을 반환합니다.
삽입
@Override
public boolean add(Key key) {
BinaryNode<Key> addNode = new BinaryNode<>(key);
if(isEmpty()) {
setRoot(addNode);
this.size ++;
return true;
}
BinaryNode<Key> current = this.root;
while (current != null) {
int compareTo = key.compareTo(current.element());
//== Key 가 더 큰 경우 ==//
if (compareTo > 0) {
if (current.hasRight()) {current = current.right();}
else {
current.setRight(addNode);
break;
}
}
//== Key 가 더 작은 경우 ==//
if (compareTo < 0) {
if (current.hasLeft()) {current = current.left();}
else {
current.setLeft(addNode);
break;
}
}
//== 동일한 경우 -> 이미 존재하므로 삽입 실패 ==//
if (compareTo == 0) {
return false;
}
}
this.size++;
return true;
}설명
루트가 비어있는 경우와 그렇지 않은 경우, 두 가지 상황을 구분하여 구현합니다.
우선 공통적으로 추가할 key를 가진 BinaryNode를 하나 생성합니다. 이름은 addNode라 짓겠습니다.
1. 루트가 비어있는 경우
root에 addNode를 저장한 후, size를 1 증가시킨 뒤 true를 반환합니다.
2. 루트가 비어있지 않은 경우
조회와 마찬가지로 탐색을 진행해야 합니다.
우선 root를 current로 설정한 후, 조회에서 했던 방식으로 current를 갱신합니다.
이때 다른 점이 있습니다.
2-1. 동일한 key가 발견되는 경우
이미 존재하는 key이기 때문에 false를 반환하며 종료합니다.
2-2. Current가 갱신되어야 할 때, 값이 없는 경우
Key가 current보다 작아 current를 current.left()로 갱신해야 하는 상황을 가정해봅시다.
그런데 만약 current의 left가 존재하지 않는다면, current의 left 위치에 해당 key 값을 가진 노드가 삽입되면 됩니다.
따라서 current의 left(key가 더 작은 경우) 혹은 right(Key가 더 큰 경우)가 없는 경우 해당 위치에 addNode를 삽입하는 코드를 작성하였습니다.
삭제 1
가장 어려운 부분입니다.
총 4가지 메서드가 존재하며 차례대로 살펴보겠습니다.
@Override
public Key remove(Key key) {
if (isEmpty()) return null;
int compareTo = key.compareTo(this.root.element());
if (compareTo == 0){
//== REMOVE ROOT !! ==//
return removeFromRoot();
}
return (compareTo > 0 )
? removeFromRight(key, this.root) //== Key 가 더 큰 경우 ==//
: removeFromLeft(key, this.root); //== Key 가 더 작은 경우 ==//
}
설명
다음과 같은 3가지 상황으로 구분합니다.
1. 루트가 없는 경우
2. 루트를 제거하는 경우
3. 루트의 서브트리에서 제거하는 경우
이때 루트가 없는 경우는 바로 null을 반환하므로 설명하지 않고 넘어가겠습니다.
루트를 제거하는 경우는 removeFromRoot 메서드에서 설명하고, 그렇지 않는 경우를 살펴보겠습니다.
Key가 루트보다 큰 경우, 제거할 Node는 루트의 우측 서브트리에 존재합니다.
따라서 우측 서브트리에서 값을 제거하는 removeFromRight를 실행합니다.
그렇지 않은 경우 (Key가 루트보다 작은 경우) 제거할 Node는 루트의 좌측 서브트리에 존재합니다.
따라서 좌측 서브트리에서 값을 제거하는 removeFromLeft를 실행합니다.
삭제 2 - removeFromRoot
private Key removeFromRoot() {
Key remove = this.root.element();
if (root.isLeaf()) {
setRoot(null);
}//루트가 Leaf 인 경우 바로 제거
else if (root.hasOneChild()){//루트의 자식이 하나만 있는 경우
if (root.hasLeft()) {setRoot(this.root.left());} //Left 가 존재한다면 Root를 Root의 Left로 수정
else {setRoot(this.root.right());}//Right 가 존재한다면 Root를 Root의 Right로 수정
}
//== 모두 존재하는 경우, left SubTree 에서 최댓값 제거한 후, 제거한 값을 요소로 세팅==//
else if (root.hasTwoChild()) {root.setElement(this.removeRightMostElementOfLeftTree(root));}
this.size --;
return remove;
}설명
루트가 Leaf 노드인 경우와, 자식이 하나인 경우, 자식이 두개인 경우를 각각 그림으로 설명하겠습니다.
1. Root가 Leaf
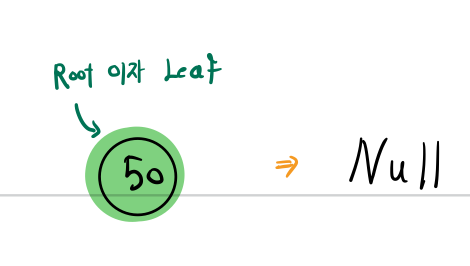
2. Root의 자식이 단 1개
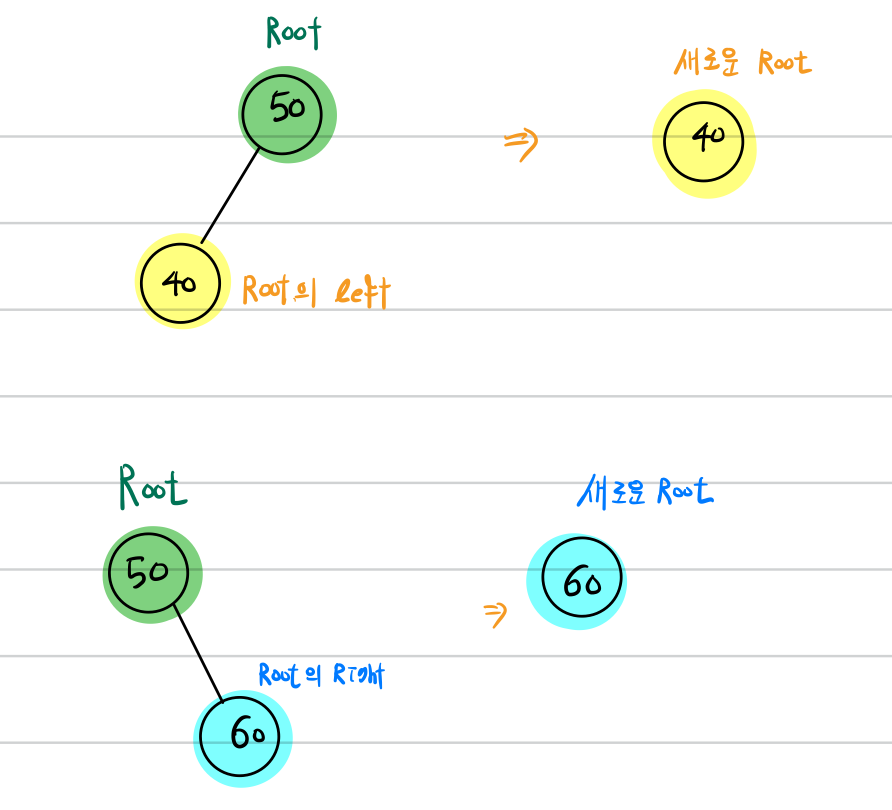
3. Root의 자식이 2개
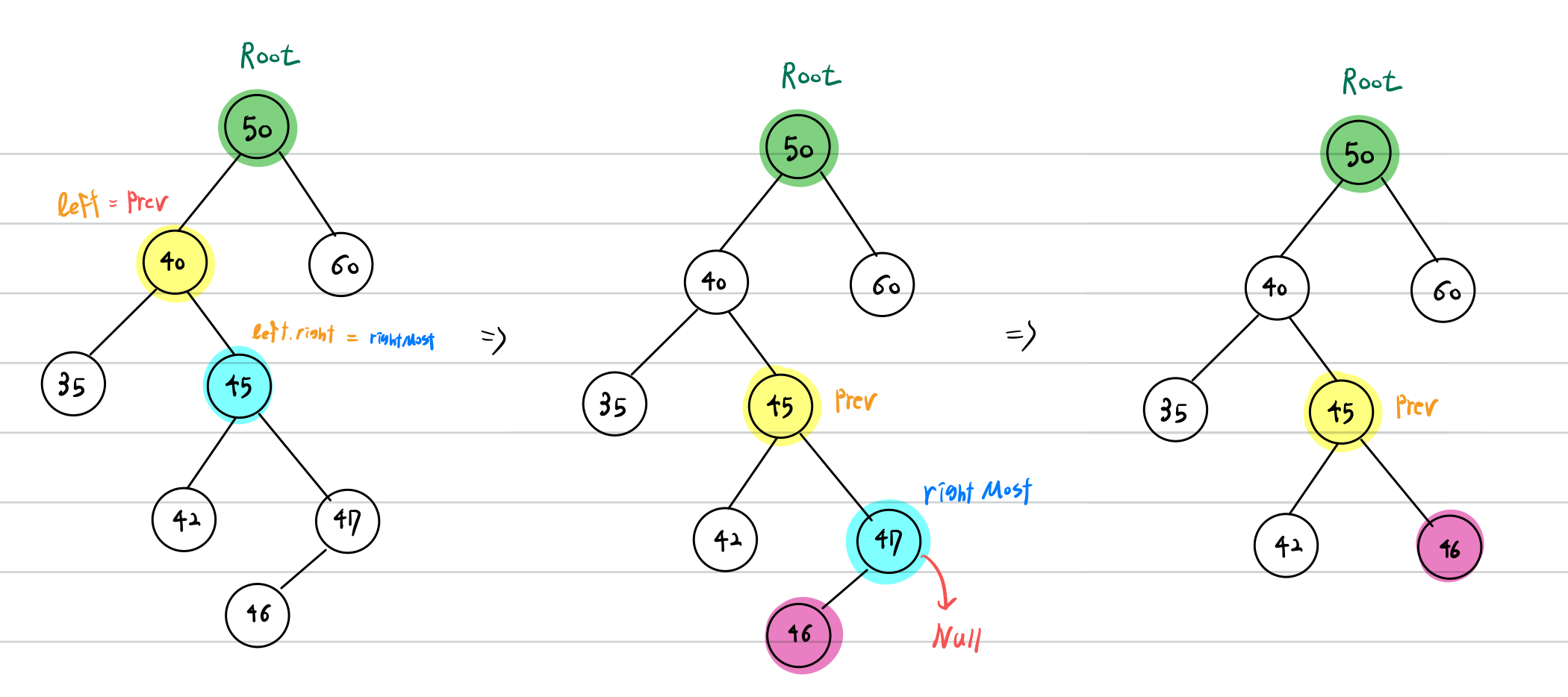
root의 element를 rightMost로 대체한 후, rightMost 삭제로 문제를 변형합니다.
즉 root의 삭제 문제가, rightMost의 삭제 문제로 바뀌었습니다.
이때 rightMost는 두가지 상황이 있을 수 있습니다.
rightMost의 left가 존재하거나, rightMost가 leaf 노드인 경우입니다.
두 상황 모두 동일하게 처리가 가능하며, 이는 removeRightMostElementOfLeftTree 메서드에서 살펴보겠습니다.
(rightMost의 right는 존재하면, 이는 rightMost가 아니었기 때문에 성립하지 않습니다.)
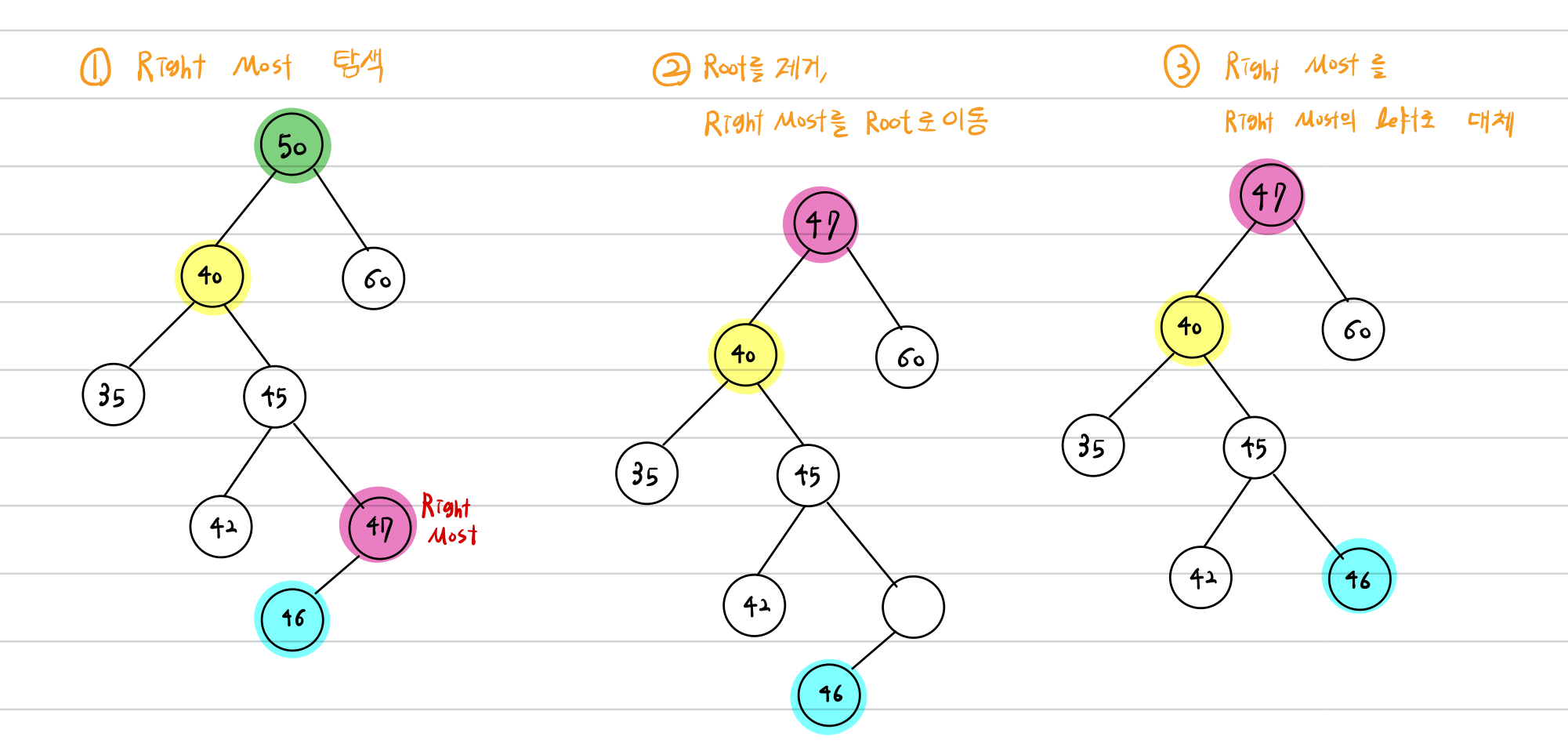
삭제 3 - removeRightMostElementOfLeftTree
private Key removeRightMostElementOfLeftTree(BinaryNode<Key> root) {
BinaryNode<Key> left = root.left();
if (!left.hasRight()) {
root.setLeft(left.left());
return left.element();
}
BinaryNode<Key> prev = left;
BinaryNode<Key> rightMost = left.right();
while (rightMost.hasRight()) {
prev = rightMost;
rightMost = rightMost.right();
}
prev.setRight(rightMost.left());
return rightMost.element();
}
설명
해당 메서드의 목적은 root로 들어온 노드의 좌측 서브트리에서 가장 큰 값(Right Most)을 찾아, 이를 제거함과 동시에 반환하는 것입니다.
Root로 들어온 노드의 left의 right가 존재하지 않는 경우와, 존재하는 경우를 나누어 확인하겠습니다.
1. Left의 Right가 존재하지 않는 경우
루트의 left를, left의 left로 설정해주면 됩니다.
이렇게 된다면 left의 left가 존재하지 않는다면 null이 세팅될 것이고, 존재한다면 존재하는 노드가 대입될 것이기에 문제되지 않습니다.
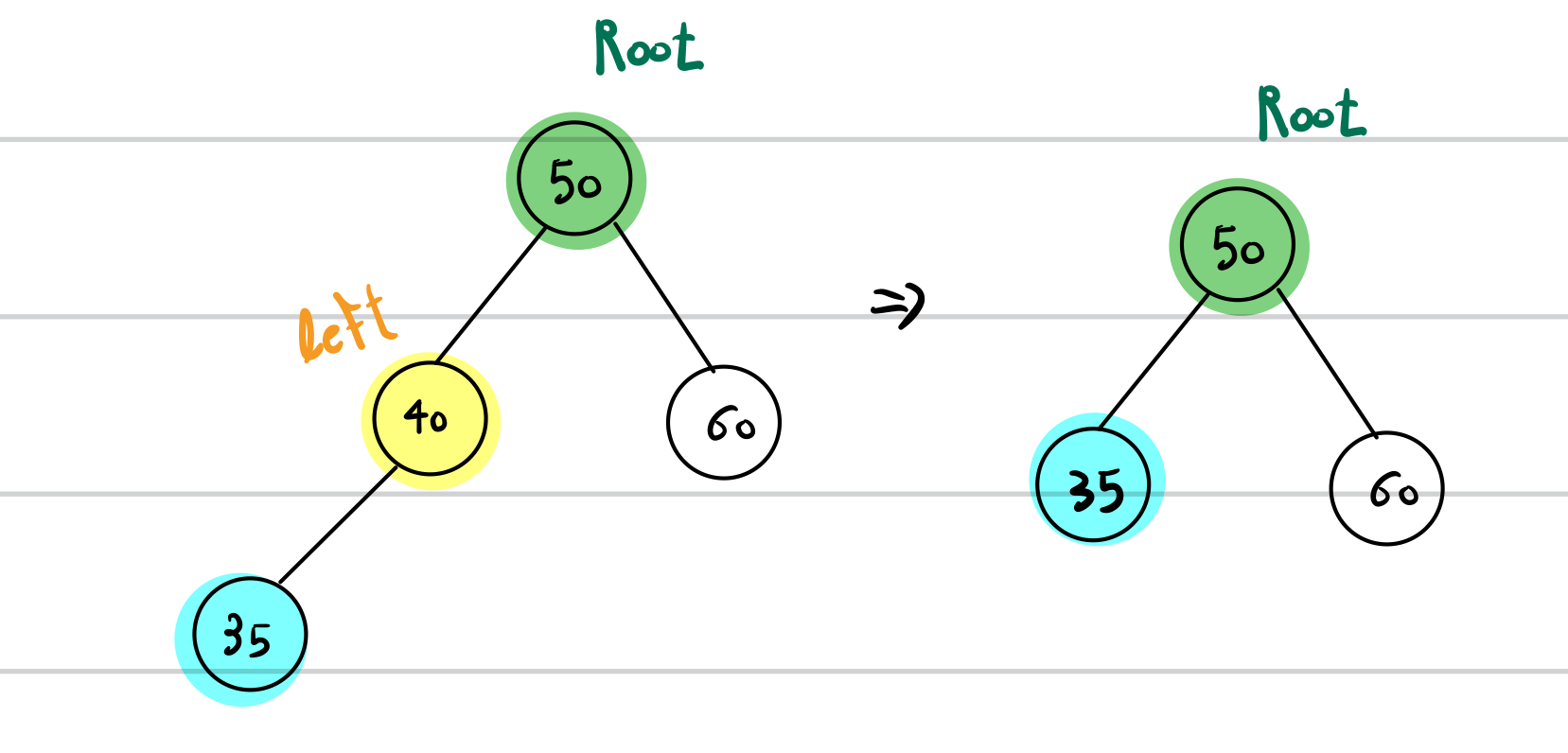
2. Left의 Right가 존재하는 경우
left를 prev, left의 right를 rightMost로 설정한 후 우측으로 계속 내려가는 작업을 수행합니다.
우측으로 내려갈 때마다 prev와 rightMost를 갱신해 주며,
rightMost의 right가 존재하지 않은 경우, 즉 rightMost라는 변수에 제대로 된 값이 할당된 경우 반복이 종료됩니다.
이 경우 prev의 right를, rightMost의 left를 통해 설정해준 뒤 rightMost의 값을 반환하면 제거가 완료됩니다.
rightMost의 left가 null인 경우에는 prev의 right에는 null이 설정될 것이고,
그렇지 않는 경우에는 존재하는 Node가 설정될 것이기에 올바르게 작동합니다.
삭제 4 - removeFromLeft
루트가 아닌 Left SubTree에서 값을 제거하는 경우에 대한 메서드입니다.
private Key removeFromLeft(Key key, BinaryNode<Key> root) {
if (! root.hasLeft()) {return null;}
BinaryNode<Key> leftChild = root.left();
int compareTo = key.compareTo(leftChild.element());
//== Key 가 더 큰 경우 ==//
if (compareTo > 0 ){return removeFromRight(key, leftChild);}
//== Key 가 더 작은 경우 ==//
if (compareTo < 0 ){return removeFromLeft(key, leftChild);}
//== 제거할 값을 찾은 경우==//
Key remove = leftChild.element();
if (leftChild.isLeaf()) {
root.setLeft(null);
}
if (leftChild.hasOneChild()){
if (leftChild.hasLeft()) {root.setLeft(leftChild.left());}
else if (leftChild.hasRight()) {root.setLeft(leftChild.right());}
}
//== 모두 존재하는 경우, left SubTree 에서 최댓값 제거한 후, 제거한 값을 요소로 세팅==//
else if (leftChild.hasTwoChild()) {leftChild.setElement(this.removeRightMostElementOfLeftTree(leftChild));}
this.size --;
return remove;
}우선 Root의 좌측 서브트리가 존재하지 않는다면 null을 반환합니다.
이후 Root의 left를 leftChild라 설정하였습니다.
이제 leftChild와 Key를 비교하여 다음 과정을 수행합니다.
1. Key가 더 크다면 해당 leftChild 노드를 루트로 하는 우측 서브트리에서 제거할 값을 찾습니다.
2. Key가 더 작다면 해당 leftChild 노드를 루트로 하는 좌측 서브트리에서 제거할 값을 찾습니다.
3. leftChild가 제거할 값과 동일하다면 다음 과정을 수행합니다.
3-1 : 만약 leftChild가 Leaf 노드라면 들어온 Root의 left를 Null로 바꾸어줍니다.
3-2 : 만약 leftChild의 자식이 1개만 존재한다면, root의 left를 해당 자식으로 바꾸어줍니다.
3-3 : 만약 leftChild의 자식이 2개 존재한다면, leftChild의 값을 leftChild의 좌측 서브트리의에서 가장 큰 값으로 변경한 후 제거해줍니다.
이는 제귀적으로 반복됩니다.
이제 leftChild와 Key가 동일한 상황에서 발생할 수 있는 3가지 상황에 대해 자세히 살펴보도록 하겠습니다.
모든 경우에서 LeftChild를 제거하는 것입니다.
1. leftChild가 Leaf 노드
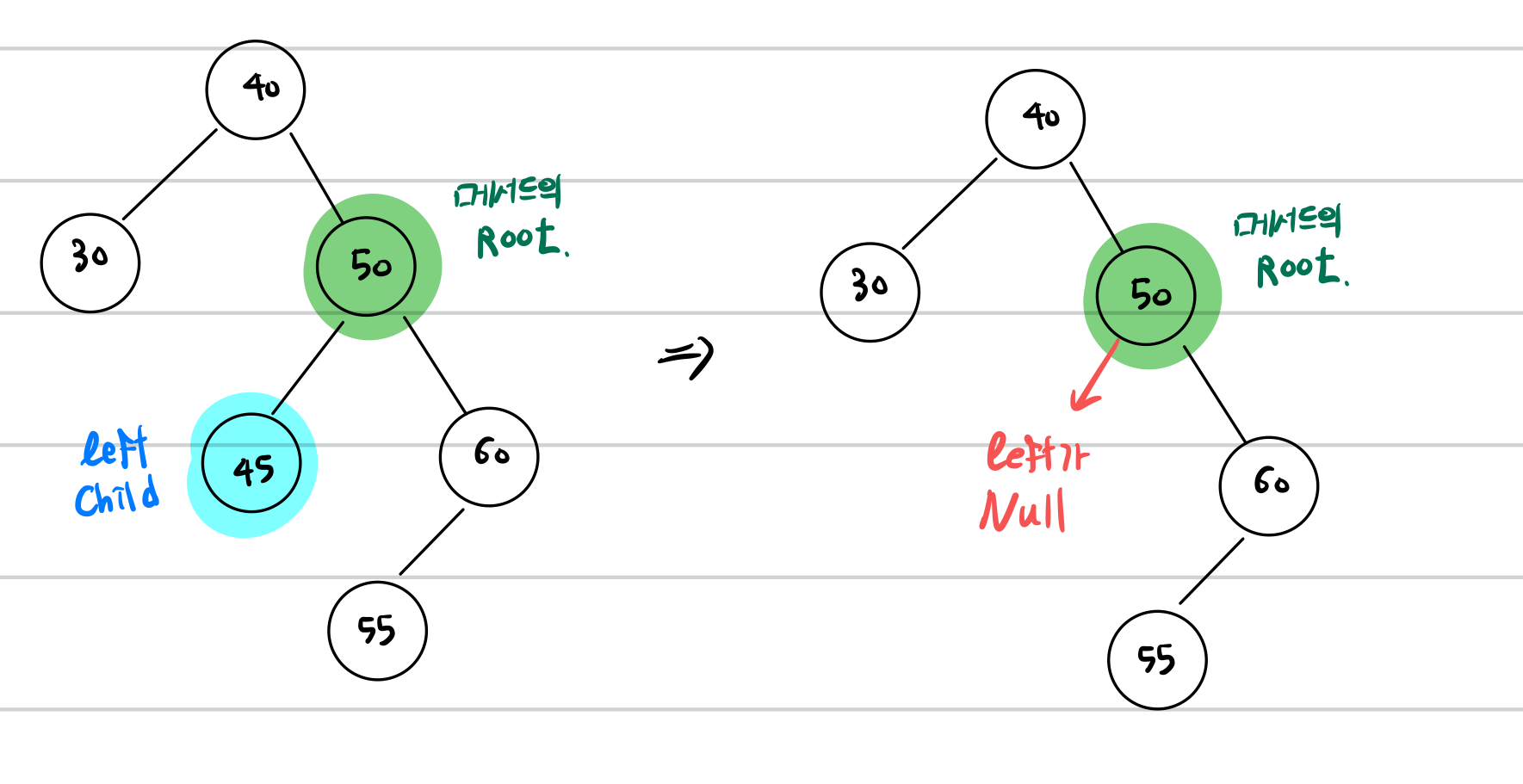
2. leftChild가 자식이 하나
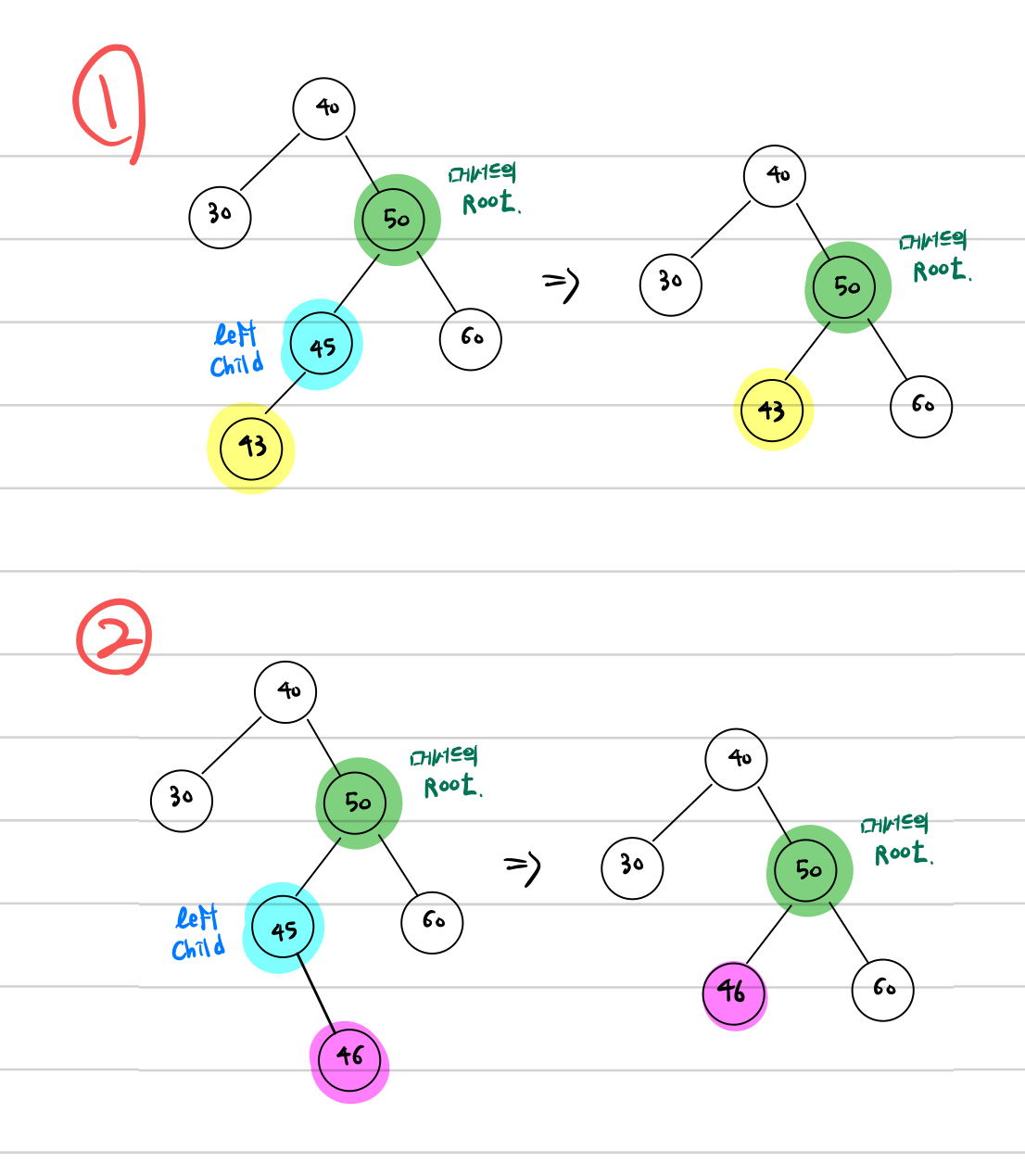
3. leftChild가 자식이 둘
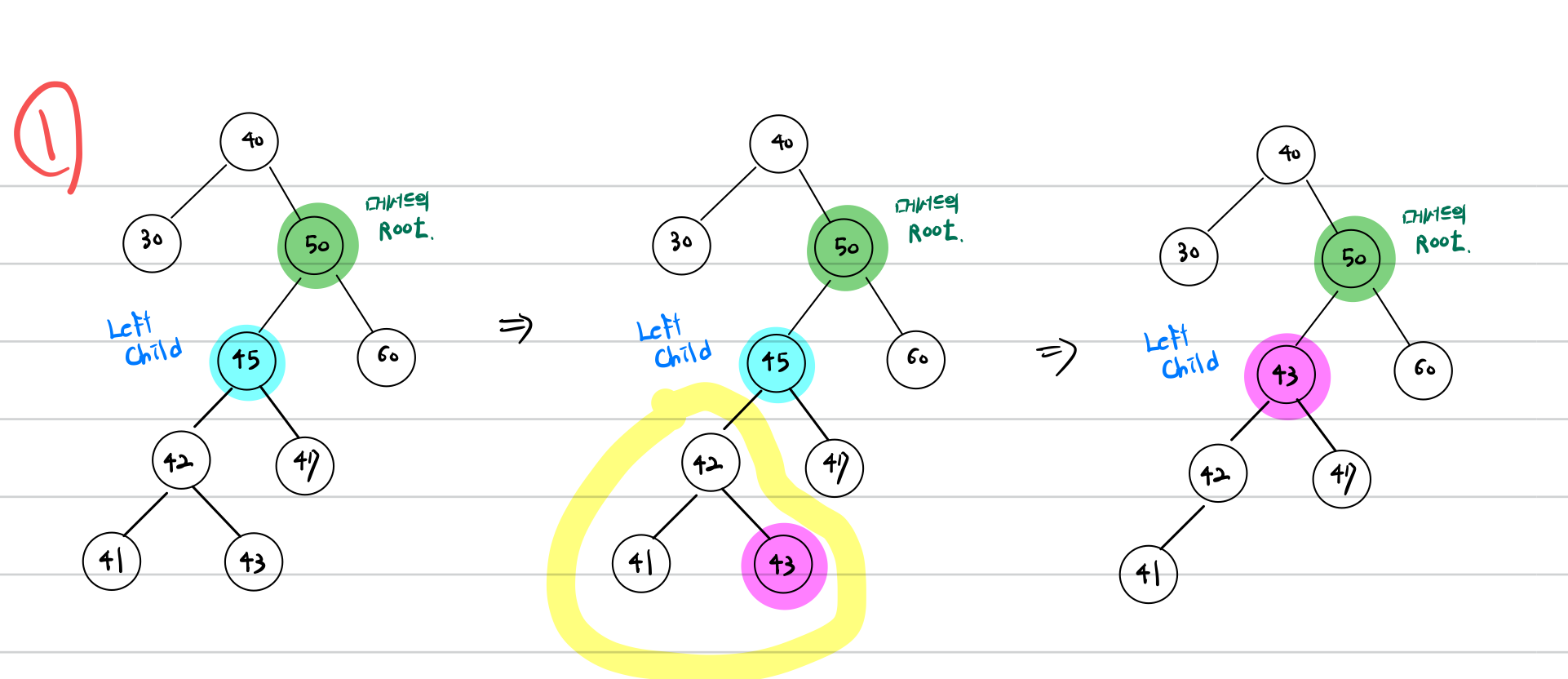
오름차순 출력 - inorder
@Override
public void inOrder() {
inOrderRecursive(this.root);
}
private void inOrderRecursive(BinaryNode<Key> root) {
if (root == null) return;
inOrderRecursive(root.left());
this.visit(root.element());
inOrderRecursive(root.right());
}BST에서 Inorder를 수행하면 오름차순으로 출력됩니다.
내림차순 출력 - reverseInorder
@Override
public void reverseInOrder() {
reverseInOrderRecursive(this.root);
}
private void reverseInOrderRecursive(BinaryNode<Key> root) {
if (root == null) return;
reverseInOrderRecursive(root.right());
this.visit(root.element());
reverseInOrderRecursive(root.left());
}BST에서 Inorder의 역과정을 수행하면 내림차순으로 출력됩니다.
전체 코드
public class BSTByLinkedNode <Key extends Comparable<Key>> implements BinarySearchTree<Key>{
private BinaryNode<Key> root;
private int size;
//== Getter / Setter ==//
public BinaryNode<Key> root() {
return root;
}
private void setRoot(BinaryNode<Key> root) {
this.root = root;
}
private void setSize(int size) {
this.size = size;
}
@Override
public boolean isEmpty() {
return this.size == 0;
}
@Override
public boolean isFull() {
return false;
}
@Override
public int size() {
return this.size;
}
@Override
public boolean contains(Key key) {
BinaryNode<Key> current = this.root;
while (current != null) {
int compareTo = key.compareTo(current.element());
//== Key 가 더 큰 경우 ==//
if (compareTo > 0) {current = current.right();}
//== Key 가 더 작은 경우 ==//
if (compareTo < 0) {current = current.left();}
//== 동일한 경우 ==//
if (compareTo == 0) {return true;}
}
return false;
}
@Override
public Key get(Key key) {
BinaryNode<Key> current = this.root;
while (current != null) {
int compareTo = key.compareTo(current.element());
//== Key 가 더 큰 경우 ==//
if (compareTo > 0) {current = current.right();}
//== Key 가 더 작은 경우 ==//
if (compareTo < 0) {current = current.left();}
//== 동일한 경우 ==//
if (compareTo == 0) {return current.element();}
}
return null;
}
@Override
public boolean add(Key key) {
BinaryNode<Key> addNode = new BinaryNode<>(key);
if(isEmpty()) {
setRoot(addNode);
this.size ++;
return true;
}
BinaryNode<Key> current = this.root;
while (current != null) {
int compareTo = key.compareTo(current.element());
//== Key 가 더 큰 경우 ==//
if (compareTo > 0) {
if (current.hasRight()) {current = current.right();}
else {
current.setRight(addNode);
break;
}
}
//== Key 가 더 작은 경우 ==//
if (compareTo < 0) {
if (current.hasLeft()) {current = current.left();}
else {
current.setLeft(addNode);
break;
}
}
//== 동일한 경우 -> 이미 존재하므로 삽입 실패 ==//
if (compareTo == 0) {
return false;
}
}
this.size++;
return true;
}
@Override
public Key remove(Key key) {
if (isEmpty()) return null;
int compareTo = key.compareTo(this.root.element());
if (compareTo == 0){
//== REMOVE ROOT !! ==//
return removeFromRoot();
}
return (compareTo > 0 )
? removeFromRight(key, this.root) //== Key 가 더 큰 경우 ==//
: removeFromLeft(key, this.root); //== Key 가 더 작은 경우 ==//
}
private Key removeFromRoot() {
Key remove = this.root.element();
if (root.isLeaf()) {
setRoot(null);
}//루트가 Leaf 인 경우 바로 제거
else if (root.hasOneChild()){//루트의 자식이 하나만 있는 경우
if (root.hasLeft()) {setRoot(this.root.left());} //Left 가 존재한다면 Root를 Root의 Left로 수정
else {setRoot(this.root.right());}//Right 가 존재한다면 Root를 Root의 Right로 수정
}
//== 모두 존재하는 경우, left SubTree 에서 최댓값 제거한 후, 제거한 값을 요소로 세팅==//
else if (root.hasTwoChild()) {root.setElement(this.removeRightMostElementOfLeftTree(root));}
this.size --;
return remove;
}
private Key removeRightMostElementOfLeftTree(BinaryNode<Key> root) {
BinaryNode<Key> left = root.left();
if (!left.hasRight()) {
root.setLeft(left.left());
return left.element();
}
BinaryNode<Key> prev = left;
BinaryNode<Key> rightMost = left.right();
while (rightMost.hasRight()) {
prev = rightMost;
rightMost = rightMost.right();
}
prev.setRight(rightMost.left());
return rightMost.element();
}
private Key removeFromLeft(Key key, BinaryNode<Key> root) {
if (! root.hasLeft()) {return null;}
BinaryNode<Key> leftChild = root.left();
int compareTo = key.compareTo(leftChild.element());
//== Key 가 더 큰 경우 ==//
if (compareTo > 0 ){return removeFromRight(key, leftChild);}
//== Key 가 더 작은 경우 ==//
if (compareTo < 0 ){return removeFromLeft(key, leftChild);}
//== 제거할 값을 찾은 경우==//
Key remove = leftChild.element();
if (leftChild.isLeaf()) {
root.setLeft(null);
}
if (leftChild.hasOneChild()){
if (leftChild.hasLeft()) {root.setLeft(leftChild.left());}
else if (leftChild.hasRight()) {root.setLeft(leftChild.right());}
}
//== 모두 존재하는 경우, left SubTree 에서 최댓값 제거한 후, 제거한 값을 요소로 세팅==//
else if (leftChild.hasTwoChild()) {leftChild.setElement(this.removeRightMostElementOfLeftTree(leftChild));}
this.size --;
return remove;
}
private Key removeFromRight(Key key, BinaryNode<Key> root) {
if (! root.hasRight()) {return null;}
BinaryNode<Key> rightChild = root.right();
int compareTo = key.compareTo(rightChild.element());
//== Key 가 더 큰 경우 ==//
if (compareTo > 0 ){return removeFromRight(key, rightChild);}
//== Key 가 더 작은 경우 ==//
if (compareTo < 0 ){return removeFromLeft(key, rightChild);}
//== 제거할 값을 찾은 경우==//
Key remove = rightChild.element();
if (rightChild.isLeaf()) {root.setRight(null);}
if (rightChild.hasOneChild()){
if (rightChild.hasLeft()) {root.setRight(rightChild.left());}
if (rightChild.hasRight()) {root.setRight(rightChild.right());}
}
//== 모두 존재하는 경우, left SubTree 에서 최댓값 제거한 후, 제거한 값을 요소로 세팅==//
if (rightChild.hasTwoChild()) {rightChild.setElement(this.removeRightMostElementOfLeftTree(rightChild));}
this.size --;
return remove;
}
@Override
public void inOrder() {
inOrderRecursive(this.root);
}
private void inOrderRecursive(BinaryNode<Key> root) {
if (root == null) return;
inOrderRecursive(root.left());
System.out.print( " -> " + root.element());
inOrderRecursive(root.right());
}
@Override
public void clear() {
this.size =0;
this.root = null;
}
}
테스트코드
public class Test {
public static void main(String[] args) {
BSTByLinkedNode<Integer> bst = new BSTByLinkedNode<>();
bst.add(40);
bst.add(20);
bst.add(60);
bst.add(10);
bst.add(30);
bst.add(50);
bst.add(70);
bst.add(45);
bst.add(55);
bst.add(52);
bst.inOrder();
System.out.println("");
System.out.println(" 삭제 ");
bst.remove(60);
bst.inOrder();
}
}
'☕️ Java > 자료구조 구현' 카테고리의 다른 글
| [Java] 자바로 Deap 구현하기 (0) | 2022.06.07 |
|---|---|
| [Java] 자바로 Heap 구현하기 (0) | 2022.06.06 |
| [Java] - 자바로 이진트리(Binary Tree) 구현하기 (0) | 2022.06.05 |
| [Java] - 자바로 Queue 구현하기 (노드 사용) (0) | 2022.06.04 |
| [Java] - 자바로 Circular Queue 구현하기 (1) | 2022.06.04 |