비결정성은 왜 쓰는가
비결정적 유한 인식기(nfa)는 결정적 유한 인식기(dfa)에 비해 모델링하기 쉬우며, 복잡한 문제를 간략하게 기술하는 데 효과적입니다.
또한 최적해를 찾기 위해 백트래킹(backtraking)등의 기법을 사용하여 모든 경우를 탐색했던 것을
최적의 선택을 할 수 있는 비결정적 알고리즘을 사용한다면 백트래킹 없이 문제를 해결할 수 있으며
결정적 알고리즘은 추가적인 작업을 통해서 비결정성을 시뮬레이트 할 수 있습니다.
이러한 이유로 비결정적 기계는 탐색 - 백트랙 알고리즘에 대한 모델로 사용될 수 있습니다.
또한 비결정성은 몇몇 복잡한 언어들을 간단하게 정의하는 데 효과적입니다.
예를 들어 다음과 같은 생성규칙
$$ S \to aSb | \lambda$$
은 모든 경우 두 생성규칙들 중 하나를 선택하게 되어 있음을 알 수 있습니다.
단지 두 개의 규칙만으로도 수많은 문자열들을 생성할 수 있게 해줍니다.
마지막으로, 비결정성을 도입하는 데에는 기술적인 이유가 존재합니다.
dfa보다는 nfa에 대한 어떤 이론적인 결과를 더 쉽게 수립할 수 있습니다.
nfa와 dfa, 이 두 가지 형태의 오토마타 사이에는 근본적인 차이가 없습니다.
따라서 비결정성을 사용함으로써 결론의 일반성을 그대로 유지하면서 공식적인 논증을 간단히 하는 효과를 누릴 수 있는 것입니다.
비결정성을 사용하는 이유에 대해 잠시 알아보았고, 이제 nfa를 dfa로 바꾸는 방법에 대해 알아보도록 하겠습니다.
결정적 유한 인식기와 비결정적 유한 인식기의 동치성
다음 조건이 만족되는 경우
$$L(M_1) = L(M_2)$$
즉 두 오토마타가 같은 언어를 인식하는 경우, 두 개의 유한 인식기 M1과 M2는 동치라 합니다.
일반적으로 주어진 언어를 인식하는 인식기들은 여러개가 존재할 수 있으며, 따라서 어느 dfa나 nfa든지 많은 동치인 인식기들이 있을 수 있습니다.
강력함(powerful)
한 종류의 오토마타가, 다른 종류의 오토마타에서 수행할 수 없는 어떤 일을 수행할 수 있음을 의미합니다.
dfa는 본질적으로 nfa의 한 제한된 종류이므로, dfa에 의해 인식되는 모든 언어는 어떤 nfa에 의해서도 인식될 수 있습니다.
그러나 그 역은 당연하다고 볼 수 없습니다.
nfa에는 비결정성이라는 개념이 추가되었고, 따라서 nfa에 의해 인식되면서 dfa로는 인식할 수 없는 언어가 존재하지 않을까 하고 생각할 수 있을 것입니다.
결론부터 말하자면, 이는 잘못된 생각입니다.
dfa들과 nfa는 똑같은 능력(equally powerful)을 가지고 있습니다.
즉 nfa에 의해 인식되는 모든 언어들에 대해 같은 언어를 인식하는 dfa가 항상 존재합니다.
증명은 너무 길어 생략하도록 하겠습니다.
정리
언어 L(M_N)을 비결정적 유한 인식기
$$M_N = (Q_N, \Sigma, \delta_N, q_0, F_N)$$
에 의해 인식되는 언어라 하면,
다음을 만족하는 결정적 유한 인식기는 반드시 존재합니다.
$$L(M_N) = L(M_D), \;\;\; M_D = (Q_D, \Sigma, \delta_D, \left\{q_0\right\}, F_D)$$
주어진 M(N)에 대하여, 이와 동치인 M(D)에 대한 전이 그래프 G(D)를 구성하기 위해
다음에서 소개하는 procedure nfa-to-dfa를 사용합니다.
이 때, G(D)의 모든 정점들은 정확히 |Σ| 개의 진출 간선들을 가져야 하며,
각 각선들은 Σ의 서로 다른 원소들을 라벨로 가져야 합니다.
procedure: nfa-to-dfa
1. 정점 {q_0}를 갖는 그래프 G(D)를 생성합니다. 이 정점은 초기 정점입니다.
2. 다음 과정을 모든 간선들이 생성될 때까지 반복합니다.
Σ의 원소 각각에 에 대해, 진출 간선을 갖지 않는 G(D)의 정점 {qi, qj, ..., qk}를 선택합니다.
다음을 계산합니다.
$${\delta}^{*}_N(q_i, a), \; {\delta}^{*}_N(q_j, a), ... , {\delta}^{*}_N(q_k, a) , \;\;\; 단, a \in \Sigma$$
$${\delta}^{*}_N(q_i, a) \cup {\delta}^{*}_N(q_j, a) \cup , ... \cup {\delta}^{*}_N(q_k, a) = \left\{ q_l, q_m, ... , q_n\right\}$$인 경우 G(D)에 라벨이 {ql, qm, ..., qn}인 정점이 아직 없다면, 이를 라벨로 갖는 정점을 추가합니다.
정점 {qi, qj, ..., qk}로부터 정점{ql, qm, ..., qn} 으로 향하는 간선을 추가하고 이에 라벨 a를 부여합니다.
3. G(D)의 상태들 중 라벨이 q(f)를 포함하는 모든 상태들을 승인 상태로 지정합니다.
$$단, \;\; q_f \in F_N$$
4. 인식기 M(N)이 λ를 인식하는 경우, G(D)의 정점 {q0}를 승인 정점으로 지정합니다
이 프로시저는 항상 종료함이 명백합니다.
단계 2의 반복작업이 한 번 수행될 때마다 G(D)에 간선이 하니씩 추가됩니다.
G(D)는 간선이 많아봤자 $$2^{|Q_N|}|\Sigma |$$개이므로, 이 반복잡업은 유한시간 내에 종료됩니다.
람다 클로저(lambda closure)
λ-closure(s)
상태 s에서 λ-transition만을 이용하여 도달 가능한 상태들의 집합을 의미합니다.(s도 포함합니다.)
$$\lambda-clusure(s) = \left\{ s \right\} \cup \left\{ q \; |\; \delta(p, \lambda) = q, \;\;p \in \lambda-closure(s) \right\} $$
$$\lambda-closure(T) = \cup_{S \in T} \lambda- closure(s)$$
T는 상태들의 집합이며, s는 T의 원소입니다.
설명:
상태 s에서 람다를 통해 도달한 여러 상태들과, 그러한 상태들에서 계속해서 람다를 통해 도달 가능한 모든 상태들의 집합을 의미합니다.
그리고 상태들의 집합 T 속에 존재하는 모든 원소들의 람다 클로져의 합집합을 T의 람다 클로져라 합니다.
Successor
a-successor(s)
상태 s에서 입력기호 a에 의해 도달 가능한 상태들의 집합을 의미합니다.
$$ a-successor(s) = \cup_{q_i \in T} \lambda-closure(\delta(q_i, a)) \;\; where\;\; T = \lambda-closure(s) $$
$$즉 \;\; T = \lambda-closure(s)$$
$$Ta = \delta(T, a) \;\;이며$$
$$a-successor(s) = \lambda-closure(Ta)$$
설명:
a-successor(s)는 s와, s에서 람다를 통해 이동 가능한 모든 상태들의 집합(즉 람다 클로저)에서 a를 입력하여 도달 가능한 상태들의 집합입니다.
이때 a를 입력하여 도달했음에도 람다 전이가 가능하다면, 결과에 포함됩니다.
아래 nfa를 예시로 설명해보겠습니다.
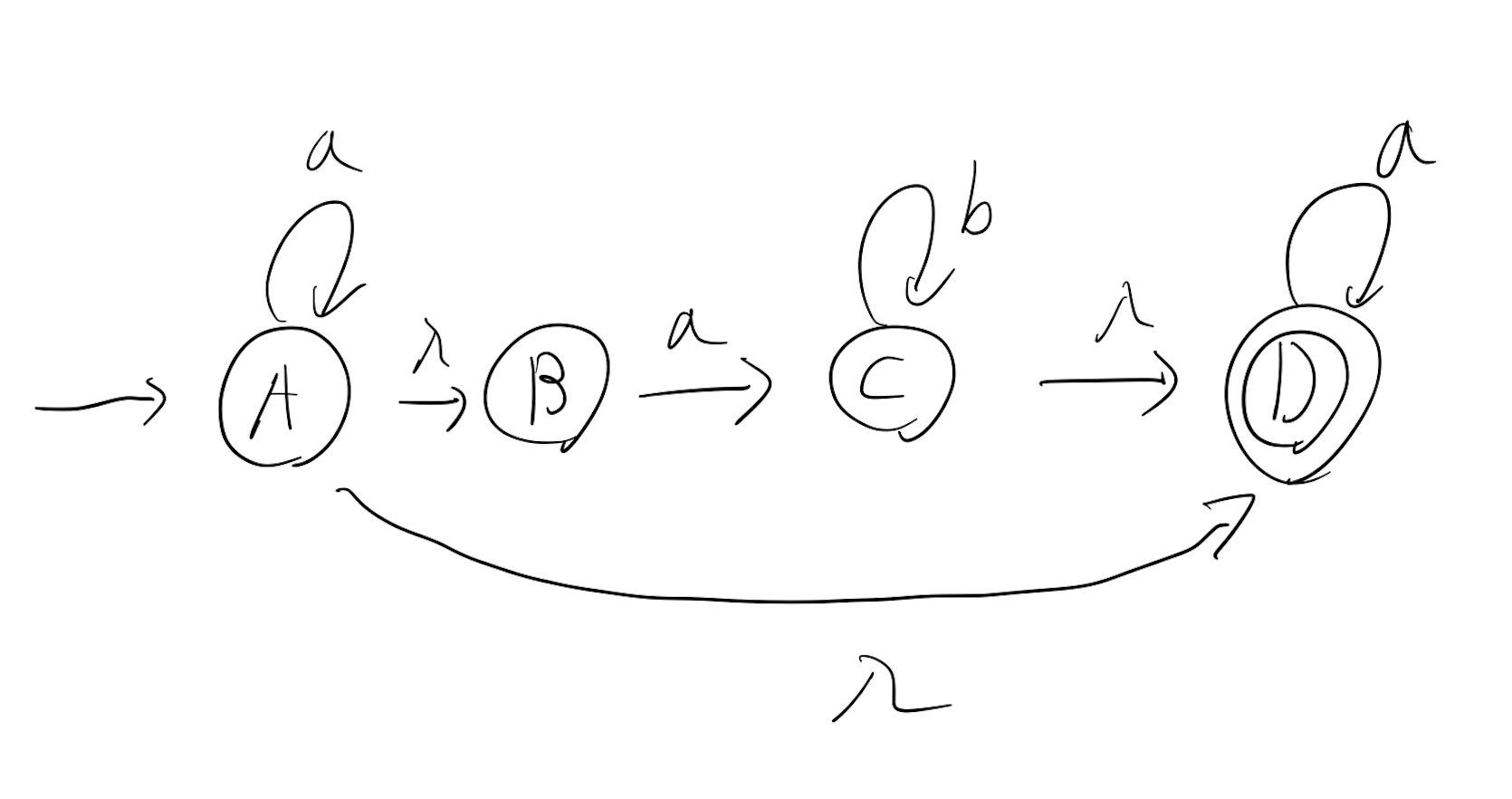
λ-closure(A)
$$\lambda-closure(A) = \left\{ A,B,D \right\}$$
$$\lambda-closure(\left\{ A, C \right\}) = \left\{ A,B,C, D \right\}$$
a-successor(A)
$$T = \lambda-closure(A) = \left\{ A,B,D \right\}$$
$$Ta = \delta(T, a) = \delta(A, a) \cup \delta(B,a) \cup \delta(D, a) = \left\{ A,C,D \right\}$$
$$\lambda-closure(Ta) = \lambda-closure(\left\{ A,C,D \right\}) = \left\{ A,B,C,D \right\}$$
$$따라서 \;\; a-successor(A) = \left\{ A,B,C,D \right\}$$
b-successor(C)
$$T = \lambda-closure(C) = \left\{ C,D \right\}$$
$$Tb = \delta(T, b) = \delta(C, b) \cup \delta(C,b)= \left\{ C \right\}$$
$$\lambda-closure(Tb) = \lambda-closure(\left\{ C \right\}) = \left\{ C,D \right\}$$
$$따라서\;\;b-successor(C) = \left\{ C,D \right\}$$
람다 클로저와 Successor를 사용하여 nfa를 dfa로 변환하기
이제 procedure: nfa-to-dfa의 과정에서, 람다 클로져와 successor를 사용하여 nfa를 dfa로 변환화는 방법을 살펴보도록 하겠습니다.
우선 초기 상태 q0에서의 람다 클로져를 모두 구한 뒤, 해당 집합을 A라 표현합니다.
모든 terminal symbol에 대한 successor(A), 즉 Σ-successor(A)를 구합니다.
이를 marking A라 칭합니다.
successor를 구하는 과정에서 새로운 집합이 등장하면, 이를 B, C, D, ...로 둡니다.
새로 등장한 집합에 대해 다시 Σ-successor(B), Σ-successor(C), ...즉 marking B, C, ... 를 구합니다.
이 과정을 반복한 후, 기존 nfa의 final state가 포함된 집합을 final state로 지정합니다.
위와 같은 nfa를 예시로 설명하겠습니다.
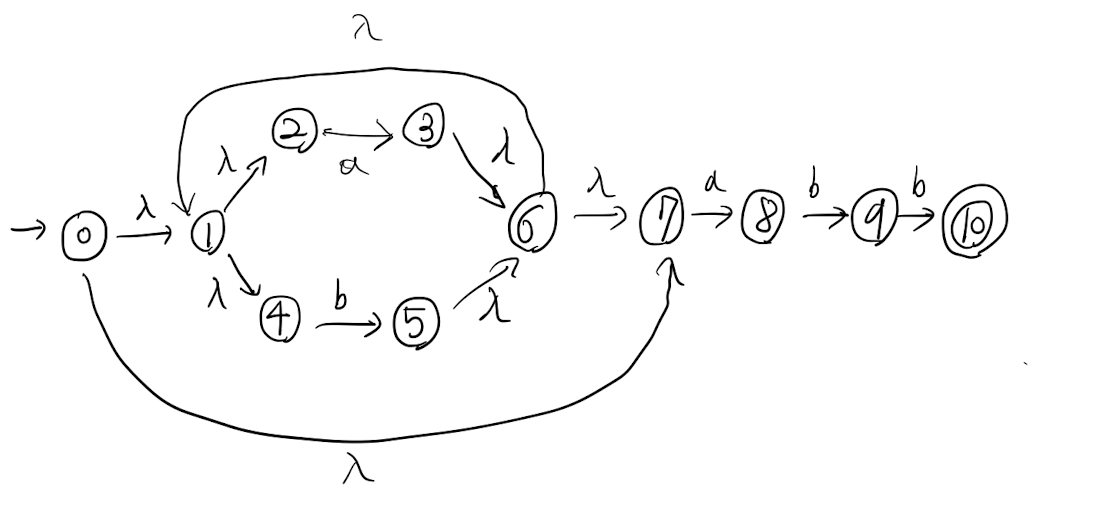
우선 초기상태 0에서의 람다 클로져를 모두 구하여 A 집합으로 설정하겠습니다.
$$\lambda-closure(0) = \left\{ 0,\;1,\;2,\;4,\;7 \right\} = A$$
marking A 과정을 진행합니다.
$$ a-successor(A) = \lambda-closure(\delta(\left\{ 0,\;1,\;2,\;4,\;7 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = \left\{ 1,\;2,\;3,\;4,\;6,\;7 \right\} = B$$
$$ b-successor(A) = \lambda-closure(\delta(\left\{ 0,\;1,\;2,\;4,\;7 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5 \right\}) = \left\{ 1,\;2,\;4,\;6,\;7 \right\} = C$$
위 과정에서 새롭게 등장한 B와 C에 대해 marking 작업을 수행합니다.
marking B 과정을 진행합니다.
$$ a-successor(B) = \lambda-closure(\delta(\left\{ 1,2,3,4,6,7,8 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = B$$
$$ b-successor(B) = \lambda-closure(\delta(\left\{ 1,2,3,4,6,7,8 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5, 9 \right\}) = \left\{ 1,2,4,5,6,7,9 \right\} = D$$
marking C 과정을 진행합니다.
$$ a-successor(C) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = B$$
$$ b-successor(C) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5 \right\}) = C\;\;\;$$
marking B 과정에서 새롭게 등장한 D에 대해 marking D 과정을 진행합니다.
$$ a-successor(D) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7,9 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = B$$
$$ b-successor(D) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7,9 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5,10 \right\}) = \left\{ 1,2,4,5,6,7,10 \right\} = E$$
marking D 과정에서 새롭게 등장한 E에 대해 marking E 과정을 진행합니다.
$$ a-successor(E) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7,10 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = B$$
$$ b-successor(E) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7,10 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5 \right\}) = C$$
이제 새롭게 등장한 상태가 없으므로 전이 그래프에 그려줍니다.
이때 final state는 기존 nfa의 final state인 10을 원소로 가지는 모든 상태가 되며, 이 경우에는 E가 final state가 됩니다.
유한 오토마타에서의 상태의 수 축소
어느 dfa나 유일하게 하나의 언어를 정의하게 됩니다.
하지만 그 역은 성립하지 않습니다.
즉 주어진 하나의 언어에 대해 이를 인식하는 dfa는 여러 개가 존재할 수 있는 것입니다.
서로 동치인(즉 같은 언어를 인식하는) 오토마타들에 대해서도, 각각의 오토마타들의 상태 수는 많은 차이가 날 수 있습니다.
계산을 목적으로 오토마타를 표현하고자 할 때, 상태의 수에 비례해서 기억 공간이 필요하게 됩니다.
기억 공간 효율성을 고려한다면 오토마타의 상태의 수를 가급적 줄이는 것이 바람직하며, 이를 위한 알고리즘을 알아보겠습니다.
구분가능(distinguishable)과 구분불가능(indistinguishable)
임의의 dfa에서의 두 상태 p와 q에 대해, 이들이 모든 문자열 $$w \in {\Sigma}^{*}$$
에 대해, 다음 조건을 만족하는 경우 이들을 구분불가능(indistinguishable)이라 합니다.
$$ {\delta}^{*}(p, w) \in F \;\; implies \;\; {\delta}(q, w) \in F $$
혹은
$$ {\delta}^{*}(p, w) \notin F \;\; implies \;\; {\delta}(q, w) \notin F $$
한편, 다음 조건을 만족하는 문자열 $$w \in {\Sigma}^{*}$$가 존재하는 경우, 상태 p와 q는 문자열 w에 의해 구분가능(distinguishable)이라 합니다
$$ {\delta}^{*}(p, w) \in F \;\; implies \;\; {\delta}(q, w) \notin F $$
또는
$$ {\delta}^{*}(p, w) \notin F \;\; implies \;\; {\delta}(q, w) \in F $$
구분불가능성의 동치관계
분명히 두 개의 상태는 서로 구분가능하거나 구분불가능할 것입니다.
구분불가능성은 동치관계(equivalence relation)의 성질을 가집니다.
상태 p와 q가 구분불가능이고, 상태 q와 r이 구분불가능이면, 상태 p와 r도 구분불가능입니다.
임의의 dfa에서 상태의 수를 줄이는 한 가지 방법은 구분불가능 상태들을 병합하는 것입니다
구분불가능한 상태들의 쌍을 찾아내는 방법은 procedure:mark라 부르며 다음과 같습니다.
procedure : mark
1. 모든 도달 불가능 상태들을 제거합니다.
이는 dfa의 그래프에서 초기 상태로부터의 모든 단순 경로들을 열거함으로써 수행할 수 있습니다.
해당 경로 상에 나타나지 않는다면 도달 불가능 상태인 것입니다.
2. 모든 상태 쌍 (p, q)에 대해 다음 경우를 만족하는 경우 (p, q)를 구분가능이라 마크합니다.
$$p \in F \;\; and \;\; q \notin F $$
$$또는, \;\; p \notin F \;\; and \;\; q \in F $$
3. 이전에 마크되지 않은 상태 쌍이 더 이상 마크되지 않을 때까지 다음 작업을 반복합니다.
모든 쌍 (p, q)와 모든 a∈Σ에 대하여 다음을 계산합니다.
$$\delta(p, a) = p_a \;\;와 \;\; \delta(q, a) = q_a $$
이때 (p(a), q(a))쌍이 구분가능으로 마크되어 있으면, (p, q)를 구분가능으로 마크합니다.
위의 프로시저가 모든 구분가능한 쌍들을 마크하는 알고리즘이 됩니다.
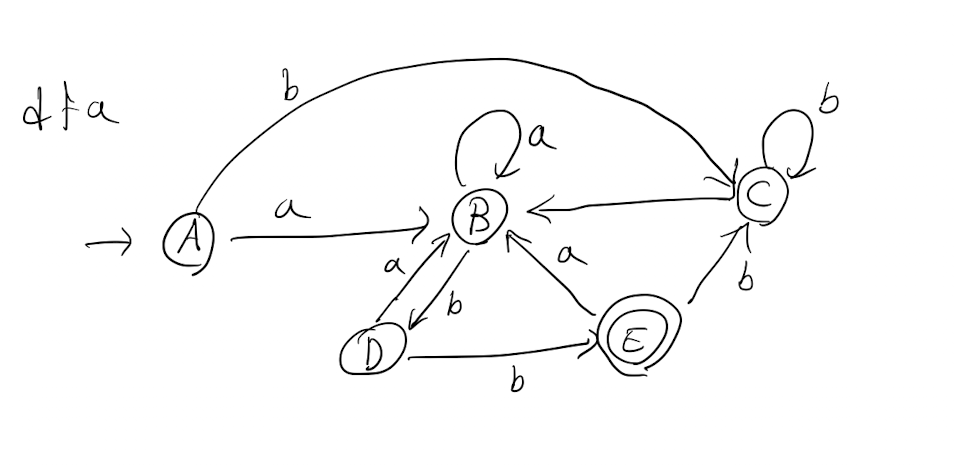
예시를 통해 살펴보겠습니다.
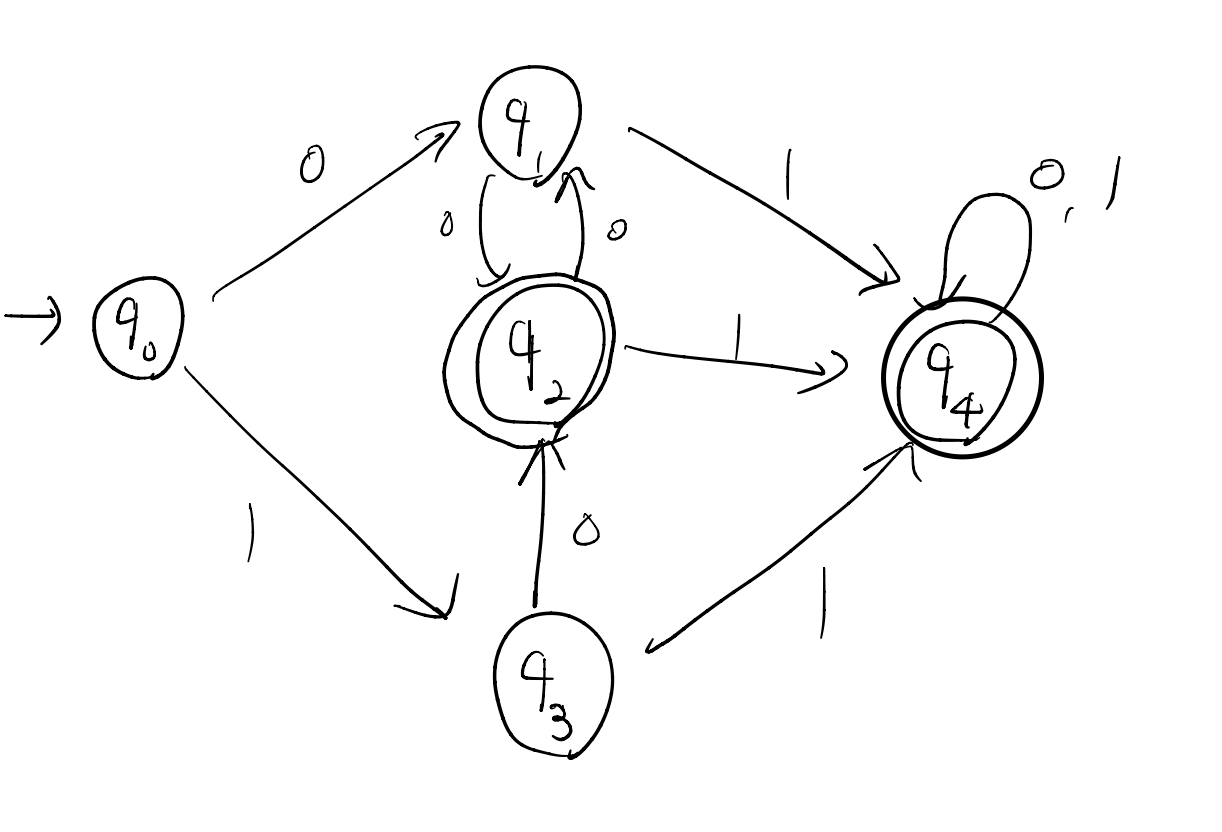
1. 도달 불가능 상태들은 존재하지 않습니다. 다음 단계로 넘어갑니다.
2. procedure :mark 의 2단계에서, 상태들의 집합을 승인 상태와 비승인 상태로 분할하여 다음 두 개의 동치 부류를 얻습니다.
$$\left\{q_0, q_1, q_3 \right\} \;과\; \left\{q_2, q_4 \right\}$$
3. procedure :mark 의 3단계를 진행합니다.
마크되지 않은 쌍 (q(0)과 q(1))에 대하여,
$$\delta(q_0, 0) = q_1\;\;\; 그리고 \;\;\; \delta(q_1, 0) = q_2$$
이므로 q(0)과 q(1)을 구분가능으로 마크합니다.
$$따라서, \;\; \left\{q_0, q_1, q_3 \right\}\;\;이\;\; \left\{q_0 \right\}, \;\;\; \left\{q_1, q_3 \right\} \;\; 으로 분리됩니다.$$
$$이때 \;\;\delta(q_1, 0) = q_2\;\;\; 그리고 \;\;\; \delta(q_3, 0) = q_2$$
$$\delta(q_1, 1) = q_4;\;\; 그리고 \;\;\; \delta(q_3, 1) = q_4$$
이므로 q(1)과 q(3)은 구분불가능입니다.
$$또한 \;\; \delta(q_2, 0) = q_1\;\;\; 그리고 \;\;\; \delta(q_4, 0) = q_4$$
이므로 q(2)과 q(4)을 구분가능으로 마크합니다.
위의 과정을 통해 구분불가능한 부류들이 확인되고 나면,
최소(minimal) dfa의 구성은 간단합니다.
다음 과정을 통해 최소 dfa를 구합니다.
procedure : reduce
주어진 오토마타
$$M = (Q, \Sigma, \delta, q_0, F)$$
에 대해, 다음과 같은 절차에 따라 축소된 DFA를 구성합니다.
$$축소된\; dfa \;\; \hat{M} = (\hat{Q}, \Sigma, \hat{\delta}, \hat{q_0}, \hat{F})$$
1. 프로시저 mark를 사용하여 동치 부류들을 생성합니다.
즉 위에서 했었던 과정을 통해 동치 부류들을 찾아내는 것입니다.
2.
$$구분불가능한 \;\;상태들의\;\; 집합\;\; \left\{q_i, q_j, ..., q_k \right\}\;\;의 \;각각의 \;원소들에\; 대하여$$
$$라벨이\; ij...k\;인 \;\; \hat{M}\;의 \;상태(state)\;를 \;생성합니다.$$
3.
다음 형태를 갖는 M의 각 전이 규칙에 대하여
$$\delta(q_r, a) = q_p$$
qr과 qp가 속한 집합을 찾아냅니다.
$$만일 \;\; q_r \in \left\{ q_i, q_j, .., q_k \right\}\;\;이고$$
$$q_p \in \left\{ q_l, q_m, .., q_n \right\} \;\; 이라면 \;\; \hat{\delta}에 \;\; 아래 \;규칙을\; 추가합니다$$
$$\hat{\delta}(ij...k, a) = lm...n$$
4. $$초기 \;상태\; \hat{q_0}은\;\; \hat{M}의\; 상태들 \; 중\; 라벨이 \; 0을\; 포함하는\; 상태입니다$$
5.$$\hat{F}는 \; 라벨이 \; q_i \in F \;인 \;i를 \;포함하는 \; 모든\; 상태들의 \; 집합으로 \; 합니다.$$
'🖥 Computer Science > 계산이론' 카테고리의 다른 글
| [계산이론] - (5) 정규 표현 (Regular Expression) (0) | 2022.05.04 |
|---|---|
| [계산이론] - (4) 밀리기계(Mealy Machine), 무어기계(Moore Machine) (0) | 2022.04.25 |
| [계산이론] - (2) 유한 오토마타 (Finite Automata) : DFA, NFA (0) | 2022.04.15 |
| [계산이론] - (1) 언어, 문법, 오토마타 (1) | 2022.04.06 |
| [계산이론] -기본 지식(3) : 그래프와 트리 (0) | 2022.03.19 |
비결정성은 왜 쓰는가
비결정적 유한 인식기(nfa)는 결정적 유한 인식기(dfa)에 비해 모델링하기 쉬우며, 복잡한 문제를 간략하게 기술하는 데 효과적입니다.
또한 최적해를 찾기 위해 백트래킹(backtraking)등의 기법을 사용하여 모든 경우를 탐색했던 것을
최적의 선택을 할 수 있는 비결정적 알고리즘을 사용한다면 백트래킹 없이 문제를 해결할 수 있으며
결정적 알고리즘은 추가적인 작업을 통해서 비결정성을 시뮬레이트 할 수 있습니다.
이러한 이유로 비결정적 기계는 탐색 - 백트랙 알고리즘에 대한 모델로 사용될 수 있습니다.
또한 비결정성은 몇몇 복잡한 언어들을 간단하게 정의하는 데 효과적입니다.
예를 들어 다음과 같은 생성규칙
$$ S \to aSb | \lambda$$
은 모든 경우 두 생성규칙들 중 하나를 선택하게 되어 있음을 알 수 있습니다.
단지 두 개의 규칙만으로도 수많은 문자열들을 생성할 수 있게 해줍니다.
마지막으로, 비결정성을 도입하는 데에는 기술적인 이유가 존재합니다.
dfa보다는 nfa에 대한 어떤 이론적인 결과를 더 쉽게 수립할 수 있습니다.
nfa와 dfa, 이 두 가지 형태의 오토마타 사이에는 근본적인 차이가 없습니다.
따라서 비결정성을 사용함으로써 결론의 일반성을 그대로 유지하면서 공식적인 논증을 간단히 하는 효과를 누릴 수 있는 것입니다.
비결정성을 사용하는 이유에 대해 잠시 알아보았고, 이제 nfa를 dfa로 바꾸는 방법에 대해 알아보도록 하겠습니다.
결정적 유한 인식기와 비결정적 유한 인식기의 동치성
다음 조건이 만족되는 경우
$$L(M_1) = L(M_2)$$
즉 두 오토마타가 같은 언어를 인식하는 경우, 두 개의 유한 인식기 M1과 M2는 동치라 합니다.
일반적으로 주어진 언어를 인식하는 인식기들은 여러개가 존재할 수 있으며, 따라서 어느 dfa나 nfa든지 많은 동치인 인식기들이 있을 수 있습니다.
강력함(powerful)
한 종류의 오토마타가, 다른 종류의 오토마타에서 수행할 수 없는 어떤 일을 수행할 수 있음을 의미합니다.
dfa는 본질적으로 nfa의 한 제한된 종류이므로, dfa에 의해 인식되는 모든 언어는 어떤 nfa에 의해서도 인식될 수 있습니다.
그러나 그 역은 당연하다고 볼 수 없습니다.
nfa에는 비결정성이라는 개념이 추가되었고, 따라서 nfa에 의해 인식되면서 dfa로는 인식할 수 없는 언어가 존재하지 않을까 하고 생각할 수 있을 것입니다.
결론부터 말하자면, 이는 잘못된 생각입니다.
dfa들과 nfa는 똑같은 능력(equally powerful)을 가지고 있습니다.
즉 nfa에 의해 인식되는 모든 언어들에 대해 같은 언어를 인식하는 dfa가 항상 존재합니다.
증명은 너무 길어 생략하도록 하겠습니다.
정리
언어 L(M_N)을 비결정적 유한 인식기
$$M_N = (Q_N, \Sigma, \delta_N, q_0, F_N)$$
에 의해 인식되는 언어라 하면,
다음을 만족하는 결정적 유한 인식기는 반드시 존재합니다.
$$L(M_N) = L(M_D), \;\;\; M_D = (Q_D, \Sigma, \delta_D, \left\{q_0\right\}, F_D)$$
주어진 M(N)에 대하여, 이와 동치인 M(D)에 대한 전이 그래프 G(D)를 구성하기 위해
다음에서 소개하는 procedure nfa-to-dfa를 사용합니다.
이 때, G(D)의 모든 정점들은 정확히 |Σ| 개의 진출 간선들을 가져야 하며,
각 각선들은 Σ의 서로 다른 원소들을 라벨로 가져야 합니다.
procedure: nfa-to-dfa
1. 정점 {q_0}를 갖는 그래프 G(D)를 생성합니다. 이 정점은 초기 정점입니다.
2. 다음 과정을 모든 간선들이 생성될 때까지 반복합니다.
Σ의 원소 각각에 에 대해, 진출 간선을 갖지 않는 G(D)의 정점 {qi, qj, ..., qk}를 선택합니다.
다음을 계산합니다.
$${\delta}^{*}_N(q_i, a), \; {\delta}^{*}_N(q_j, a), ... , {\delta}^{*}_N(q_k, a) , \;\;\; 단, a \in \Sigma$$
$${\delta}^{*}_N(q_i, a) \cup {\delta}^{*}_N(q_j, a) \cup , ... \cup {\delta}^{*}_N(q_k, a) = \left\{ q_l, q_m, ... , q_n\right\}$$인 경우 G(D)에 라벨이 {ql, qm, ..., qn}인 정점이 아직 없다면, 이를 라벨로 갖는 정점을 추가합니다.
정점 {qi, qj, ..., qk}로부터 정점{ql, qm, ..., qn} 으로 향하는 간선을 추가하고 이에 라벨 a를 부여합니다.
3. G(D)의 상태들 중 라벨이 q(f)를 포함하는 모든 상태들을 승인 상태로 지정합니다.
$$단, \;\; q_f \in F_N$$
4. 인식기 M(N)이 λ를 인식하는 경우, G(D)의 정점 {q0}를 승인 정점으로 지정합니다
이 프로시저는 항상 종료함이 명백합니다.
단계 2의 반복작업이 한 번 수행될 때마다 G(D)에 간선이 하니씩 추가됩니다.
G(D)는 간선이 많아봤자 $$2^{|Q_N|}|\Sigma |$$개이므로, 이 반복잡업은 유한시간 내에 종료됩니다.
람다 클로저(lambda closure)
λ-closure(s)
상태 s에서 λ-transition만을 이용하여 도달 가능한 상태들의 집합을 의미합니다.(s도 포함합니다.)
$$\lambda-clusure(s) = \left\{ s \right\} \cup \left\{ q \; |\; \delta(p, \lambda) = q, \;\;p \in \lambda-closure(s) \right\} $$
$$\lambda-closure(T) = \cup_{S \in T} \lambda- closure(s)$$
T는 상태들의 집합이며, s는 T의 원소입니다.
설명:
상태 s에서 람다를 통해 도달한 여러 상태들과, 그러한 상태들에서 계속해서 람다를 통해 도달 가능한 모든 상태들의 집합을 의미합니다.
그리고 상태들의 집합 T 속에 존재하는 모든 원소들의 람다 클로져의 합집합을 T의 람다 클로져라 합니다.
Successor
a-successor(s)
상태 s에서 입력기호 a에 의해 도달 가능한 상태들의 집합을 의미합니다.
$$ a-successor(s) = \cup_{q_i \in T} \lambda-closure(\delta(q_i, a)) \;\; where\;\; T = \lambda-closure(s) $$
$$즉 \;\; T = \lambda-closure(s)$$
$$Ta = \delta(T, a) \;\;이며$$
$$a-successor(s) = \lambda-closure(Ta)$$
설명:
a-successor(s)는 s와, s에서 람다를 통해 이동 가능한 모든 상태들의 집합(즉 람다 클로저)에서 a를 입력하여 도달 가능한 상태들의 집합입니다.
이때 a를 입력하여 도달했음에도 람다 전이가 가능하다면, 결과에 포함됩니다.
아래 nfa를 예시로 설명해보겠습니다.

λ-closure(A)
$$\lambda-closure(A) = \left\{ A,B,D \right\}$$
$$\lambda-closure(\left\{ A, C \right\}) = \left\{ A,B,C, D \right\}$$
a-successor(A)
$$T = \lambda-closure(A) = \left\{ A,B,D \right\}$$
$$Ta = \delta(T, a) = \delta(A, a) \cup \delta(B,a) \cup \delta(D, a) = \left\{ A,C,D \right\}$$
$$\lambda-closure(Ta) = \lambda-closure(\left\{ A,C,D \right\}) = \left\{ A,B,C,D \right\}$$
$$따라서 \;\; a-successor(A) = \left\{ A,B,C,D \right\}$$
b-successor(C)
$$T = \lambda-closure(C) = \left\{ C,D \right\}$$
$$Tb = \delta(T, b) = \delta(C, b) \cup \delta(C,b)= \left\{ C \right\}$$
$$\lambda-closure(Tb) = \lambda-closure(\left\{ C \right\}) = \left\{ C,D \right\}$$
$$따라서\;\;b-successor(C) = \left\{ C,D \right\}$$
람다 클로저와 Successor를 사용하여 nfa를 dfa로 변환하기
이제 procedure: nfa-to-dfa의 과정에서, 람다 클로져와 successor를 사용하여 nfa를 dfa로 변환화는 방법을 살펴보도록 하겠습니다.
우선 초기 상태 q0에서의 람다 클로져를 모두 구한 뒤, 해당 집합을 A라 표현합니다.
모든 terminal symbol에 대한 successor(A), 즉 Σ-successor(A)를 구합니다.
이를 marking A라 칭합니다.
successor를 구하는 과정에서 새로운 집합이 등장하면, 이를 B, C, D, ...로 둡니다.
새로 등장한 집합에 대해 다시 Σ-successor(B), Σ-successor(C), ...즉 marking B, C, ... 를 구합니다.
이 과정을 반복한 후, 기존 nfa의 final state가 포함된 집합을 final state로 지정합니다.
위와 같은 nfa를 예시로 설명하겠습니다.

우선 초기상태 0에서의 람다 클로져를 모두 구하여 A 집합으로 설정하겠습니다.
$$\lambda-closure(0) = \left\{ 0,\;1,\;2,\;4,\;7 \right\} = A$$
marking A 과정을 진행합니다.
$$ a-successor(A) = \lambda-closure(\delta(\left\{ 0,\;1,\;2,\;4,\;7 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = \left\{ 1,\;2,\;3,\;4,\;6,\;7 \right\} = B$$
$$ b-successor(A) = \lambda-closure(\delta(\left\{ 0,\;1,\;2,\;4,\;7 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5 \right\}) = \left\{ 1,\;2,\;4,\;6,\;7 \right\} = C$$
위 과정에서 새롭게 등장한 B와 C에 대해 marking 작업을 수행합니다.
marking B 과정을 진행합니다.
$$ a-successor(B) = \lambda-closure(\delta(\left\{ 1,2,3,4,6,7,8 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = B$$
$$ b-successor(B) = \lambda-closure(\delta(\left\{ 1,2,3,4,6,7,8 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5, 9 \right\}) = \left\{ 1,2,4,5,6,7,9 \right\} = D$$
marking C 과정을 진행합니다.
$$ a-successor(C) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = B$$
$$ b-successor(C) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5 \right\}) = C\;\;\;$$
marking B 과정에서 새롭게 등장한 D에 대해 marking D 과정을 진행합니다.
$$ a-successor(D) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7,9 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = B$$
$$ b-successor(D) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7,9 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5,10 \right\}) = \left\{ 1,2,4,5,6,7,10 \right\} = E$$
marking D 과정에서 새롭게 등장한 E에 대해 marking E 과정을 진행합니다.
$$ a-successor(E) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7,10 \right\} , \;a\;)) \; = \lambda-closure(\left\{ 3,8 \right\}) = B$$
$$ b-successor(E) = \lambda-closure(\delta(\left\{ 1,2,4,5,6,7,10 \right\} , \;b\;)) \; = \lambda-closure(\left\{ 5 \right\}) = C$$
이제 새롭게 등장한 상태가 없으므로 전이 그래프에 그려줍니다.
이때 final state는 기존 nfa의 final state인 10을 원소로 가지는 모든 상태가 되며, 이 경우에는 E가 final state가 됩니다.

유한 오토마타에서의 상태의 수 축소
어느 dfa나 유일하게 하나의 언어를 정의하게 됩니다.
하지만 그 역은 성립하지 않습니다.
즉 주어진 하나의 언어에 대해 이를 인식하는 dfa는 여러 개가 존재할 수 있는 것입니다.
서로 동치인(즉 같은 언어를 인식하는) 오토마타들에 대해서도, 각각의 오토마타들의 상태 수는 많은 차이가 날 수 있습니다.
계산을 목적으로 오토마타를 표현하고자 할 때, 상태의 수에 비례해서 기억 공간이 필요하게 됩니다.
기억 공간 효율성을 고려한다면 오토마타의 상태의 수를 가급적 줄이는 것이 바람직하며, 이를 위한 알고리즘을 알아보겠습니다.
구분가능(distinguishable)과 구분불가능(indistinguishable)
임의의 dfa에서의 두 상태 p와 q에 대해, 이들이 모든 문자열 $$w \in {\Sigma}^{*}$$
에 대해, 다음 조건을 만족하는 경우 이들을 구분불가능(indistinguishable)이라 합니다.
$$ {\delta}^{*}(p, w) \in F \;\; implies \;\; {\delta}(q, w) \in F $$
혹은
$$ {\delta}^{*}(p, w) \notin F \;\; implies \;\; {\delta}(q, w) \notin F $$
한편, 다음 조건을 만족하는 문자열 $$w \in {\Sigma}^{*}$$가 존재하는 경우, 상태 p와 q는 문자열 w에 의해 구분가능(distinguishable)이라 합니다
$$ {\delta}^{*}(p, w) \in F \;\; implies \;\; {\delta}(q, w) \notin F $$
또는
$$ {\delta}^{*}(p, w) \notin F \;\; implies \;\; {\delta}(q, w) \in F $$
구분불가능성의 동치관계
분명히 두 개의 상태는 서로 구분가능하거나 구분불가능할 것입니다.
구분불가능성은 동치관계(equivalence relation)의 성질을 가집니다.
상태 p와 q가 구분불가능이고, 상태 q와 r이 구분불가능이면, 상태 p와 r도 구분불가능입니다.
임의의 dfa에서 상태의 수를 줄이는 한 가지 방법은 구분불가능 상태들을 병합하는 것입니다
구분불가능한 상태들의 쌍을 찾아내는 방법은 procedure:mark라 부르며 다음과 같습니다.
procedure : mark
1. 모든 도달 불가능 상태들을 제거합니다.
이는 dfa의 그래프에서 초기 상태로부터의 모든 단순 경로들을 열거함으로써 수행할 수 있습니다.
해당 경로 상에 나타나지 않는다면 도달 불가능 상태인 것입니다.
2. 모든 상태 쌍 (p, q)에 대해 다음 경우를 만족하는 경우 (p, q)를 구분가능이라 마크합니다.
$$p \in F \;\; and \;\; q \notin F $$
$$또는, \;\; p \notin F \;\; and \;\; q \in F $$
3. 이전에 마크되지 않은 상태 쌍이 더 이상 마크되지 않을 때까지 다음 작업을 반복합니다.
모든 쌍 (p, q)와 모든 a∈Σ에 대하여 다음을 계산합니다.
$$\delta(p, a) = p_a \;\;와 \;\; \delta(q, a) = q_a $$
이때 (p(a), q(a))쌍이 구분가능으로 마크되어 있으면, (p, q)를 구분가능으로 마크합니다.
위의 프로시저가 모든 구분가능한 쌍들을 마크하는 알고리즘이 됩니다.
예시를 통해 살펴보겠습니다.

1. 도달 불가능 상태들은 존재하지 않습니다. 다음 단계로 넘어갑니다.
2. procedure :mark 의 2단계에서, 상태들의 집합을 승인 상태와 비승인 상태로 분할하여 다음 두 개의 동치 부류를 얻습니다.
$$\left\{q_0, q_1, q_3 \right\} \;과\; \left\{q_2, q_4 \right\}$$
3. procedure :mark 의 3단계를 진행합니다.
마크되지 않은 쌍 (q(0)과 q(1))에 대하여,
$$\delta(q_0, 0) = q_1\;\;\; 그리고 \;\;\; \delta(q_1, 0) = q_2$$
이므로 q(0)과 q(1)을 구분가능으로 마크합니다.
$$따라서, \;\; \left\{q_0, q_1, q_3 \right\}\;\;이\;\; \left\{q_0 \right\}, \;\;\; \left\{q_1, q_3 \right\} \;\; 으로 분리됩니다.$$
$$이때 \;\;\delta(q_1, 0) = q_2\;\;\; 그리고 \;\;\; \delta(q_3, 0) = q_2$$
$$\delta(q_1, 1) = q_4;\;\; 그리고 \;\;\; \delta(q_3, 1) = q_4$$
이므로 q(1)과 q(3)은 구분불가능입니다.
$$또한 \;\; \delta(q_2, 0) = q_1\;\;\; 그리고 \;\;\; \delta(q_4, 0) = q_4$$
이므로 q(2)과 q(4)을 구분가능으로 마크합니다.
위의 과정을 통해 구분불가능한 부류들이 확인되고 나면,
최소(minimal) dfa의 구성은 간단합니다.
다음 과정을 통해 최소 dfa를 구합니다.
procedure : reduce
주어진 오토마타
$$M = (Q, \Sigma, \delta, q_0, F)$$
에 대해, 다음과 같은 절차에 따라 축소된 DFA를 구성합니다.
$$축소된\; dfa \;\; \hat{M} = (\hat{Q}, \Sigma, \hat{\delta}, \hat{q_0}, \hat{F})$$
1. 프로시저 mark를 사용하여 동치 부류들을 생성합니다.
즉 위에서 했었던 과정을 통해 동치 부류들을 찾아내는 것입니다.
2.
$$구분불가능한 \;\;상태들의\;\; 집합\;\; \left\{q_i, q_j, ..., q_k \right\}\;\;의 \;각각의 \;원소들에\; 대하여$$
$$라벨이\; ij...k\;인 \;\; \hat{M}\;의 \;상태(state)\;를 \;생성합니다.$$
3.
다음 형태를 갖는 M의 각 전이 규칙에 대하여
$$\delta(q_r, a) = q_p$$
qr과 qp가 속한 집합을 찾아냅니다.
$$만일 \;\; q_r \in \left\{ q_i, q_j, .., q_k \right\}\;\;이고$$
$$q_p \in \left\{ q_l, q_m, .., q_n \right\} \;\; 이라면 \;\; \hat{\delta}에 \;\; 아래 \;규칙을\; 추가합니다$$
$$\hat{\delta}(ij...k, a) = lm...n$$
4. $$초기 \;상태\; \hat{q_0}은\;\; \hat{M}의\; 상태들 \; 중\; 라벨이 \; 0을\; 포함하는\; 상태입니다$$
5.$$\hat{F}는 \; 라벨이 \; q_i \in F \;인 \;i를 \;포함하는 \; 모든\; 상태들의 \; 집합으로 \; 합니다.$$
'🖥 Computer Science > 계산이론' 카테고리의 다른 글
| [계산이론] - (5) 정규 표현 (Regular Expression) (0) | 2022.05.04 |
|---|---|
| [계산이론] - (4) 밀리기계(Mealy Machine), 무어기계(Moore Machine) (0) | 2022.04.25 |
| [계산이론] - (2) 유한 오토마타 (Finite Automata) : DFA, NFA (0) | 2022.04.15 |
| [계산이론] - (1) 언어, 문법, 오토마타 (1) | 2022.04.06 |
| [계산이론] -기본 지식(3) : 그래프와 트리 (0) | 2022.03.19 |
