서론
https://ttl-blog.tistory.com/562?category=926966
[계산이론] - 언어, 문법, 오토마타
언어 (Languages) 우리들은 이미 자연 언어(natural languages)를 사용하고 있으며, 이러한 개념과는 친숙합니다. 그러나 "언어"라는 단어에 대해서 설명을 하라고 한다면, 이는 생각보다 어려울 것입니
ttl-blog.tistory.com
해당 포스팅의 마지막에서 촘스키 계층에 대해 조금 살펴보았습니다.
촘스키 계층에는 무제한(unrestricted) 문법, 문맥연관(context-sensitive) 문법, 문맥자유(context-free) 문법, 정규(regular) 문법이 있었습니다.
이번 포스팅에서부터 저희는 정규 문법에 의해 생성되는 언어인 정규 언어에 대해 공부할 것입니다.
다음은 정규 언어를 표현하기 위한 세 가지의 방법입니다.
정규 표현(regular expression)
정규 문법(regular grammer)
유한 오토마타 (dfa 혹은 nfa)
정규 표현(regular expression)
$\Sigma$ 를 주어진 알파벳이라 하면, 정규 표현은 아래와 같습니다.
1. $\phi, \; \lambda,\; a \in \Sigma $ 는 모두 정규 표현입니다.
이들을 기본 정규 표현(primitive regular expression)이라 합니다.
2.$ r_1$ 과 $r_2$ 가 정규 표현이면, 다음 식 모두 다 정규 표현입니다.
$$r_1 + r_2 , \;\; r_1 \cdot r_2, \;\; r_1 ^{*}, \;\; (r_1)$$
3. 특정 문자열이 정규 표현이 되기 위해서는 기본 정규 표현에서 시작하여 (2)번의 규칙을 유한 횟수만큼 반복함으로써 해당 문자열이 유도될 수 있어야 합니다.
예시
정규 표현에 의해 묘사되는 언어
위에서 배운 정규 표현이 표현하는 언어에 대해서 알아보도록 하겠습니다.
임의의 정규 표현 r에 대해, L(r)이 r과 관련된 언어를 나타낸다고 하면, 정규표현 r에 의해 묘사되는 언어 L(r)은 다음 규칙들에 의해 정의됩니다.
1. $\phi$ 은 공집합 $\left\{ \right\}$ 을 나타내는 정규 표현입니다.
2. $\lambda$는 $\left\{ \lambda \right\}$를 나타내는 정규 표현입니다.
3. 모든 $a \in \Sigma$에 대해, $a$ 는 $\left\{ a\right\}$를 나타내는 정규 표현입니다.
4. 만일 $r_1$과 $r_2$가 정규 표현일 경우, 다음이 성립합니다.
$$L(r_1 + r_2 ) = L(r_1) \cup L(r_2)$$
$$L(r_1 \cdot r_2 ) = L(r_1)L(r_2)$$
$$L((r_1)) = L(r_1)$$
$$L(r_1^{*} ) = (L(r_1))^{*}$$
해당 정의의 마지막 4개 규칙들은 $L(r)$ 을 보다 간단한 형태의 구성 요소로 변환하는 작업을 재귀적으로 계속 진행하기 위해 사용되며, 첫 3개의 규칙들은 이러한 재귀를 종료하기 위해 사용됩니다.
아래 4개의 수식들을 적용할 때, 우선순위가 존재하며, 다음과 같습니다.
$$*> \cdot> +$$
(스타폐포 > 접합 > 합집합 순서입니다.)
(이때 접합 연산자는 기호의 생략이 가능합니다.)
예시





연습문제






형식 언어는 다양한 2차원 형상을 묘사하는 목적으로 사용될 수 있다.
체인-코드 언어는 알파벳 $\Sigma = \left\{ u,d,r,l \right\}$ 기반으로 정의되며, 여기서 각 문자가 갖는 의미는 다음과 같다.
u : 위를 향하는 단위 길이를 갖는 직선
d : 아래를 향하는 단위 길이를 갖는 직선
r : 오른쪽을 향하는 단위 길이를 갖는 직선
l : 왼쪽을 향하는 단위 길이를 갖는 직선

유용한 정규 표현
$$(a+b)(a+b) = (a+b)^{2} \to \left\{ w : |w| =2 \; , w\in \left\{ a,b\right\}^{*} \right\}$$
$$((a+b)^{2})^{*} \to \left\{ w : |w| \;mod \;2 = 0 \; , w\in \left\{ a,b\right\}^{*} \right\}$$
$$((a+b)^{3})^{*}(a+b) \to \left\{ w : |w| \;mod \;3 = 1 \; , w\in \left\{ a,b\right\}^{*} \right\}$$
$$ a^{*}b \to \left\{ a^{n} b : n \geq 0 \right\} $$
$$ a(a+b)^{*}a \to \left\{ awa : w\in \left\{ a,b\right\}^{*} \right\} $$
$$ a^{*}b^{*} \to \left\{ a^{n}b^{m} : n \geq 0 , m \geq 0 \right\} $$
$$ (ab)^{*} \to \left\{ (ab)^{n} : n \geq 0 \right\} $$
$$ a(a+b)^{*}aa(a+b)^{*}a \to \left\{ aw_1aaw_2a : w_1, w_2 \in \left\{ a,b\right\}^{*} \right\} $$
정규 표현의 항등 관계
$$r\lambda = \lambda r = r$$
$$ a\cdot a^{*} = a^{*}\cdot a$$
$$ (r^{*})^{*} = r^{*}$$
$$(rs)^{*}r = r(sr)^{*}$$
$$(r^{*} + s^{*})^{*} = (r+s)^{*}$$
$$(r^{*}s^{*})^{*} = (r+s)^{*}$$
$$r^{*}(sr^{*})^{*} = (r^{*}s)^{*}r^{*} = (r+s)^{*}$$
동치 관계(equivalence relation)
두 개의 정규 표현이 같은 언어를 묘사하는 경우 이들을 서로 동치라 합니다.
정규 표현 $\to$ 유한 오토마타
dfa에 의해 인식되는 언어를 정규 언어라고 합니다.
정규 표현은 정규 언어를 표현하기 위한 한가지 수단이므로, 이 말은 정규 표현이 표현하는 언어는 정규 언어라는 뜻입니다.
따라서 정규 표현으로 표현되는 언어를 accept하는 nfa도 존재합니다.
이제부터 정규 표현에 대한 nfa를 만드는 방법을 알아보겠습니다.
주어진 정규 표현 r에 대해 $L(r)$ 을 인식하는 nfa를 구성할 수 있으며, 다음은 기본 정규 표현에 대한 nfa입니다.

그리고 정규 표현의 연산들에 대한 nfa입니다.

결론적으로 r이 정규 표현일 경우
위의 nfa들을 사용하여 주어진 정규 표현 r에 대해 L(r)을 인식하는 nfa를 구성할 수 있으며
이에 동치인 dfa는 항상 존재하므로 L(r)은 정규 언어 입니다.
예시
유한 오토마타 $\to$ 정규 표현
위와는 반대로 정규 언어 혹은 nfa가 주어졌을 때 이를 표현하는 정규 표현을 만드는 방법을 알아보겠습니다.
1. 정규 언어를 nfa로 바꿉니다.
2. nfa의 초기 상태로부터 승인 상태까지의 모든 보행에 대한 라벨들을 포함하는 정규 표현을 찾아야 합니다.
이때 2번 과정을 어려운 일은 아니지만 전이 그래프에서는 사이클들이 존재하고
이들이 임의의 순서로 몇 번이나 순회할 지 모르기에 조금 복잡합니다.
위 문제를 해결하기 위해 직관적인 방법 중 하나는 일반 전이 그래프(generalized transition graph, GTG)라 불리는 우회 기법을 사용하는 것입니다.
여기서만 제한적으로 사용되며, 이후에는 사용되지 않으므로 간단하게 언급하고 넘어가겠습니다.
일반 전이 그래프 (GTG)
간선의 라벨에 정규 표현을 부여하는 전이 그래프
일반 전이 그래프(GTG)에서 초기 상태로부터 승인 상태까지의 임의의 보행에 대한 라벨은 여러 정규 표현들의 접합이 되며, 따라서 그 자체도 정규표현이 됩니다.

그러한 정규 표현들이 묘사하는 문자열들은 해당 일반 전이 그래프에 의하여 인식되는 언어의 부분집합이 되며,
이와 같이 생성되는 모든 부분집합들의 합집합이 해당 언어가 됩니다.
임의의 nfa에 대한 그래프는 간선의 라벨을 적당히 해석할 수만 있다면 일반 전이 그래프로 볼 수 있습니다.
예를 들어 단일 문자 a를 라벨로 갖는 간선은, 정규 표현 a를 라벨로 갖는 것으로 해석할 수 있습니다.
여러 문자 a,b,c,...를 라벨로 갖는 간선은 정규표현 a+b+c+...을 라벨로 갖는 것으로 해석할 수 있습니다.
즉, 모든 정규 언어에 대해 이를 인식하는 일반 전이 그래프가 존재합니다.
역으로 일반 전이 그래프에 의해 인식되는 언어도 모두 정규 언어가 됩니다.
complete GTG(완전 GTG)
완전 GTG는 GTG 중 모든 간선을 포함하는 그래프입니다.
만일 nfa로부터 변환된 GTG에 몇몇 간선이 존재하지 않을 경우, 그 간선들을 추가하고 Φ를 라벨로 주면 됩니다.

$|V|$ 개의 정점을 갖는 완전 GTG 그래프는 정확히 $|V|^{2}$ 개 만큼의 간선을 갖습니다.
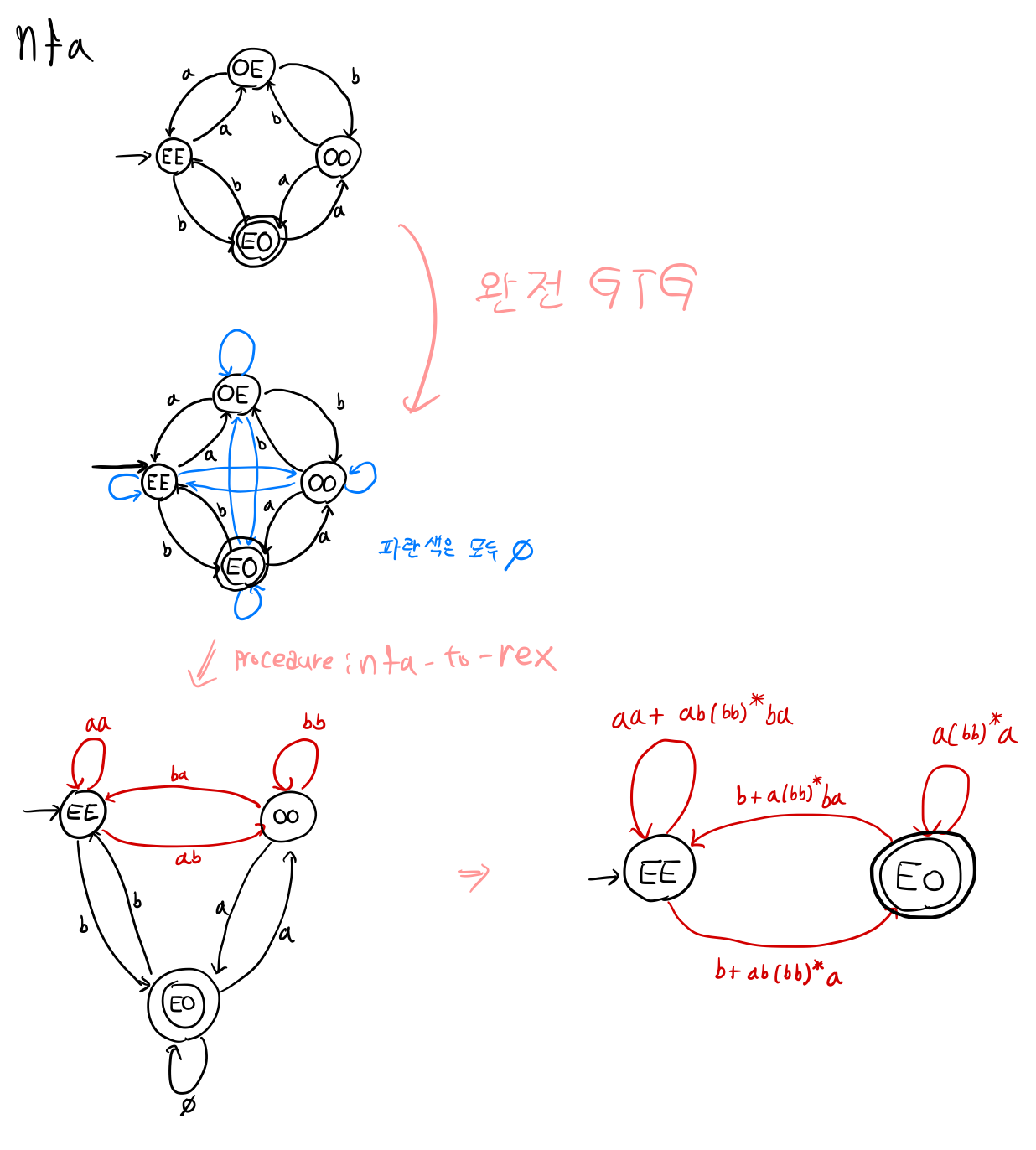
procedure: nfa-to-rex (nfa를 정규 표현으로 바꾸기)
1. 상태가 $q_0, q_1, ..., q_n$ 이고 승인 상태가 하나인 nfa로부터 시작합니다.
2. nfa를 완전 GTG로 변환합니다. 이때 $r_{ik}$ 가 $q_i$ 에서 $q_k$ 로의 간선의 라벨을 나타낸다고 하겠습니다.
3. GTG가 만약 오직 두 개의 상태 $q_i$와 $q_k$를 가지며, 여기서 $q_i$ 가 초기 상태, $q_k$ 를 승인 상태라 할 때, 이 GTG와 연관된 정규 표현은 다음과 같습니다.
$$r = r_{ii}^{*}r_{ik}(r_{kk} + r_{ki}r^{*}_{ii}r_{ik})^{*}$$
예시

4. GTG가 만약 3개의 상태 $q_i$ 와 $q_k$ , $q_h$ 를 가지며, 여기서 $q_i$ 가 초기 상태, $q_k$ 를 승인 상태, $q_h$ 를 제 3의 상태라 할 때, 다음과 같은 라벨을 갖는 새로운 간선들을 추가합니다.
$$ r_{pq} + r_{ph}r^{*}_{hh}r_{hq}, \;\;\; p = i, k, \;\; q = i,k $$
그러고 나서 정점 $q_i$ 와 그에 연결된 간선들을 제거합니다.
예시
5. 만약 GTG가 4개 이상의 상태를 가지고 있다면, 제거할 상태 $q_k$ 를 선택합니다.
모든 상태들의 쌍 $(q_i, q_k)$ 에, 규칙 4를 적용합니다.
각 단계에서, 가능한 경우 아래와 같은 단순화 하는 규칙을 적용합니다.
$$r + \phi = r$$
$$r\phi = \phi$$
$$\phi^{*} = \lambda$$
이후 정점 $q_k$ 와 그것과 연결된 간선들을 제거합니다.
6. 올바른 정규 표현을 얻을 때까지 단계 3에서 5까지 반복합니다
위 과정을 통해 저희는 아래와 같은 정리를 얻을 수 있습니다.
L을 정규 언어라 하면, $L = L(r)$ 을 만족하는 정규 표현 r이 존재합니다.
언어 L이 정규 언어라면, 그에 대한 nfa가 존재합니다.
일반성을 잃지 않고 이 nfa가 승인 상태를 하나만 가지고 있다고 가정할 수 있습니다.
이 nfa에 대해 프로시저 nfa-to-rex를 적용하면 원하는 정규 표현을 얻을 수 있습니다.
예시
다음 언어에 대한 정규 표현을 찾아보겠습니다.
$$L = \left\{ w \in \left\{ a,b \right\}^{*} : n_a(w)는\;\; 짝수이고\;\; n_b(w)는\;\;홀수이다 \right\}$$
연습문제






'🖥 Computer Science > 계산이론' 카테고리의 다른 글
| [계산이론] - (7) 정규 언어의 폐포(Closure) 성질 (0) | 2022.05.11 |
|---|---|
| [계산이론] - (6) 정규 문법(regular grammer) (2) | 2022.05.11 |
| [계산이론] - (4) 밀리기계(Mealy Machine), 무어기계(Moore Machine) (0) | 2022.04.25 |
| [계산이론] - (3) NFA에서의 DFA로의 변환방법 (0) | 2022.04.24 |
| [계산이론] - (2) 유한 오토마타 (Finite Automata) : DFA, NFA (0) | 2022.04.15 |


